STATISTIK-FORUM.de

[Tranbaer44]

Hallo ihr Lieben,

Ich bin noch recht neu in der Welt der Statistik und ich hoffe, dass diese Frage nicht zu sehr in Richtung Absatz 5 in den Richtlinen (Hausarbeiten) fällt...

Ich habe die erste Aufgabe welche ich der "Poisson Verteilung" zugeordnet habe mit Ach und Krach lösen können.

Aufgabe 1. In einem Naturschutzgebiet sichtet man durchschnittlich drei Bären wöchentlich. Wie groß ist die Wahrscheinlichkeit von (a) genau zwei Sichtungen, (b) mehr als vier Sichtungen.

a.) (Lamda) = 3

P (X=2) = 3^2/2 +e^-3 =0,2240 bzw im Excel X =2 Mittelwert = 3 Kumuliert = 0 (Ich weiß Excel ist nicht so praktisch für statistische Berechnungen, aber ich bin noch recht neu in der Materie und taste mich erst an "R" ran )

b.)

P (X=>4) = 1-P (X <_ 4) = 1-( 3^0/0 * e^-3 + 3^1/1*e^-3+3^2/2*e^-3+ 3^3/3*e^-3+ 3^4/4 *e^-3)

= 1-16,375 * e^-3 =0.1847 bzw im Excel X =4 Mittelwert = 3 Kumuliert = 1 1-0,815263245 = 0.1847


Nun zu meiner Frage. Ich hoffe ihr könnt mir da weiterhelfen.

Bei diesem Beispiel wollte ich ähnlich vorgehen jedoch habe ich hier eine weitere Komponente mit Zeiteinheiten dabei und schaue leider ins Leere...

Aufgabe 2)

Eine EDV Hotline wird durchschnittlich 24mal pro Stunde kontaktiert. Mit welcher Wahrscheinlichkeit erhält die Hotline
a.) in den nächsten 10 Minuten keinen Anruf,
b) innerhalb von 15 Minuten höchstens vier Anrufe, sowie
c) innerhalb von zwanzig Minuten höchstens sechs Anrufe?

Ich habe versucht die Anrufe Pro Minute zu eruieren und bin auf 0,4 gekommen.

bei a.) müsste ich dann laut Adam Riese ja P (X=0) haben oder? Aber wie baue ich die Minuten dann in meine Formel ein?

Ich erwarte mir bei Gott nicht, dass sich jetzt jemand die Zeit nimmt und mir die gesamte Formel aufschreibt, da mir das ja nix bringt um es zu verstehen, aber es wäre sehr nett, wenn mir jemand helfen könnte auf den richtigen Weg zu kommen um diese Aufgabe selbst lösen zu können. Ich steh leider echt an...

[bele]

Hi!

Klar ist das ein Absatz 5 Fall und Du verhälst Dich genauso, wie es in Absatz 5 erbeten wird. Also kein Problem. Außer vielleicht, dass es hier nicht um Statistik, sondern um Stochastik geht, aber so kleinlich sind wir auch wieder nicht.

Aus der Wikipedia kopiere ich:


Damit ist die wesentliche Formel aufgeschrieben.

Für Aufgabe 2 schlage ich vor, dass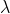 für 10 Minuten zu errechnen. Gegeben ist das 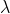für 1 Stunde. Du könntest es mit einem sogenannten "Dreisatz" versuchen: Wenn eine Hotline in 1 Stunde durchschnittlich 24 Mal angerufen wird, wie häufig wird sie durchschnittlich in 10 Minunten angerufen?

Kannst Du die Aufgabe so lösen?

LG,
Bernhard

[Tranbaer44]

Danke mal vorab für die Antwort lieber Bernhard,

Ich bin mir nicht ganz sicher.

Bin so an die Sache herangegangen.

0,4 Anrufe /min
-->
4 Anrufe /10min

P(x=0) = 4^0/0*e^-4 = 0,018315 im Excel POISSON(0;4;0) für X;Mittelwert;Kumuliert

und für die weiteren Unterbeispiele nehm ich dann einfach für b.) Lamda 6 (für 15 min) und 4 für k
und bei c) Lamda 8 (für 20 min) und 6 für k

hoffe ich bin da auf der richtigen Fährte. Das einzige was mich stutzig macht ist das mit "höchstens", weil ich die neuen Daten, welche ich gerade ermittelt habe, ja dann nicht eins zu eins in die Formel eintragen kann.

Meines Erachtens kommt da nämlich eine viel zu kleine Prozentzahl heraus. Ich bin wirklich kein Profi in Umgang mit Zahlen....

[bele]

P(x=0) = 4^0/0*e^-4 = 0,018315

Du willst aber nicht wirklich durch Null teilen! Wenn Dir die Werte nicht plausibel erscheinen, dann rechne noch mal von Hand ohne kummulierende Excel-Funktion nach.

LG,
Bernhard

[Tranbaer44]

War ein Denkfehler meinerseits. Meinte natürlich 0! was ja 1 ist und nicht 0:-P

Konnte die Aufgabe dann ohne weitere Probleme lösen. Vielen Dank nochmal