Hallo,
ich habe eigentlich was Ingenieurswissenschaftliches studiert, interessiere mich aber auch für Statistik und habe nebenher einige Online-Kurse zur statistischen Datenanalyse mit R gemacht.
Leider passen aber die dort behandelten Beispiele oft nicht so richtig auf meine Anwendungsfälle und dann bin ich unsicher, wie ich vorgehen muss. Bei meinem derzeitigen Projekt geht es um eine Anlage, bei der zu Beginn ein Bauteil gefehlt hat. Dadurch hat die Anlage pro Tag sehr oft getaktet (ca. 35 mal), das wurde bemerkt und das Bauteil nachgerüstet. Eine gewisse (geringere!) Taktung ist normal, aber eben nicht so oft.
Nun würde ich gerne wissen, ob ich langfristig an der Anzahl der Taktungen pro Tag erkennen kann, ob das Bauteil verschleißt, denn dann würde diese Anzahl wieder langsam hochgehen.
Ich habe Daten über 63 Tage, an denen die Anlage lief und die korrekte Funktion des Bauteils manuell überwacht wurde. Meist taktet die Anlage 8 mal pro Tag, allerdings mit leichter Streuung, die durch äußere Faktoren bedingt ist, die wir nicht beeinflussen können:
https://seafile.rlp.net/f/58be93cd46e342ad8fad/?dl=1
Ich würde nun gerne automatisiert die Anzahl der Taktungen überwachen lassen und eine Fehlermeldung bekommen, wenn diese sich signifikant erhöht. Also z. B. wenn ich mit 90 %-iger Wahrscheinlichkeit davon ausgehen kann, dass die inzwischen gemessenen Taktungen nicht mehr im "normalen" Bereich liegen.
Muss ich da jetzt mit der Poisson-Verteilung rangehen? Ich bin unsicher, da mein Erwartungswert ja erstens nicht genau 8 ist und ich aus meinen 63 Referenztagen auch eine Verteilung habe, die ja nicht genau einer Poisson-Verteilung entspricht. Kann ich trotzdem einfach so tun als sei es eine Poisson-Verteilung mit Lambda = 8? Oder muss ich ganz anders vorgehen?
Danke im Voraus und viele Grüße,
Suti
Ist das eine Poisson-Verteilung?
- Suti
- Grünschnabel

- Beiträge: 7
- Registriert: Mo 25. Mai 2020, 10:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Ist das eine Poisson-Verteilung?
Hallo Suti,
es gibt zwei Wege, Dich von der Poisson-Verteilung zu überzeugen: Entweder, wenn Du über die physikalischen Gründe des Taktens nachdenkst und das passend findest, oder wenn Du findest, dass Deine Grafik gut zu einer Poisson-Verteilung passt.
Deine Grafik sieht so aus, als könnte Sie von R produziert worden sein. Wenn das so ist, kopiere folgenden Code in Deine R-Session um 9 Beispiele für Zufallsziehungen aus einer Poissonverteilung mit lambda = 8,17 und n = 63 zu sehen. Dann wird ganz schnell klar, dass Deine Daten nicht einer Poissonverteilung entsprechen, weil sie viel zu wenig streuen.
Ich könnte mir vorstellen, dass ein verteilungsfreier Ansatz besser passt. Ich versuche mal, Deine Daten ungefähr aus der Grafik abzulesen und komme auf
Davon lassen sich 10.000 Bootstrap-Samples wie folgt ziehen:
Die Mittelwerte aus diesen 10.000 Bootstrap-Samples verteilen sich wie folgt:
Aus diesen 10.000 Bootstrap-Samples lässt sich 10.000 Mal ein 90%-Quantil bestimmen und das ist fast jedes Mal 9:
Es erscheint also verteilungsfrei angemessen, sich erst bei Werten über 9 alarmieren zu lassen.
HTH,
Bernhard
es gibt zwei Wege, Dich von der Poisson-Verteilung zu überzeugen: Entweder, wenn Du über die physikalischen Gründe des Taktens nachdenkst und das passend findest, oder wenn Du findest, dass Deine Grafik gut zu einer Poisson-Verteilung passt.
Deine Grafik sieht so aus, als könnte Sie von R produziert worden sein. Wenn das so ist, kopiere folgenden Code in Deine R-Session um 9 Beispiele für Zufallsziehungen aus einer Poissonverteilung mit lambda = 8,17 und n = 63 zu sehen. Dann wird ganz schnell klar, dass Deine Daten nicht einer Poissonverteilung entsprechen, weil sie viel zu wenig streuen.
- Code: Alles auswählen
par(mfrow=c(3,3), mar=c(2,1,1,1))
replicate(9,barplot(table(rpois(63, 8.17))))
Ich könnte mir vorstellen, dass ein verteilungsfreier Ansatz besser passt. Ich versuche mal, Deine Daten ungefähr aus der Grafik abzulesen und komme auf
- Code: Alles auswählen
beob <- c(rep(7,6), rep(8,43), rep(9, 12), 10, 11)
Davon lassen sich 10.000 Bootstrap-Samples wie folgt ziehen:
- Code: Alles auswählen
bs <- replicate(10000, sample(beob, replace = TRUE))
Die Mittelwerte aus diesen 10.000 Bootstrap-Samples verteilen sich wie folgt:
- Code: Alles auswählen
par(mfrow=c(1,1), mar = c(5, 4, 4, 2)+.1)
mittel <- apply(bs, 2, mean)
hist(mittel, breaks = 20)
Aus diesen 10.000 Bootstrap-Samples lässt sich 10.000 Mal ein 90%-Quantil bestimmen und das ist fast jedes Mal 9:
- Code: Alles auswählen
quant <- apply(bs, 2, function(x) quantile(x, .90))
table(quant)
plot(table(quant))
Es erscheint also verteilungsfrei angemessen, sich erst bei Werten über 9 alarmieren zu lassen.
HTH,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Ist das eine Poisson-Verteilung?
Hallo Bernhard,
vielen Dank für die schnelle und ausführliche Antwort! Ich glaube, ich verstehe zumindest so ungefähr deinen Ansatz.
Letzteres war auf jeden Fall der Grund meines Anfangszweifels - die Werte sehen nicht wirklich nach Poisson aus. Physikalisch sind zwar Werte auch unter 7 denkbar - aber sehr kleine Taktzahlen sind praktisch nicht möglich. Wenn das passieren würde, würde ich eher einen anderen Fehler an der Anlage vermuten. Das passt also auch nicht so richtig zu Poisson.
Genau, ich arbeite mit R und hab auch die Grafik damit erstellt. Die Beispiele sehen wirklich immer recht anders aus als meine Daten.
Die Werte hast du genau richtig abgeselen.
Zum Verständnis von "verteilungsfrei": Heißt das, dass meine Daten einfach auf keine bekannte Verteilung (Poisson oder andere) so richtig passen und man daher von einer "Spezialverteilung" ausgeht, die sich direkt aus meinen Daten ableitet?
(So einen Fall hatte ich bisher noch nicht. In den Kursen hat immer irgendeine bekannte Verteilung gepasst oder wurde vorgegeben - und damit wurde dann eben gerechnet.)
Okay, ab hier wird's etwas schwieriger und ich habe jetzt auf die Schnelle ein bisschen was über das Bootstrapping-Verfahren gelesen. Versteh ich es so richtig:
Die wahre Verteilung ist in meinem Fall nicht bekannt, Poisson und andere passen offensichtlich nicht, das heißt, meine 63-Tage-Stichprobe ist die beste Info, die ich habe.
Nun ist Bootstrapping eine Methode, bei der aus der Stichprobe eine neue Stichprobe mit Zurücklegen gezogen wird. Daraus kann ich Rückschlüsse auf die wahre Verteilung ziehen. (Sollte n hier immer gleich dem ursprünglichen n sein?)
Wenn das Ganze sehr oft wiederholt wird, folgen die Mittelwerte aus diesen ganzen Ziehungen einer Normalverteilung (wegen des zentralen Grenzwertsatzes?). Die 10.000 Mittelwerte sehen daher schon sehr glockenförmig aus.
Hab ich das soweit richtig verstanden?
Diesen letzten Schritt verstehe ich nicht ganz. Ich hätte jetzt für diese (annähernde) Normalverteilung aus dem vorherigen Schritt versucht, den Grenzwert für das 90%-Konfidenzintervall (=90%-Quartil, da einseitig) zu berechnen.
Entspricht das dem, was du gemacht hast?
Viele Grüße und danke für die viele Arbeit inklusive R-Code,
Suti
vielen Dank für die schnelle und ausführliche Antwort! Ich glaube, ich verstehe zumindest so ungefähr deinen Ansatz.
bele hat geschrieben:es gibt zwei Wege, Dich von der Poisson-Verteilung zu überzeugen: Entweder, wenn Du über die physikalischen Gründe des Taktens nachdenkst und das passend findest, oder wenn Du findest, dass Deine Grafik gut zu einer Poisson-Verteilung passt.
Letzteres war auf jeden Fall der Grund meines Anfangszweifels - die Werte sehen nicht wirklich nach Poisson aus. Physikalisch sind zwar Werte auch unter 7 denkbar - aber sehr kleine Taktzahlen sind praktisch nicht möglich. Wenn das passieren würde, würde ich eher einen anderen Fehler an der Anlage vermuten. Das passt also auch nicht so richtig zu Poisson.
bele hat geschrieben:Deine Grafik sieht so aus, als könnte Sie von R produziert worden sein. Wenn das so ist, kopiere folgenden Code in Deine R-Session um 9 Beispiele für Zufallsziehungen aus einer Poissonverteilung mit lambda = 8,17 und n = 63 zu sehen. Dann wird ganz schnell klar, dass Deine Daten nicht einer Poissonverteilung entsprechen, weil sie viel zu wenig streuen.
- Code: Alles auswählen
par(mfrow=c(3,3), mar=c(2,1,1,1))
replicate(9,barplot(table(rpois(63, 8.17))))
Genau, ich arbeite mit R und hab auch die Grafik damit erstellt. Die Beispiele sehen wirklich immer recht anders aus als meine Daten.
bele hat geschrieben:Ich könnte mir vorstellen, dass ein verteilungsfreier Ansatz besser passt. Ich versuche mal, Deine Daten ungefähr aus der Grafik abzulesen und komme auf
- Code: Alles auswählen
beob <- c(rep(7,6), rep(8,43), rep(9, 12), 10, 11)
Die Werte hast du genau richtig abgeselen.
Zum Verständnis von "verteilungsfrei": Heißt das, dass meine Daten einfach auf keine bekannte Verteilung (Poisson oder andere) so richtig passen und man daher von einer "Spezialverteilung" ausgeht, die sich direkt aus meinen Daten ableitet?
(So einen Fall hatte ich bisher noch nicht. In den Kursen hat immer irgendeine bekannte Verteilung gepasst oder wurde vorgegeben - und damit wurde dann eben gerechnet.)
bele hat geschrieben:Davon lassen sich 10.000 Bootstrap-Samples wie folgt ziehen:
- Code: Alles auswählen
bs <- replicate(10000, sample(beob, replace = TRUE))
Die Mittelwerte aus diesen 10.000 Bootstrap-Samples verteilen sich wie folgt:
- Code: Alles auswählen
par(mfrow=c(1,1), mar = c(5, 4, 4, 2)+.1)
mittel <- apply(bs, 2, mean)
hist(mittel, breaks = 20)
Okay, ab hier wird's etwas schwieriger und ich habe jetzt auf die Schnelle ein bisschen was über das Bootstrapping-Verfahren gelesen. Versteh ich es so richtig:
Die wahre Verteilung ist in meinem Fall nicht bekannt, Poisson und andere passen offensichtlich nicht, das heißt, meine 63-Tage-Stichprobe ist die beste Info, die ich habe.
Nun ist Bootstrapping eine Methode, bei der aus der Stichprobe eine neue Stichprobe mit Zurücklegen gezogen wird. Daraus kann ich Rückschlüsse auf die wahre Verteilung ziehen. (Sollte n hier immer gleich dem ursprünglichen n sein?)
Wenn das Ganze sehr oft wiederholt wird, folgen die Mittelwerte aus diesen ganzen Ziehungen einer Normalverteilung (wegen des zentralen Grenzwertsatzes?). Die 10.000 Mittelwerte sehen daher schon sehr glockenförmig aus.
Hab ich das soweit richtig verstanden?
bele hat geschrieben:Aus diesen 10.000 Bootstrap-Samples lässt sich 10.000 Mal ein 90%-Quantil bestimmen und das ist fast jedes Mal 9:
- Code: Alles auswählen
quant <- apply(bs, 2, function(x) quantile(x, .90))
table(quant)
plot(table(quant))
Es erscheint also verteilungsfrei angemessen, sich erst bei Werten über 9 alarmieren zu lassen.
Diesen letzten Schritt verstehe ich nicht ganz. Ich hätte jetzt für diese (annähernde) Normalverteilung aus dem vorherigen Schritt versucht, den Grenzwert für das 90%-Konfidenzintervall (=90%-Quartil, da einseitig) zu berechnen.
Entspricht das dem, was du gemacht hast?
Viele Grüße und danke für die viele Arbeit inklusive R-Code,
Suti
- Suti
- Grünschnabel

- Beiträge: 7
- Registriert: Mo 25. Mai 2020, 10:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Ist das eine Poisson-Verteilung?
Hallo Suti,
Das ist ganz praktisch, weil es uns eine gemeinsame Sprache gibt. Inhaltlich lässt sich das sicher auch mit vielen anderen Sprache machen.
Und damit ist die Poisson-Verteilung aus dem Spiel, weil sie viel breitere Streuung annimmt als Deine Versuchsanordnung produziert.
Wenn man eine passende Verteilung annehmen kann, dann ist das eine wertvolle Information. Wenn man die falsche Verteilung annimmt, kann die falsche Information zu falschen Ergebnissen führen. "Verteilungsfrei" heißt, dass wir für die Berechnung keine der mit Eigennamen benannten Verteilungen annehmen. Damit können wir nicht von deren Vorteilen profitieren.
Dann müssen wir jetzt klären, ob das eine Hausaufgabe für einen dieser Kurse ist oder eine Aufgabe im wirklichen Leben. Je nachdem, gehören dann Verteilungsannahme zur Aufgabenstellung, oder nicht.
Ich glaube, dass es sich für Dein Problem lohnt, sich etwas gründlicher ins Bootstrapping zu vertiefen. Wir machen dabei halt nicht die Annahme, dass Deine Beobachtungen einer namentlich benannten Verteilung folgen, dafür machen wir die Annahme, dass Deine Verteilung mit den bisher 63 Beobachtungen ausreichend gut beschrieben ist. Irgendwelche Annahmen muss man halt immer machen und Du musst Dir überlegen, ob Du zu dieser Annahme bereit bist.
Das mit dem n = n wird in praxi so gehandhabt. Ich glaube nicht, dass das so sein muss, aber ich behaupte auch nicht, da Fachmann zu sein.
Ja. Wir erhalten so eine Verteilung, wie der Mittelwert in anderen Stichproben verteilt gewesen wäre und können daraus beispielsweise 95%-Konfidenzintervalle für den Mittelwert berechnen (immer unter der Annahme, dass unsere 63 Beobachtungen die wahre Verteilung ausreichend beschreiben). Die siehst daran beispielsweise dass es recht mutig wäre, als Mittelwert für eine Poissonverteilung einfach 8,17 anzunehmen - könnte auch deutlich weniger, könnte auch deutlich mehr sein. Dein ursprünglicher Ansatz mit der Poissonverteilung berücksichtigt das nicht wirklich.
Glaube schon.
Du hättest damit ein 90%-Konfidenzintervall für den Mittelwert bestimmen können. Interessiert Dich der Mittelwert aus 63 Beobachtungrn? Du hast jetzt dank Bootstrapping 10.000 Verläufe, die die Beobachtungsreihe genausogut hätte nehmen können wie den, den sie genommen hat. Du kannst jeden Dir einfallenden Grenzwert zur Warnung/jede Dir einfallende Warnregel an diesen 10.000 prüfen, ob er/sie ausreichend oft/ausreichend selten zu einem Fehlalarm führt.
Wie lange darf denn so eine Maschine falsch laufen? Vielleicht bist Du bereit, das bis zu drei Tage lang zu akzeptieren und willst Deine Abbruchregel vom Durchschnittswert der letzten drei Tage abhängig machen? Das musst Du mit Deinem Wissen über die Anlage und die Bedeutung von Problemen mit der Taktung entscheiden. Der Bootstrapping-Ansatz bietet dazu irrsinnig viel Flexibilität.
LG,
Bernhard
Suti hat geschrieben:Genau, ich arbeite mit R ...
Das ist ganz praktisch, weil es uns eine gemeinsame Sprache gibt. Inhaltlich lässt sich das sicher auch mit vielen anderen Sprache machen.
Die Beispiele sehen wirklich immer recht anders aus als meine Daten.
Und damit ist die Poisson-Verteilung aus dem Spiel, weil sie viel breitere Streuung annimmt als Deine Versuchsanordnung produziert.
bele hat geschrieben:Zum Verständnis von "verteilungsfrei": Heißt das, dass meine Daten einfach auf keine bekannte Verteilung (Poisson oder andere) so richtig passen und man daher von einer "Spezialverteilung" ausgeht, die sich direkt aus meinen Daten ableitet?
Wenn man eine passende Verteilung annehmen kann, dann ist das eine wertvolle Information. Wenn man die falsche Verteilung annimmt, kann die falsche Information zu falschen Ergebnissen führen. "Verteilungsfrei" heißt, dass wir für die Berechnung keine der mit Eigennamen benannten Verteilungen annehmen. Damit können wir nicht von deren Vorteilen profitieren.
So einen Fall hatte ich bisher noch nicht. In den Kursen hat immer irgendeine bekannte Verteilung gepasst oder wurde vorgegeben - und damit wurde dann eben gerechnet.
Dann müssen wir jetzt klären, ob das eine Hausaufgabe für einen dieser Kurse ist oder eine Aufgabe im wirklichen Leben. Je nachdem, gehören dann Verteilungsannahme zur Aufgabenstellung, oder nicht.
Okay, ab hier wird's etwas schwieriger und ich habe jetzt auf die Schnelle ein bisschen was über das Bootstrapping-Verfahren gelesen. Versteh ich es so richtig:
Die wahre Verteilung ist in meinem Fall nicht bekannt, Poisson und andere passen offensichtlich nicht, das heißt, meine 63-Tage-Stichprobe ist die beste Info, die ich habe.
Ich glaube, dass es sich für Dein Problem lohnt, sich etwas gründlicher ins Bootstrapping zu vertiefen. Wir machen dabei halt nicht die Annahme, dass Deine Beobachtungen einer namentlich benannten Verteilung folgen, dafür machen wir die Annahme, dass Deine Verteilung mit den bisher 63 Beobachtungen ausreichend gut beschrieben ist. Irgendwelche Annahmen muss man halt immer machen und Du musst Dir überlegen, ob Du zu dieser Annahme bereit bist.
Nun ist Bootstrapping eine Methode, bei der aus der Stichprobe eine neue Stichprobe mit Zurücklegen gezogen wird. Daraus kann ich Rückschlüsse auf die wahre Verteilung ziehen. (Sollte n hier immer gleich dem ursprünglichen n sein?)
Das mit dem n = n wird in praxi so gehandhabt. Ich glaube nicht, dass das so sein muss, aber ich behaupte auch nicht, da Fachmann zu sein.
Wenn das Ganze sehr oft wiederholt wird, folgen die Mittelwerte aus diesen ganzen Ziehungen einer Normalverteilung (wegen des zentralen Grenzwertsatzes?). Die 10.000 Mittelwerte sehen daher schon sehr glockenförmig aus.
Ja. Wir erhalten so eine Verteilung, wie der Mittelwert in anderen Stichproben verteilt gewesen wäre und können daraus beispielsweise 95%-Konfidenzintervalle für den Mittelwert berechnen (immer unter der Annahme, dass unsere 63 Beobachtungen die wahre Verteilung ausreichend beschreiben). Die siehst daran beispielsweise dass es recht mutig wäre, als Mittelwert für eine Poissonverteilung einfach 8,17 anzunehmen - könnte auch deutlich weniger, könnte auch deutlich mehr sein. Dein ursprünglicher Ansatz mit der Poissonverteilung berücksichtigt das nicht wirklich.
Hab ich das soweit richtig verstanden?
Glaube schon.
Diesen letzten Schritt verstehe ich nicht ganz. Ich hätte jetzt für diese (annähernde) Normalverteilung aus dem vorherigen Schritt versucht, den Grenzwert für das 90%-Konfidenzintervall (=90%-Quartil, da einseitig) zu berechnen.
Entspricht das dem, was du gemacht hast?
Du hättest damit ein 90%-Konfidenzintervall für den Mittelwert bestimmen können. Interessiert Dich der Mittelwert aus 63 Beobachtungrn? Du hast jetzt dank Bootstrapping 10.000 Verläufe, die die Beobachtungsreihe genausogut hätte nehmen können wie den, den sie genommen hat. Du kannst jeden Dir einfallenden Grenzwert zur Warnung/jede Dir einfallende Warnregel an diesen 10.000 prüfen, ob er/sie ausreichend oft/ausreichend selten zu einem Fehlalarm führt.
Wie lange darf denn so eine Maschine falsch laufen? Vielleicht bist Du bereit, das bis zu drei Tage lang zu akzeptieren und willst Deine Abbruchregel vom Durchschnittswert der letzten drei Tage abhängig machen? Das musst Du mit Deinem Wissen über die Anlage und die Bedeutung von Problemen mit der Taktung entscheiden. Der Bootstrapping-Ansatz bietet dazu irrsinnig viel Flexibilität.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Ist das eine Poisson-Verteilung?
Hallo Bernhard,
ich habe jetzt ein bisschen für die Antwort gebraucht, weil ich erstmal über deine Erklärungen nachdenken musste und auch über's Bootstrapping noch ein paar Sachen angeschaut habe. Das ist wirklich eine interessante Methode, mit der man offensichtig so einiges machen kann.
Okay, verstehe. Da war ich wohl gedanklich drüber gestolpert, weil in den Kursen die Beispiele immer so konstruiert waren, dass eine bestimmte Verteilung gepasst hat oder sie wurde halt vorgegeben. (Z. B. hieß es dann für eine Poisson-Verteilung: "Am Tag rufen im Durchschnitt 12 Personen bei der Hotline an." und dann konnte man losrechnen.)
Nein, mit den Kursen bin ich durch. Jetzt versuche ich, das Gelernte auf reale Beispiele aus meiner Praxis anzuwenden. Und natürlich auch noch Neues dazuzulernen
Darüber habe ich mir jetzt einige Gedanken gemacht und bin im Kopf auch nochmal einen Schritt zurückgegangen zur Poisson-Verteilung. Ich hab mir überlegt, wie eine sinnvolle Abbruchregel aussehen könnte (bzw. in meinem Fall wäre es eine Warnregel) und wie ich das im Falle einer Poisson-Verteilung rechnen würde.
Dann hab ich versucht, das Ganze auf den verteilungsfreien Ansatz zu übertragen, bin aber noch nicht wirklich sicher, ob meine Ideen in die richtige Richtung gehen.
Hier mal mein Gedankengang:
----------------------------------------------------------------------------------
TEIL 1: Poisson-Verteilung
Nehmen wir an, ich wäre recht sicher, dass die Taktungen meiner Anlage einer Poisson-Verteilung folgen. Der Mittelwert der Taktungen pro Tag liegt bei 8. Das weiß ich, weil es in der Betriebsanleitung steht (hab ich mir jetzt ausgedacht...).
Meine Verteilung würde dann so aussehen:
Das 90%-Quantil wäre hier z. B. 12, das 99%-Quantil wäre 15:
Damit könnte ich mir eine Regel erstellen für einen Grenzwert, ab dem ich gewarnt werden will.
Allerdings überlege ich mir jetzt, dass ich die Überprüfung eines einzelnen Tageswertes nicht so sinnvoll finde. Denn ein Fehler im Bauteil wäre für die Anlage jetzt erstmal nicht so kritisch, sie würde dadurch nur ineffizienter laufen. Ich würde nicht sofort bei einem einzelnen hohen Wert losspringen wollen, um das Bauteil auszutauschen, denn da könnte auch mal irgendwas anderes dahinterstecken.
Es wäre nur gut mitzubekommen, wenn sich allgemein der Trend der Taktzahlen pro Tag nach oben entwickeln würde, denn das würde für einen langsamen Verschleiß des Bauteils sprechen.
Ich überlege mir also eine andere Regel, z. B. erst eine Warnung zu erhalten, wenn mehrere aufeinanderfolgende Werte über einem bestimmten Grenzwert liegen.
Oder ich könnte die Mittelwerte über mehrere Betriebstage anschauen (rollierend) und überprüfen, ob der "wahre" Mittelwert wahrscheinlich noch bei 8 liegt.
Dabei hilft mir der zentrale Grenzwertsatz, weil die Mittelwerte aus mehreren Stichproben einer Normalverteilung folgen. Um eine robuste Schätzung mit ausreichend Stichproben zu ermöglichen, schaue ich mir jeweils die letzten 30 Betriebstage an.
Meine Normalverteilung der Stichprobenmittelwerte hätte also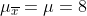 und
und 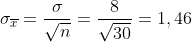 .
.
Das 90%- bzw. 99%-Quantil für die Mittelwerte aus 30 Betriebstagen liegen dann bei 9,9 bzw. 11,4:
Ich könnte mir also entsprechend eine Warnung ausgeben lassen, wenn der rollierende Mittelwert den Grenzwert zum gewählten Konfidenzniveau übersteigt.
----------------------------------------------------------------------------------
TEIL 2: Verteilungsfreier Ansatz
Wenn ich davon ausgehe, dass die Poission-Verteilung nicht auf mein Szenario passt, wie oben diskutiert, hilft mir die Bootstrapping-Methode, um trotzdem aus einer Stichprobe aus der fehlerfreien Betriebszeit Annahmen über die wahre Verteilung zu treffen.
Ich simuliere aus meiner Stichprobe 10.000 weitere mögliche Stichproben, wie oben von dir gezeigt:
Daraus kann ich jeweils den Mittelwert berechnen und bekomme so einen guten Eindruck über die mögliche Verteilung der Stichprobenmittelwerte:
Hier bin ich jetzt darüber gestolpert, dass diese Mittelwerte nicht sehr normalverteilt aussehen, obwohl n mit 63 doch recht groß ist:
Ich vermute, dass liegt daran, dass wir hier nicht wie beim zentralen Grenzwertsatz vorgegangen sind (viele Stichproben ohne Zurücklegen aus einer bekannten Grundgesamtheit ziehen), sondern unsere Stichproben ja mit Zurücklegen aus der Ausgangsstichprobe gezogen wurden. Ist also was anderes.
Jetzt bin ich allerdings unsicher, wie ich in diesem Fall meine Hypothesen "Aktueller Mittelwert der Taktzahlen hat sich nicht verändert" vs. "Aktueller Mittelwert der Taktzahlen ist inzwischen höher geworden" überprüfen kann.
Muss ich meinen aktuell gemessenen Mittelwert (z. B. wieder über die letzten 30 Tage) zu gewünschtem Konfidenzniveau nun einfach mit dem Grenzwert aus der oben berechneten Verteilung der Mittelwerte vergleichen? Bei α = 0,01 müsste der Grenzwert dann ja 8,29 sein bzw. bei α = 0,001 wäre er 8,38.
Oder muss ich über den zentralen Grenzwertsatz versuchen, wieder zu einer Normalverteilung zu kommen? Dazu bräuchte ich dann wieder μ und σ.
μ = 8,175 und σ = 0,685?
Oder μ = 8,174 und σ = 0,671?
Oder bin ich da ganz auf dem Holzweg?
Hier fehlt mir doch noch etwas das Verständnis, wie ich mit meinen "gebootstrappten" Daten weiterarbeiten kann, ohne totalen Unsinn zu rechnen.
Vom konkreten Fall her fände ich die Überprüfung des Mittelwerts über einen bestimmten Zeitraum auf jeden Fall am sinnvollsten, sinnvoller als einen Grenzwert für einen einzelnen Messwert.
Vielleicht kannst du mir noch einen Tipp geben, in welche Richtung ich da weitergehen sollte?
Vielen Dank im Voraus, allein schon für's Lesen,
Suti
ich habe jetzt ein bisschen für die Antwort gebraucht, weil ich erstmal über deine Erklärungen nachdenken musste und auch über's Bootstrapping noch ein paar Sachen angeschaut habe. Das ist wirklich eine interessante Methode, mit der man offensichtig so einiges machen kann.
Wenn man eine passende Verteilung annehmen kann, dann ist das eine wertvolle Information. Wenn man die falsche Verteilung annimmt, kann die falsche Information zu falschen Ergebnissen führen. "Verteilungsfrei" heißt, dass wir für die Berechnung keine der mit Eigennamen benannten Verteilungen annehmen. Damit können wir nicht von deren Vorteilen profitieren.
Okay, verstehe. Da war ich wohl gedanklich drüber gestolpert, weil in den Kursen die Beispiele immer so konstruiert waren, dass eine bestimmte Verteilung gepasst hat oder sie wurde halt vorgegeben. (Z. B. hieß es dann für eine Poisson-Verteilung: "Am Tag rufen im Durchschnitt 12 Personen bei der Hotline an." und dann konnte man losrechnen.)
Dann müssen wir jetzt klären, ob das eine Hausaufgabe für einen dieser Kurse ist oder eine Aufgabe im wirklichen Leben. Je nachdem, gehören dann Verteilungsannahme zur Aufgabenstellung, oder nicht.
Nein, mit den Kursen bin ich durch. Jetzt versuche ich, das Gelernte auf reale Beispiele aus meiner Praxis anzuwenden. Und natürlich auch noch Neues dazuzulernen
Wie lange darf denn so eine Maschine falsch laufen? Vielleicht bist Du bereit, das bis zu drei Tage lang zu akzeptieren und willst Deine Abbruchregel vom Durchschnittswert der letzten drei Tage abhängig machen? Das musst Du mit Deinem Wissen über die Anlage und die Bedeutung von Problemen mit der Taktung entscheiden. Der Bootstrapping-Ansatz bietet dazu irrsinnig viel Flexibilität.
Darüber habe ich mir jetzt einige Gedanken gemacht und bin im Kopf auch nochmal einen Schritt zurückgegangen zur Poisson-Verteilung. Ich hab mir überlegt, wie eine sinnvolle Abbruchregel aussehen könnte (bzw. in meinem Fall wäre es eine Warnregel) und wie ich das im Falle einer Poisson-Verteilung rechnen würde.
Dann hab ich versucht, das Ganze auf den verteilungsfreien Ansatz zu übertragen, bin aber noch nicht wirklich sicher, ob meine Ideen in die richtige Richtung gehen.
Hier mal mein Gedankengang:
----------------------------------------------------------------------------------
TEIL 1: Poisson-Verteilung
Nehmen wir an, ich wäre recht sicher, dass die Taktungen meiner Anlage einer Poisson-Verteilung folgen. Der Mittelwert der Taktungen pro Tag liegt bei 8. Das weiß ich, weil es in der Betriebsanleitung steht (hab ich mir jetzt ausgedacht...).
Meine Verteilung würde dann so aussehen:
- Code: Alles auswählen
x <- 0:20
barplot(dpois(x, lambda = 8), names.arg = x)
Das 90%-Quantil wäre hier z. B. 12, das 99%-Quantil wäre 15:
- Code: Alles auswählen
qpois(0.9, lambda = 8)
qpois(0.99, lambda = 8)
Damit könnte ich mir eine Regel erstellen für einen Grenzwert, ab dem ich gewarnt werden will.
Allerdings überlege ich mir jetzt, dass ich die Überprüfung eines einzelnen Tageswertes nicht so sinnvoll finde. Denn ein Fehler im Bauteil wäre für die Anlage jetzt erstmal nicht so kritisch, sie würde dadurch nur ineffizienter laufen. Ich würde nicht sofort bei einem einzelnen hohen Wert losspringen wollen, um das Bauteil auszutauschen, denn da könnte auch mal irgendwas anderes dahinterstecken.
Es wäre nur gut mitzubekommen, wenn sich allgemein der Trend der Taktzahlen pro Tag nach oben entwickeln würde, denn das würde für einen langsamen Verschleiß des Bauteils sprechen.
Ich überlege mir also eine andere Regel, z. B. erst eine Warnung zu erhalten, wenn mehrere aufeinanderfolgende Werte über einem bestimmten Grenzwert liegen.
Oder ich könnte die Mittelwerte über mehrere Betriebstage anschauen (rollierend) und überprüfen, ob der "wahre" Mittelwert wahrscheinlich noch bei 8 liegt.
Dabei hilft mir der zentrale Grenzwertsatz, weil die Mittelwerte aus mehreren Stichproben einer Normalverteilung folgen. Um eine robuste Schätzung mit ausreichend Stichproben zu ermöglichen, schaue ich mir jeweils die letzten 30 Betriebstage an.
Meine Normalverteilung der Stichprobenmittelwerte hätte also
- Code: Alles auswählen
y <- seq(3,13, by = 0.1)
plot(y, dnorm(y, mean = 8, sd = 1.46), type = "l")
Das 90%- bzw. 99%-Quantil für die Mittelwerte aus 30 Betriebstagen liegen dann bei 9,9 bzw. 11,4:
- Code: Alles auswählen
qnorm(0.95, mean = 8, sd = 1.46)
qnorm(0.99, mean = 8, sd = 1.46)
Ich könnte mir also entsprechend eine Warnung ausgeben lassen, wenn der rollierende Mittelwert den Grenzwert zum gewählten Konfidenzniveau übersteigt.
----------------------------------------------------------------------------------
TEIL 2: Verteilungsfreier Ansatz
Wenn ich davon ausgehe, dass die Poission-Verteilung nicht auf mein Szenario passt, wie oben diskutiert, hilft mir die Bootstrapping-Methode, um trotzdem aus einer Stichprobe aus der fehlerfreien Betriebszeit Annahmen über die wahre Verteilung zu treffen.
Ich simuliere aus meiner Stichprobe 10.000 weitere mögliche Stichproben, wie oben von dir gezeigt:
- Code: Alles auswählen
beob <- c(rep(7,6), rep(8,43), rep(9, 12), 10, 11)
bs <- replicate(10000, sample(beob, replace = TRUE))
Daraus kann ich jeweils den Mittelwert berechnen und bekomme so einen guten Eindruck über die mögliche Verteilung der Stichprobenmittelwerte:
- Code: Alles auswählen
mittel <- apply(bs, 2, mean)
Hier bin ich jetzt darüber gestolpert, dass diese Mittelwerte nicht sehr normalverteilt aussehen, obwohl n mit 63 doch recht groß ist:
- Code: Alles auswählen
hist(mittel, breaks = 30)
Ich vermute, dass liegt daran, dass wir hier nicht wie beim zentralen Grenzwertsatz vorgegangen sind (viele Stichproben ohne Zurücklegen aus einer bekannten Grundgesamtheit ziehen), sondern unsere Stichproben ja mit Zurücklegen aus der Ausgangsstichprobe gezogen wurden. Ist also was anderes.
Jetzt bin ich allerdings unsicher, wie ich in diesem Fall meine Hypothesen "Aktueller Mittelwert der Taktzahlen hat sich nicht verändert" vs. "Aktueller Mittelwert der Taktzahlen ist inzwischen höher geworden" überprüfen kann.
Muss ich meinen aktuell gemessenen Mittelwert (z. B. wieder über die letzten 30 Tage) zu gewünschtem Konfidenzniveau nun einfach mit dem Grenzwert aus der oben berechneten Verteilung der Mittelwerte vergleichen? Bei α = 0,01 müsste der Grenzwert dann ja 8,29 sein bzw. bei α = 0,001 wäre er 8,38.
- Code: Alles auswählen
quantile(mittel, probs = 0.9)
quantile(mittel, probs = 0.99)
Oder muss ich über den zentralen Grenzwertsatz versuchen, wieder zu einer Normalverteilung zu kommen? Dazu bräuchte ich dann wieder μ und σ.
μ = 8,175 und σ = 0,685?
- Code: Alles auswählen
mean(beob)
sd(beob)
Oder μ = 8,174 und σ = 0,671?
- Code: Alles auswählen
mean(mittel)
stabweichung <- apply(bs, 2, sd)
mean(stabweichung)
Oder bin ich da ganz auf dem Holzweg?
Hier fehlt mir doch noch etwas das Verständnis, wie ich mit meinen "gebootstrappten" Daten weiterarbeiten kann, ohne totalen Unsinn zu rechnen.
Vom konkreten Fall her fände ich die Überprüfung des Mittelwerts über einen bestimmten Zeitraum auf jeden Fall am sinnvollsten, sinnvoller als einen Grenzwert für einen einzelnen Messwert.
Vielleicht kannst du mir noch einen Tipp geben, in welche Richtung ich da weitergehen sollte?
Vielen Dank im Voraus, allein schon für's Lesen,
Suti
- Suti
- Grünschnabel

- Beiträge: 7
- Registriert: Mo 25. Mai 2020, 10:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Ist das eine Poisson-Verteilung?
Hallo Suti,
Das klingt sehr vernünftig.
Naja, die Beurteilung des Histogramms ist halt auch subjektiv. Ich finde das schon ganz schön nah an der Normalverteilung dran, wenn man im Kopf hat, dass Deine Ausgangsdaten im Wesentlichen aus der Zahl 8 mit einigen eingestreuten 9 bestehen. Wenn Du es gerne etwas "normaler" hättest, dann kannst Du die Zahl der Bootstrapping-Samples heraufsetzen. Wenn Du statt der zehntausend beispielsweise 1 Million nimmst, dann rechnet dann Rechner zwar spürbar länger, bleibt aber im Messbereich "Sekunden". Dann wird das Histogramm auch glatter. Mit 10 Millionen wird es noch glatter werden. Du kannst halt nur endlich viele Samples ziehen und über endlich viele sagt der Grenzwertsatz nichts konkretes.
Als Ingenieur haben wir Chancen, dass Du ein wenig C oder C++ kannst. Schon möglich, dass ein geschickter Programmierer in einer compilierten Programmiersprache diese Bootstrapping-Geschichten sehr viel performanter lösen kann, als ich das hier in R vorschlage. Es bringt aber auch nichts, das Bootstrapping auf die x-tew Nachkommastelle zu betreiben, wenn wir aus 63 gerundeten Beobachtungen Schlussfolgerungen ziehen wollen.
Nehmen wir mal an, Du kannst drei Tage lang zuschauen weil Du weißt, dass in diesen drei Tagen nichts explodiert. Du addierst also über drei Tage hinweg die Taktungen Deiner Anlage. Wir ziehen jetzt hunderttausend Mal eine Bootstrap-Stichprobe, die drei Tage repräsentiert und berechnen die Taktungssumme in diesen drei Tagen:
Das streut doch schon sehr viel breiter als die Beobachtungen an einem Tag. Jetzt stellt sich die Frage, wo Du den Cutoff für die Warnung legen willst, damit Du nicht zu oft gewarnt wirst. Dabei hilft die empirische cummulative Verteilungsfunktion:
Ich habe eine rote Linie bei 90% Häufigkeit eingezogen. Daher siehst Du leicht, dass bei normaler Funktion die Summe aus drei Tagen in mindestens 90% der Beobachtungen weniger als 26 beträgt (Plausibilitätscheck: Der häufigste Wert ist 8, 3x8=24 liegt unter 26). In mindestens 95% der 3-Tages-Intervalle liegt die Anzahl der Taktungen bei weniger als 27. Du solltest die Simulation ein paar mal wiederholen, um Dich zu überzeugen, dass 26 bzw 27 als Grenzwert wiederholungsstabil ist.
LG,
Bernhard
Suti hat geschrieben:ich habe jetzt ein bisschen für die Antwort gebraucht, weil ich erstmal über deine Erklärungen nachdenken musste und auch über's Bootstrapping noch ein paar Sachen angeschaut habe.
Das klingt sehr vernünftig.
- Code: Alles auswählen
mittel <- apply(bs, 2, mean)
Hier bin ich jetzt darüber gestolpert, dass diese Mittelwerte nicht sehr normalverteilt aussehen, obwohl n mit 63 doch recht groß ist:
- Code: Alles auswählen
hist(mittel, breaks = 30)
Ich vermute, dass liegt daran, dass wir hier nicht wie beim zentralen Grenzwertsatz vorgegangen sind (viele Stichproben ohne Zurücklegen aus einer bekannten Grundgesamtheit ziehen), sondern unsere Stichproben ja mit Zurücklegen aus der Ausgangsstichprobe gezogen wurden.
Naja, die Beurteilung des Histogramms ist halt auch subjektiv. Ich finde das schon ganz schön nah an der Normalverteilung dran, wenn man im Kopf hat, dass Deine Ausgangsdaten im Wesentlichen aus der Zahl 8 mit einigen eingestreuten 9 bestehen. Wenn Du es gerne etwas "normaler" hättest, dann kannst Du die Zahl der Bootstrapping-Samples heraufsetzen. Wenn Du statt der zehntausend beispielsweise 1 Million nimmst, dann rechnet dann Rechner zwar spürbar länger, bleibt aber im Messbereich "Sekunden". Dann wird das Histogramm auch glatter. Mit 10 Millionen wird es noch glatter werden. Du kannst halt nur endlich viele Samples ziehen und über endlich viele sagt der Grenzwertsatz nichts konkretes.
Als Ingenieur haben wir Chancen, dass Du ein wenig C oder C++ kannst. Schon möglich, dass ein geschickter Programmierer in einer compilierten Programmiersprache diese Bootstrapping-Geschichten sehr viel performanter lösen kann, als ich das hier in R vorschlage. Es bringt aber auch nichts, das Bootstrapping auf die x-tew Nachkommastelle zu betreiben, wenn wir aus 63 gerundeten Beobachtungen Schlussfolgerungen ziehen wollen.
Jetzt bin ich allerdings unsicher, wie ich in diesem Fall meine Hypothesen "Aktueller Mittelwert der Taktzahlen hat sich nicht verändert" vs. "Aktueller Mittelwert der Taktzahlen ist inzwischen höher geworden" überprüfen kann.
[...]
Hier fehlt mir doch noch etwas das Verständnis, wie ich mit meinen "gebootstrappten" Daten weiterarbeiten kann, ohne totalen Unsinn zu rechnen.
Nehmen wir mal an, Du kannst drei Tage lang zuschauen weil Du weißt, dass in diesen drei Tagen nichts explodiert. Du addierst also über drei Tage hinweg die Taktungen Deiner Anlage. Wir ziehen jetzt hunderttausend Mal eine Bootstrap-Stichprobe, die drei Tage repräsentiert und berechnen die Taktungssumme in diesen drei Tagen:
- Code: Alles auswählen
beob <- c(rep(7,6), rep(8,43), rep(9, 12), 10, 11)
summe.aus.drei <- function() sum(sample(x = beob, size = 3, replace = TRUE))
n <- 100000
samples <- replicate(n, summe.aus.drei())
plot(table(samples), xlab="Summe aus drei Tagen", ylab="Häufigkeit")
print(table(samples))
Das streut doch schon sehr viel breiter als die Beobachtungen an einem Tag. Jetzt stellt sich die Frage, wo Du den Cutoff für die Warnung legen willst, damit Du nicht zu oft gewarnt wirst. Dabei hilft die empirische cummulative Verteilungsfunktion:
- Code: Alles auswählen
plot(ecdf(samples))
abline(h=.9, col = "red")
Ich habe eine rote Linie bei 90% Häufigkeit eingezogen. Daher siehst Du leicht, dass bei normaler Funktion die Summe aus drei Tagen in mindestens 90% der Beobachtungen weniger als 26 beträgt (Plausibilitätscheck: Der häufigste Wert ist 8, 3x8=24 liegt unter 26). In mindestens 95% der 3-Tages-Intervalle liegt die Anzahl der Taktungen bei weniger als 27. Du solltest die Simulation ein paar mal wiederholen, um Dich zu überzeugen, dass 26 bzw 27 als Grenzwert wiederholungsstabil ist.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Ist das eine Poisson-Verteilung?
Hallo Bernhard,
mit der Summe aus mehreren Tagen zu rechnen, klingt plausibel. Ich gehe allerdings davon aus, dass ein Verschleiß des Bauteils sehr langsam und schleichend vonstatten gehen würde, so dass ich wohl größere Zeiträume anschauen muss (also mehr als drei Tage).
Wäre mein Versuch von oben, einen Mittelwertvergleich zwischen aktuellen Daten und den Ausgangsdaten zu machen, auch mathematisch richtig, oder kann ich das so nicht machen in Kombination mit dem Bootstrapping?
Irgendwie hab ich immer so das Szenario im Kopf, dass für meine aktuellen Messwerte die Hypothese überprüft werden muss, dass der Mittelwert noch da liegt, wo er vorher war. Falls er signifikant (nach oben) abweicht, wäre das ein Indiz für eine Verschleißerscheinung am nachgerüsteten Bauteil.
Oder denke ich da zu sehr nach "Kursschema", so wie es meistens in den Beispielaufgaben gemacht wurde?
Viele Grüße,
Suti
mit der Summe aus mehreren Tagen zu rechnen, klingt plausibel. Ich gehe allerdings davon aus, dass ein Verschleiß des Bauteils sehr langsam und schleichend vonstatten gehen würde, so dass ich wohl größere Zeiträume anschauen muss (also mehr als drei Tage).
Wäre mein Versuch von oben, einen Mittelwertvergleich zwischen aktuellen Daten und den Ausgangsdaten zu machen, auch mathematisch richtig, oder kann ich das so nicht machen in Kombination mit dem Bootstrapping?
Irgendwie hab ich immer so das Szenario im Kopf, dass für meine aktuellen Messwerte die Hypothese überprüft werden muss, dass der Mittelwert noch da liegt, wo er vorher war. Falls er signifikant (nach oben) abweicht, wäre das ein Indiz für eine Verschleißerscheinung am nachgerüsteten Bauteil.
Oder denke ich da zu sehr nach "Kursschema", so wie es meistens in den Beispielaufgaben gemacht wurde?
Viele Grüße,
Suti
- Suti
- Grünschnabel

- Beiträge: 7
- Registriert: Mo 25. Mai 2020, 10:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Ist das eine Poisson-Verteilung?
Mittelwerte aus n Tagen und Summenwerte aus n Tagen sind erstmal gleichwertig. Sie unterscheiden sich durch einen konstanten Faktor. Das ist wurscht.
Du darfst auch gerne die gebootstrapte Verteilung als normal ansehen und mit deren Mittelwert und Standardabweichung rechnen.
Aber die Mittelwerte aus 63 Tagen streuen weniger als die Mittelwerte aus 30 Tagen. Je mehr Daten Du hast, umso genauer ist der wahre Mittelwert bestimmt. Deshalb würde ich 30-Tage-Beobachtungen auch mit 30-Tage Bootstrapsamples vergleichen.
LG,
Bernhard
Du darfst auch gerne die gebootstrapte Verteilung als normal ansehen und mit deren Mittelwert und Standardabweichung rechnen.
Aber die Mittelwerte aus 63 Tagen streuen weniger als die Mittelwerte aus 30 Tagen. Je mehr Daten Du hast, umso genauer ist der wahre Mittelwert bestimmt. Deshalb würde ich 30-Tage-Beobachtungen auch mit 30-Tage Bootstrapsamples vergleichen.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Ist das eine Poisson-Verteilung?
Hallo Bernhard,
(ich hoffe, ich nerve noch nicht. Ich versuche gerade alles, was geht, durchzugehen und Varianten auszuprobieren und du bist da echt eine riesen Hilfe!)
Ich versuche gerade alles, was geht, durchzugehen und Varianten auszuprobieren und du bist da echt eine riesen Hilfe!)
Du hast Recht, das sollte eigentlich auf's selbe rauskommen. Manchmal hab ich echt noch einen Knoten im Hirn...
Okay, das hätte ich dann erstmal so versucht:
Wenn ich dann vergleiche mit (Beispiel-)Taktzahlen aus den letzten 30 Tagen:
--> Signifikanter Unterschied, Warnung würde ausgegeben
Allerdings muss ich noch das hier beachten:
Stimmt, das war ja auch beim T-Test so, dass man (ungefähr) gleiche Varianzen gebraucht hat, wenn ich mich recht erinnere.
Das heißt aber, ich müsste dann das hier machen?
Oder müsste ich meine Ausgangsdaten (Normalbetrieb) auf 30 Tage "kürzen"? Beim ersten Fall wäre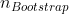 nicht mehr gleich
nicht mehr gleich 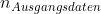 , beim zweiten Fall würde ich einige Informationen über meine wahre Verteilung verlieren?
, beim zweiten Fall würde ich einige Informationen über meine wahre Verteilung verlieren?
Viele Grüße,
im Rechenfieber
Suti
(ich hoffe, ich nerve noch nicht.
Mittelwerte aus n Tagen und Summenwerte aus n Tagen sind erstmal gleichwertig. Sie unterscheiden sich durch einen konstanten Faktor. Das ist wurscht.
Du hast Recht, das sollte eigentlich auf's selbe rauskommen. Manchmal hab ich echt noch einen Knoten im Hirn...
Du darfst auch gerne die gebootstrapte Verteilung als normal ansehen und mit deren Mittelwert und Standardabweichung rechnen.
Okay, das hätte ich dann erstmal so versucht:
- Code: Alles auswählen
beob <- c(rep(7,6), rep(8,43), rep(9, 12), 10, 11)
bs <- replicate(10000, sample(beob, replace = TRUE))
mittel <- apply(bs, 2, mean)
grenzwert <- qnorm(0.95, mean = mean(mittel), sd = sd(mittel))
[1] 8.316531
Wenn ich dann vergleiche mit (Beispiel-)Taktzahlen aus den letzten 30 Tagen:
- Code: Alles auswählen
beob_neu <- c(rep(7,2), rep(8,16), rep(9, 8), rep(10,2), rep(11,2))
mean(beob_neu)
[1] 8.533333
--> Signifikanter Unterschied, Warnung würde ausgegeben
Allerdings muss ich noch das hier beachten:
Aber die Mittelwerte aus 63 Tagen streuen weniger als die Mittelwerte aus 30 Tagen. Je mehr Daten Du hast, umso genauer ist der wahre Mittelwert bestimmt. Deshalb würde ich 30-Tage-Beobachtungen auch mit 30-Tage Bootstrapsamples vergleichen.
Stimmt, das war ja auch beim T-Test so, dass man (ungefähr) gleiche Varianzen gebraucht hat, wenn ich mich recht erinnere.
Das heißt aber, ich müsste dann das hier machen?
- Code: Alles auswählen
bs_30 <- replicate(10000, sample(beob, size = 30, replace = TRUE))
Oder müsste ich meine Ausgangsdaten (Normalbetrieb) auf 30 Tage "kürzen"? Beim ersten Fall wäre
Viele Grüße,
im Rechenfieber
Suti
- Suti
- Grünschnabel

- Beiträge: 7
- Registriert: Mo 25. Mai 2020, 10:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Ist das eine Poisson-Verteilung?
Suti hat geschrieben:Okay, das hätte ich dann erstmal so versucht:
- Code: Alles auswählen
beob <- c(rep(7,6), rep(8,43), rep(9, 12), 10, 11)
bs <- replicate(10000, sample(beob, replace = TRUE))
mittel <- apply(bs, 2, mean)
grenzwert <- qnorm(0.95, mean = mean(mittel), sd = sd(mittel))
[1] 8.316531
Solange Du dabei nicht vergisst, dass Deine Datenbasis nicht wirklich eine Angabe bis auf die 6. Nachkommastelle rechtfertigt...
Das heißt aber, ich müsste dann das hier machen?
- Code: Alles auswählen
bs_30 <- replicate(10000, sample(beob, size = 30, replace = TRUE))
Das wäre mein Vorschlag.
Oder müsste ich meine Ausgangsdaten (Normalbetrieb) auf 30 Tage "kürzen"? Beim ersten Fall wärenicht mehr gleich
, beim zweiten Fall würde ich einige Informationen über meine wahre Verteilung verlieren?
Informationen über die wahre Verteilung zu verschenken kannst Du Dir nicht leisten, deshalb liegt die richtige Antwort IMHO auf der Hand.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Wer ist online?
Mitglieder in diesem Forum: Google [Bot] und 6 Gäste


