STATISTIK-FORUM.de

[kilianlaurenz]

Hallo an alle,

ich habe eine Frage zu der Entscheidungstabelle bei Hypothesentests. Am Ende des Beitrages verdeutliche ich mein Problem an einem Beispiel. Ich verwende die nachfolgende Notation:


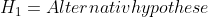
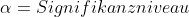
(üblicherweise und auch in diesem Beitrag 5%)


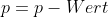
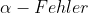
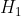
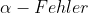
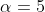
Wenn ich das richtig verstehe ist es so, dass mein p-Wert angibt, mit welcher Wahrscheinlichkeit ich einen Fehler 1. Art () begehe, also annehmen, obwohl wahr ist. Je geringer der p-Wert, desto geringer die Wahrscheinlichkeit einen zu begehen. Unterschreitet mein p-Wert eine vorher festgelegte Grenze (Signifikanzniveau %), ist das Risiko klein genug, so dass ich mich für entscheide. 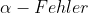Gleichzeitig - und das ist mein eigentliches Verständnisproblem - beträgt aber die Wahrscheinlichkeit, keinen (!) zu begehen, . 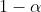Das bedeutet anzunehmen, wenn richtig ist. 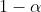Also je kleiner , desto größer (logisch). 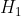Warum entscheide ich mich aber (bei p<) für und nicht für ?

Beispiel:





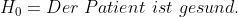
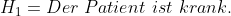
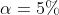
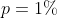
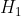
Der Hypothesentest ist signifikant, daher wird verworfen und angenommen. Das leuchtet ein, da die Wahrscheinlichkeit, den Patienten als krank zu diagnostizieren, obwohl er gesund ist, mit 1% sehr gering ist. Für mich wäre es aber auch genauso einleuchtend, anzunehmen, da die Wahrscheinlichkeit, den Patienten als gesund zu diagnostizieren, wenn er tatsächlich gesund ist, mit 99% sehr hoch ist.

Ich kann leider nicht erkennen, wo mein Denkfehler liegt.


Ich freue mich, über hilfreiche Anmerkungen. Vielen Dank schonmal.


Kilian-Laurenz Hof

[PonderStibbons]

Wenn ich das richtig verstehe ist es so, dass mein p-Wert angibt, mit welcher Wahrscheinlichkeit ich einen Fehler 1. Art () begehe, also annehmen, obwohl wahr ist.

Nicht obwohl, sondern falls. Ist H0 falsch, ist die Möglichkeit für einen Fehler 1. Art gleich Null.

Je geringer der p-Wert, desto geringer die Wahrscheinlichkeit einen zu begehen.

Nein. Je geringer der p-Wert, desto unwahrscheinlicher sind die gefundenen Stichproben-Daten,
wenn man annimmt, dass H0 gilt. Der p-Wet sagt nichts über die Wahrscheinlichkeit der Nullhypothese
aus. Er bedeutet p(Daten|H0), nicht p(H0|Daten).

Unterschreitet mein p-Wert eine vorher festgelegte Grenze (Signifikanzniveau %), ist das Risiko klein genug, so dass ich mich für entscheide. Gleichzeitig - und das ist mein eigentliches Verständnisproblem - beträgt aber die Wahrscheinlichkeit, keinen (!) zu begehen, .

Nein,wie gesagt geht es nicht um p(H0) oder p(nicht-H0), sondern um p(Daten|H0).

Mit freundlichen Grüßen

PonderStibbons

[kilianlaurenz]

Hallo,

vielen Dank für die hilfreiche Nachhilfestunde in Aussagenlogik. Also mein Fehler war, dass ich mit

Wahrscheinlichkeit, dass H0 richtig ist, falls ich mich für H1 entscheide [p(H0|Daten)]

übersetzt habe und nicht richtigerweise mit

Wahrscheinlichkeit, dass meine Stichproben-Daten in der Grundgesamtheit gefunden werden, falls H0 richtig ist. [p(Daten|H0)]


Aber wie kann die Wahrscheinlichkeit sinnvoll interpretiert werden? Das wäre doch dann die Wahrscheinlichkeit für nicht-p(Daten|H0), also die

Wahrscheinlichkeit, dass nicht meine Stichproben-Daten in der Grundgesamtheit gefunden werden, falls H0 richtig ist. [nicht-p(Daten|H0)]




Vielen Dank für die Hilfe. Mit freundlichem Gruß.


Kilian-Laurenz Hof

[PonderStibbons]

Aber wie kann die Wahrscheinlichkeit sinnvoll interpretiert werden?

Gar nicht.

Mit freundlichen Grüßen

PonderStibbons