STATISTIK-FORUM.de

[stumper77]

Hallo Leute,
ich muss zur Zeit Messdaten auswerten und brauche da mal ein wenig Hilfe der Statistikfreunde.
Meine Messdaten sind 20 Werte, die zwischen 0,000 – 0,004 liegen müssen.
Meine Ergebnisse sind nicht normalverteilt. Dies erkennt man schon an den erstellten Boxplots. Jetzt muss ich das rechnerisch noch darstellen. Doch wie mach ich das?

Noch ein paar Infos: ich habe verschiedene Einstellungen eine Maschine probiert und muss nun die stabilste oder reproduzierbarste Einstellung herausfinden. Die grafische Darstellung bekomme ich ganz gut hin nur die rechnerische nicht.

Hat jemand da einen Tipp für mich?

Viele Grüße

[bele]

Was verstehst Du unter der rechnerischen Darstellung? Du hast 20 Werte eingestellt und 20 Werte herausbekommen? Oder hast Du 2 verschiedene Werte je 10x gemessen? Am besten stellst Du die Boxplots mal hier ein. Sinnvoll wäre es wahrscheinlich, anhand der Plots einzuschätzen zu versuchen, ob so was wie ein linearer Zusammenhang besteht.

LG,
Bernhard

[stumper77]

Hallo Bernhard,

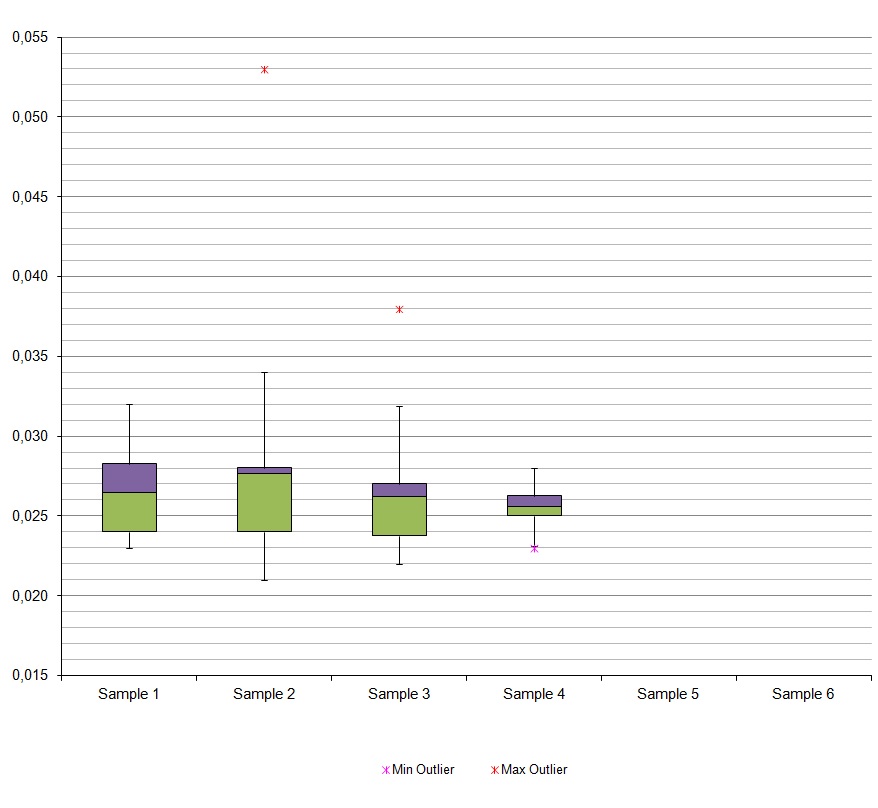
danke für deine Antwort. Ich hab je Konfiguration 20 Messwerte erhalten. Eine alleinige grafische Bewertung ist nicht ausreichend hab ich gelesen und soll somit immernoch rechnerisch dargestellt werden.

LG

[bele]

Hallo stumper,

sind das 4 verschiedene Einstellungen in einer bestimmten Reihenfolge oder ungeordnet? Wenn ungeordnet, dann schlage ich einen Kruskall-Wallis-Test vor mit der Frage, ob die vier Gruppen sich überhaupt voneinander unterscheiden:
http://de.wikipedia.org/wiki/Kruskal-Wallis-Test

Je nach Ergebnis dann weiter.

LG,
Bernhard

PS: Von der Ablehnung der Normalverteilung bin ich noch nicht so überzeugt wie Du...

[bele]

Hier mal zwanzig zufällige Boxplots, Daten jeweils aus streng normalverteilten Grundgesamtheiten gezogen.

Code: Alles auswählen

daten <- data.frame(werte=rnorm(400),gruppe=gl(20,20))
boxplot(werte~gruppe, data=daten, main="n je 20 und normalverteilt")


[stumper77]

Hallo Bernhard,

also das im Diagramm sind 4 Einstellungen mit je 20 Messdaten und der Median als Box Plot dargestellt. Wie vergeleiche ich die Einstellungen am besten miteinander? Laut der Grafik kann man ja schon einen Unterschied im Range sehen und somit auf eine bessere Reproduzierbarkeit schließen, oder ?!

Viele Grüße
Tim

[bele]

Nein, in der Grafik steckt das m. E. nicht drin. Kann Dein Statistikprogramm Boxplots mit "Notches", also seitlichen Kerben, wie hier http://www.statmethods.net/graphs/images/boxplot2.jpg oder hier: http://www.mathworks.de/help/stats/boxplot2.gif ?

Die könnten auf der grafischen Seite bei der Entscheidung helfen, ob es Unterschiede gibt. Ansonsten ist der Nachweis von Unterschieden die Stärke der "rechnerischen" Seite.

Ich muss noch mal Fragen, ob Deine 4 Einstellungen eine bestimmte Reihenfolge haben. Ist irgendwas an Sample1 kleiner eingestellt als bei Sample 2 und bei Sample 2 kleiner als bei Sample 3 oder sind das vier verschiedene Einstellungen ohne Reihenfolge? Falls ohne Reihenfolge, dann hilft Dir ein Kruskall-Wallis-Test bei der Frage, ob überhaupt Unterschiede da sind. Falls nein, dann bist Du fertig. Falls ja, dann kann man mit mit Wilcoxon-Tests die einzelnen Einstellungen paarweise vergleichen.

LG,
Bernhard

[stumper77]

Leider, kann ich das mit den Einkerbungen nicht machen...

Sample 1 und Sample 2 sind ein anderes Messobjekt als Sample 3 und 4.

Die Einstellungen unterscheiden sich in der Genauigkeit der Voreinstellung der Maschine. Sample 1 und 3 ist normal eingestellt per Augenmaß und Sample 2 und 4 ist sehr präzise eingestellt.

[stumper77]

P.S. was ist das m.E.?

[bele]

Gut, dann schau jetzt mal in Deiner Software, ob die den Kruskall-Wallis-Test und ob die den Wilcoxon-Rangsummentest kann.

"m. E." heißt meines Erachtens. Ob die Boxplots echte Unterschiede zeigen oder nur zufällig etwas verschieden sind ist immer auch eine Frage des subjektiven Erachtens. Genau deshalb musst Du Statistik rechnen.