Hallo liebe Community,
ich hätte eine Frage zum Verständnis des Signifikanzniveaus als obere Grenze des Fehler 1. Art.
Diese obere Grenze gilt ja nur bei zweiseitigen Hypothesentests, bei einseitigen ist Alpha = dem Fehler 1. Art.
Angenommen es liegt ein rechtsseitiger einfacher t-Test vor und es wurde ein hypothetischer Parameter festgelegt zur Abgrenzung von H0 und H1. Nun könnte es sein, dass der wahre Parameter mü kleiner ist als der hypothetische, was immer noch zur Annahme von H0 führen würde.
Ist jetzt der Fehler 1. Art deswegen kleiner, weil die Verteilung der Teststatistik sich ändert im Vergleich zur Verteilung der Teststatistik mit dem hypoth. Parameter, sodass der Ablehnungsbereich jetzt eine Wahrscheinlichkeitsmasse überdeckt kleiner als dem Signifikanzniveau?
Liebe Grüße
Max
Signifikanzniveau als Maximum des Fehler 1. Art
Thema bewerten: 




 • 5 Beiträge
• Seite 1 von 1
• 5 Beiträge
• Seite 1 von 1
- Schulze
- Grünschnabel

- Beiträge: 3
- Registriert: Do 25. Mär 2021, 17:16
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Signifikanzniveau als Maximum des Fehler 1. Art
Hallo Max,
wilkommen im Forum. Ich glaube, Du hast die richtige Intuition aber benutzt die falsche Sprache.
Das verstehe ich nicht, aber klar ist, dass Alpha immer eine Obergrenze darstellt. Egal ob ein- oder zweiseitiger Test.
Man müsste überlegen, ob diese Formulierung in der Bayes-Statistik passt. In der Nullhypothesentestung gibt es keinen hypothetischen Parameter. Der wahre Mittelwert ist eine feste Größe. Er bleibt zwar unbekannt aber es werden keine Hypothesen über ihn aufgestellt. Der Vergleichswert aus der Nullhypothese ist bekannt und wird in Formeln eingesetzt, ist also nichts hypothetisches sondern etwas sehr konkretes. Klar könnte es sein, dass der wahre Mittelwert kleiner ist als der Vergleichswert, aber Bedeutung erhält dieser Satz wahrscheinlich erst wenn man spezifiziert, ob das dann im Sinne Deiner Hypothese oder entgegen Deiner Hypothese ist. Ich glaube Du meinst: Wenn wir mit der Nullhypothese testen, dass der wahre Mittelwert kleiner oder gleich 0 ist, dann wird diese Nullhyothese auch dann nicht verworfen, wenn der beobachtete Mittelwert weit kleiner als Null ist. Richtig verstanden?
Der p-Wert ist kleiner, weil ich nicht mehr ein Konfidenzintervall betrachte, dass symmetrisch um 0 liegt sondern eines, dass bei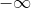 anfängt und deshalb eine kleinere rechte Grenze hat. Es wird also eine andere Fläche unter der Kurve für die Wahrscheinlichkeit der Daten/ie Likelihood unter der Nullhypothese betrachtet.
anfängt und deshalb eine kleinere rechte Grenze hat. Es wird also eine andere Fläche unter der Kurve für die Wahrscheinlichkeit der Daten/ie Likelihood unter der Nullhypothese betrachtet.
Hilft das?
LG,
Bernhard
wilkommen im Forum. Ich glaube, Du hast die richtige Intuition aber benutzt die falsche Sprache.
Schulze hat geschrieben:ich hätte eine Frage zum Verständnis des Signifikanzniveaus als obere Grenze des Fehler 1. Art.
Diese obere Grenze gilt ja nur bei zweiseitigen Hypothesentests, bei einseitigen ist Alpha = dem Fehler 1. Art.
Das verstehe ich nicht, aber klar ist, dass Alpha immer eine Obergrenze darstellt. Egal ob ein- oder zweiseitiger Test.
Angenommen es liegt ein rechtsseitiger einfacher t-Test vor und es wurde ein hypothetischer Parameter festgelegt zur Abgrenzung von H0 und H1. Nun könnte es sein, dass der wahre Parameter mü kleiner ist als der hypothetische, was immer noch zur Annahme von H0 führen würde.
Man müsste überlegen, ob diese Formulierung in der Bayes-Statistik passt. In der Nullhypothesentestung gibt es keinen hypothetischen Parameter. Der wahre Mittelwert ist eine feste Größe. Er bleibt zwar unbekannt aber es werden keine Hypothesen über ihn aufgestellt. Der Vergleichswert aus der Nullhypothese ist bekannt und wird in Formeln eingesetzt, ist also nichts hypothetisches sondern etwas sehr konkretes. Klar könnte es sein, dass der wahre Mittelwert kleiner ist als der Vergleichswert, aber Bedeutung erhält dieser Satz wahrscheinlich erst wenn man spezifiziert, ob das dann im Sinne Deiner Hypothese oder entgegen Deiner Hypothese ist. Ich glaube Du meinst: Wenn wir mit der Nullhypothese testen, dass der wahre Mittelwert kleiner oder gleich 0 ist, dann wird diese Nullhyothese auch dann nicht verworfen, wenn der beobachtete Mittelwert weit kleiner als Null ist. Richtig verstanden?
Ist jetzt der Fehler 1. Art deswegen kleiner, weil die Verteilung der Teststatistik sich ändert im Vergleich zur Verteilung der Teststatistik mit dem hypoth. Parameter, sodass der Ablehnungsbereich jetzt eine Wahrscheinlichkeitsmasse überdeckt kleiner als dem Signifikanzniveau?
Der p-Wert ist kleiner, weil ich nicht mehr ein Konfidenzintervall betrachte, dass symmetrisch um 0 liegt sondern eines, dass bei
Hilft das?
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Signifikanzniveau als Maximum des Fehler 1. Art
Hallo Bernhard,
vielen Dank für deine schnelle Antwort!
In meiner Statistikvorlesung wurde dies so beschrieben. Siehe auch https://de.wikipedia.org/wiki/Fehler_1._und_2._Art Abschnitt 2 unten.
Dann habe ich mich missverständlich ausgedrückt. Mit dem hypothetischen Wert meine ich den Vergleichswert.
Genau so meine ich es
Nach langem überlegen habe ich es verstanden, glaube ich zumindest. Wenn das KI einseitig nach unendlich geöffnet wird, ist die Wahrscheinlichkeit, dass es den Parameter umschließt höher als 1-alpha, was auch heißt dass die Gegenwahrscheinlichkeit kleiner als alpha ist, korrekt? Das würde auch bedeuten, dass die Grenze für den kritischen Bereich im Kontext der Verteilung der Teststatistik dann weiter rechts liegt.
Liebe Grüße
Max
vielen Dank für deine schnelle Antwort!
Das verstehe ich nicht, aber klar ist, dass Alpha immer eine Obergrenze darstellt. Egal ob ein- oder zweiseitiger Test.
In meiner Statistikvorlesung wurde dies so beschrieben. Siehe auch https://de.wikipedia.org/wiki/Fehler_1._und_2._Art Abschnitt 2 unten.
Der Vergleichswert aus der Nullhypothese ist bekannt und wird in Formeln eingesetzt, ist also nichts hypothetisches sondern etwas sehr konkretes.
Dann habe ich mich missverständlich ausgedrückt. Mit dem hypothetischen Wert meine ich den Vergleichswert.
Wenn wir mit der Nullhypothese testen, dass der wahre Mittelwert kleiner oder gleich 0 ist, dann wird diese Nullhyothese auch dann nicht verworfen, wenn der beobachtete Mittelwert weit kleiner als Null ist. Richtig verstanden?
Genau so meine ich es
Der p-Wert ist kleiner, weil ich nicht mehr ein Konfidenzintervall betrachte, dass symmetrisch um 0 liegt sondern eines, dass bei anfängt und deshalb eine kleinere rechte Grenze hat. Es wird also eine andere Fläche unter der Kurve für die Wahrscheinlichkeit der Daten/ie Likelihood unter der Nullhypothese betrachtet.
Nach langem überlegen habe ich es verstanden, glaube ich zumindest. Wenn das KI einseitig nach unendlich geöffnet wird, ist die Wahrscheinlichkeit, dass es den Parameter umschließt höher als 1-alpha, was auch heißt dass die Gegenwahrscheinlichkeit kleiner als alpha ist, korrekt? Das würde auch bedeuten, dass die Grenze für den kritischen Bereich im Kontext der Verteilung der Teststatistik dann weiter rechts liegt.
Liebe Grüße
Max
- Schulze
- Grünschnabel

- Beiträge: 3
- Registriert: Do 25. Mär 2021, 17:16
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Signifikanzniveau als Maximum des Fehler 1. Art
Hi!
Prima, dann haben wir einen wichtigen Punkt geklärt.
Ich glaube auch, dass Du es wahrscheinlich verstanden hast, aber auch hier hadere ich mit Deinen Formulierungen. "dass es den Parameter umschließt". Wenn Du hier den wahren Parameter meinst, das wird in der Nullhypothesentestung nicht gefragt, ob der im Konfidenzintervall liegt. Wenn Du den "hypothetischen Parameter" oder den beobachteten meinst, dann musst Du nochmal genau sagen, von welchem Konfidenzintervall Du gerade sprichst. Auch ist mir nicht klar, ob bei Deiner "einseitigen Öffnung des KI nach unendlich" die andere Grenze konstant bleibt oder auch verschoben wird. Sie muss ebenfalls verschoben werden wenn es ein 95%_KI bleiben soll. Leider kann man hier keine Grafiken hochladen und sprachlich kommen wir beide heute wohl nicht so genau zusammen aber wenn Du jetzt das Gefühl hast, den Test besser zu vestehen, dann ist ja alles golden.
LG,
Bernhard
Schulze hat geschrieben:Wenn wir mit der Nullhypothese testen, dass der wahre Mittelwert kleiner oder gleich 0 ist, dann wird diese Nullhyothese auch dann nicht verworfen, wenn der beobachtete Mittelwert weit kleiner als Null ist. Richtig verstanden?
Genau so meine ich es
Prima, dann haben wir einen wichtigen Punkt geklärt.
Schulze hat geschrieben:Der p-Wert ist kleiner, weil ich nicht mehr ein Konfidenzintervall betrachte, dass symmetrisch um 0 liegt sondern eines, dass bei anfängt und deshalb eine kleinere rechte Grenze hat. Es wird also eine andere Fläche unter der Kurve für die Wahrscheinlichkeit der Daten/ie Likelihood unter der Nullhypothese betrachtet.
Nach langem überlegen habe ich es verstanden, glaube ich zumindest. Wenn das KI einseitig nach unendlich geöffnet wird, ist die Wahrscheinlichkeit, dass es den Parameter umschließt höher als 1-alpha, was auch heißt dass die Gegenwahrscheinlichkeit kleiner als alpha ist, korrekt? Das würde auch bedeuten, dass die Grenze für den kritischen Bereich im Kontext der Verteilung der Teststatistik dann weiter rechts liegt.
Ich glaube auch, dass Du es wahrscheinlich verstanden hast, aber auch hier hadere ich mit Deinen Formulierungen. "dass es den Parameter umschließt". Wenn Du hier den wahren Parameter meinst, das wird in der Nullhypothesentestung nicht gefragt, ob der im Konfidenzintervall liegt. Wenn Du den "hypothetischen Parameter" oder den beobachteten meinst, dann musst Du nochmal genau sagen, von welchem Konfidenzintervall Du gerade sprichst. Auch ist mir nicht klar, ob bei Deiner "einseitigen Öffnung des KI nach unendlich" die andere Grenze konstant bleibt oder auch verschoben wird. Sie muss ebenfalls verschoben werden wenn es ein 95%_KI bleiben soll. Leider kann man hier keine Grafiken hochladen und sprachlich kommen wir beide heute wohl nicht so genau zusammen aber wenn Du jetzt das Gefühl hast, den Test besser zu vestehen, dann ist ja alles golden.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Signifikanzniveau als Maximum des Fehler 1. Art
danke für die Ausführungen, ich denke, das passt schon so. 
Liebe Grüße
Max
Liebe Grüße
Max
- Schulze
- Grünschnabel

- Beiträge: 3
- Registriert: Do 25. Mär 2021, 17:16
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 5 Beiträge
• Seite 1 von 1
• 5 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 4 Gäste


