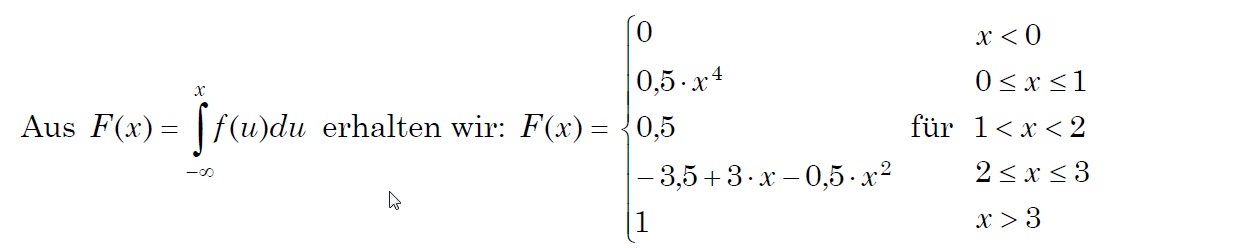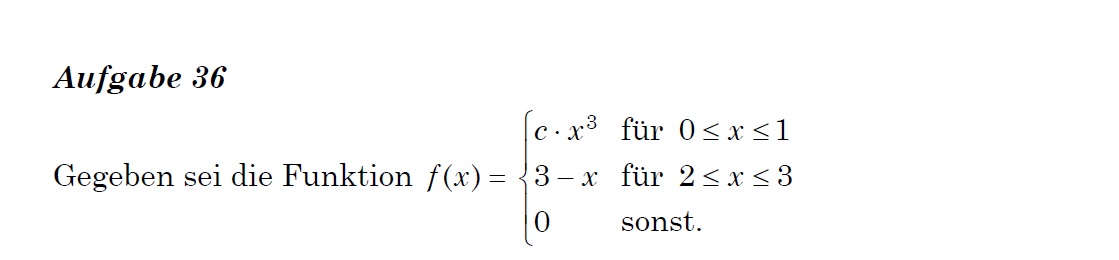Verteilungsfunktion
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Verteilungsfunktion
Hallo! Ich habe eine Frage bezüglich der Verteilungsfunktion einer stetigen Zufallsvariable. Ich glaube, mir sind die Eigenschaften der Funktion bekannt, aber offensichtlich gibt es etwas das ich nicht verstehe. Ich habe stundelang versucht die Verteilungsfunktion anhand der Dichte zu berechnen, aber es klappt immer noch nicht. Ich wäre dankbar, wenn jemand mir erklären kann, wie wir auf das folgende Ergebnis kommen. Die "c'' Konstante habe ich schon berechnet und es ergibt sich 2. Ich habe auch die Lösung hochgeladen. Danke im Voraus. 

- Eva93
- Grünschnabel

- Beiträge: 2
- Registriert: Do 25. Jul 2013, 11:08
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Verteilungsfunktion
Hallo Eva,
leider schreibst Du nicht, was Du nicht verstehst. Du musst die Funktion von links nach rechts integrieren. Bis x=0 ist die Funktion f = 0. Also ist auch die Fläche unter der Kurve immer 0. Damit ist auch die erste Zeile von F(x) schon erklärt. Von x=0 bis x=1 ist f(x)=2*x^3 Die Stammfunktion davon ist F(x)=0,5*x^4. Damit ist die zweite Zeile von F(x) erklärt. Zwischen x=1 und x=2 ist f(x) schon wieder 0. Also steigt die Fläche unter ihrer Kurve in diesem Bereich nicht an und ist so groß, wie die Fläche links davon, also so groß wie F(1). F(1) = 0,5*1^4 = 2 und damit ist die dritte Zeile von F(x) erklärt. Kommst Du soweit mit?
LG,
Bernhard
leider schreibst Du nicht, was Du nicht verstehst. Du musst die Funktion von links nach rechts integrieren. Bis x=0 ist die Funktion f = 0. Also ist auch die Fläche unter der Kurve immer 0. Damit ist auch die erste Zeile von F(x) schon erklärt. Von x=0 bis x=1 ist f(x)=2*x^3 Die Stammfunktion davon ist F(x)=0,5*x^4. Damit ist die zweite Zeile von F(x) erklärt. Zwischen x=1 und x=2 ist f(x) schon wieder 0. Also steigt die Fläche unter ihrer Kurve in diesem Bereich nicht an und ist so groß, wie die Fläche links davon, also so groß wie F(1). F(1) = 0,5*1^4 = 2 und damit ist die dritte Zeile von F(x) erklärt. Kommst Du soweit mit?
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5928
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1403 mal in 1389 Posts
Re: Verteilungsfunktion
Hallo,
Ja, sorry, eigentlich habe ich nicht erwähnt, was genau mir nicht klar ist. Ich bin schon auf das Ergebnis gekommen. Das Problem bestand in dem Intervall 2=<x<=3. Ich habe diese Eigenschaft des Integrals vergessen: nämlich, dass man int(3-x)dx als Differenz: int (3)dx - int(x)dx betrachten kann. Damit haben sich die Vorzeichen verwechselt. Bis dorthin bin ich zurechtgekommen. Es kommt aber noch eine weitere Aufgabe, wo ich INT (x.(3-x))dx habe. Soweit ich weiß, wenden wir die partielle Integration an. Ich komme aber wieder nicht auf die richtige Lösung.
LG,
Eva
Ja, sorry, eigentlich habe ich nicht erwähnt, was genau mir nicht klar ist. Ich bin schon auf das Ergebnis gekommen. Das Problem bestand in dem Intervall 2=<x<=3. Ich habe diese Eigenschaft des Integrals vergessen: nämlich, dass man int(3-x)dx als Differenz: int (3)dx - int(x)dx betrachten kann. Damit haben sich die Vorzeichen verwechselt. Bis dorthin bin ich zurechtgekommen. Es kommt aber noch eine weitere Aufgabe, wo ich INT (x.(3-x))dx habe. Soweit ich weiß, wenden wir die partielle Integration an. Ich komme aber wieder nicht auf die richtige Lösung.
LG,
Eva
- Eva93
- Grünschnabel

- Beiträge: 2
- Registriert: Do 25. Jul 2013, 11:08
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Verteilungsfunktion
Hallo Eva93,
Meinst du vielleicht\,dx?) Du Könntest das Integral mittels der Produktregel der Integrationsrechnung bestimmen. Ich würd dir empfehlen, dass du die Klammern ausmultiplizierst und dann
Du Könntest das Integral mittels der Produktregel der Integrationsrechnung bestimmen. Ich würd dir empfehlen, dass du die Klammern ausmultiplizierst und dann  integrierst. Die partielle Integration wird in der mehrdimensionalen Analysis verwendet. Hierbei wird eine mehrdimensionale Funktion z.B.
integrierst. Die partielle Integration wird in der mehrdimensionalen Analysis verwendet. Hierbei wird eine mehrdimensionale Funktion z.B. =x+y) über eine Variable integriert, wobei die übrigen anderen wie konstanten behandelt werden.
über eine Variable integriert, wobei die übrigen anderen wie konstanten behandelt werden.
Im Übrigen:
Wir sind ja alle Statistiker
und wissen, dass Wahrscheinlichkeiten zwischen 0 und 1 liegen sollten, vergleiche Kolmogorow-Axiome. Wobei ich annehme, dass es sich hier um einen Tippfehler handelt. Da ja auch gilt
Liebe Grüße
Eva93 hat geschrieben: Es kommt aber noch eine weitere Aufgabe, wo ich INT (x.(3-x))dx habe. Soweit ich weiß, wenden wir die partielle Integration an.
Meinst du vielleicht
Im Übrigen:
bele hat geschrieben:F(1) = 0,5*1^4 = 2
Wir sind ja alle Statistiker
und wissen, dass Wahrscheinlichkeiten zwischen 0 und 1 liegen sollten, vergleiche Kolmogorow-Axiome. Wobei ich annehme, dass es sich hier um einen Tippfehler handelt. Da ja auch gilt
Liebe Grüße
"Essentially, all models are wrong, but some are useful. However, the approximate nature of the model must always be borne in mind.",
Box, George E. P.; Draper, Norman R. (1987). Empirical Model-Building and Response Surfaces, p. 424, Wiley.
Box, George E. P.; Draper, Norman R. (1987). Empirical Model-Building and Response Surfaces, p. 424, Wiley.
- Frequentist
- User

- Beiträge: 33
- Registriert: Sa 27. Jul 2013, 14:52
- Danke gegeben: 3
- Danke bekommen: 4 mal in 4 Posts
Re: Verteilungsfunktion
Frequentist hat geschrieben:Wobei ich annehme, dass es sich hier um einen Tippfehler handelt. Da ja auch gilt
Tippfehler? Schön wär's. So was glaub ich in dem Moment wahrscheinlich selbst. Das Umformen von 0,5 zu
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5928
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1403 mal in 1389 Posts
Re: Verteilungsfunktion
Stimmt. Wenn gelten würde  , dann würde das Ergebnis, zumindest arithmetisch, wieder passen.
, dann würde das Ergebnis, zumindest arithmetisch, wieder passen. 
Liebe Grüße
F.
Liebe Grüße
F.
"Essentially, all models are wrong, but some are useful. However, the approximate nature of the model must always be borne in mind.",
Box, George E. P.; Draper, Norman R. (1987). Empirical Model-Building and Response Surfaces, p. 424, Wiley.
Box, George E. P.; Draper, Norman R. (1987). Empirical Model-Building and Response Surfaces, p. 424, Wiley.
- Frequentist
- User

- Beiträge: 33
- Registriert: Sa 27. Jul 2013, 14:52
- Danke gegeben: 3
- Danke bekommen: 4 mal in 4 Posts
Re: Verteilungsfunktion
Dann muss ich mal eine Wasserwaage suchen. Vielleicht habe ich den Monitor etwas schief stehen...
Am Ende ist es dann kein arithmetisches sondern ein geometrisches Problem.
Am Ende ist es dann kein arithmetisches sondern ein geometrisches Problem.
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5928
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1403 mal in 1389 Posts
Re: Verteilungsfunktion
Auch wenn mein Kommentar nun nicht fachlicher Natur entspricht:
Der war super!
bele hat geschrieben:Dann muss ich mal eine Wasserwaage suchen. Vielleicht habe ich den Monitor etwas schief stehen...
Am Ende ist es dann kein arithmetisches sondern ein geometrisches Problem.
Der war super!
"Essentially, all models are wrong, but some are useful. However, the approximate nature of the model must always be borne in mind.",
Box, George E. P.; Draper, Norman R. (1987). Empirical Model-Building and Response Surfaces, p. 424, Wiley.
Box, George E. P.; Draper, Norman R. (1987). Empirical Model-Building and Response Surfaces, p. 424, Wiley.
- Frequentist
- User

- Beiträge: 33
- Registriert: Sa 27. Jul 2013, 14:52
- Danke gegeben: 3
- Danke bekommen: 4 mal in 4 Posts
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 19 Gäste