STATISTIK-FORUM.de

[simpson25]

Hallo zusammen,

schreibe aktuell meine Abschlussarbeit und stehe vor folgendem Problem:

Ich habe eine Zeitreihe von 48 Monaten mit Verkäufen eines bestimmten Produktes. Jeder Monat steht dabei für eine bestimmte Menge, die das Produkt verkauft wurde. Nun habe ich aus diesen Werten den Korrelationskoeffizienten nach Bracais-Pearson gebildet, um bspw. einen Trend für die Zukunft abgeben zu können, ob in den nächsten Jahren ein höherer oder sinkender Verkauf zu erwarten ist.

Ist dies eurer Meinung nach mit dieser Methode möglich ( oder gibt es eine bessere Möglichkeit eine solche Prognose abzubilden?

Vielen Dank für Eure Hilfe!

[bele]

Hi,

ich verstehe weder, was Du mit was korreliert hast noch, wie Du aus einem Korrelationskoeffizienten eine Prognose errechnen willst. Vielleicht kannst Du das etwas präziser erklären?

LG,
Bernhard

[simpson25]

Die Zeitreihe ist beispielsweise:

Monat 1: 100 Stk.
Monat 2: 110 Stk.
Monat 3: 120 Stk.
.
.
.
Monat 48: 359

Nun will ich eben sehen, ob über die Monate hinweg ein Trend zusehen ist. x und y wären hier die Monate und Verkäufe. Denke das Verfahren ist überhaupt nicht auf mein Problem anwendbar, da es weder normalverteilt ist, noch in dem Sinne zwei Variablen besitzt.

Welche(s) Verfahren würde(n) sich für das Problem besser eignen?

[bele]

Zeitreihenanalyse ist kein leichtes Thema, dass man schnell mal in einem Post erklärt. Vielleicht ist das ein Einstieg für Dein Problem:
http://de.wikipedia.org/wiki/Trendmodell

LG,
Bernhard

[simpson25]

Meine bisherige Methode ist daher definitiv falsch?

[bele]

Jain. Du hast Monatszahl und Verkaufszahl korreliert. Die Monatszahl wird immer immer größer und wenn sie positiv mit den Verkaufszahlen korreliert, dann werden auch die Verkaufszahlen im Laufe der Zeit größer. Das stimmt soweit schon. Und wenn Du statt Bravais-Pearson auf Spearman ausweichst musst Du Dir auch um Normalverteilung etc. keine Gedanken machen. Aber: Du steckst in einer Sackgasse. Die Korrelationsrechnung besagt, dass die Verkaufszahlen mit den Monaten steigen. Sie beinhaltet aber keine Informationen darüber, wie schnell sie steigen. Daher ist auch keine Vorhersage für die Zukunft damit möglich.

Wenn Du stattdessen im einfachsten Fall eine lineare Regression rechnest, dann erhälst Du eine Formel der Art Verkaufszahl = Konstante1 mal Monat plus Konstante2.
Damit sind dann auf einmal Vorhersagen möglich. Wenn Du komplexere Modelle, z. B. mit jahreszeitlichen Schwankungen etc. rechnest, dann werden Deine Vorhersagen vielleicht genauer (wenn es z. B. jahreszeitliche Schwankungen gibt).

Kannst Du vielleicht mal eine Grafik mit Deinen Werten hochladen? Sowas wie Monat auf der x-Achse, Verkaufszahl auf der y-Achse?

[simpson25]

So wie ich die Rangkorrelation verstanden habe, bringt er doch meine Verkäufe in eine neue Reihenfolge, sodass doch nicht mehr der Trend "in der richtigen Reihenfolge berücksichtigt wird, also so wie sie in den einzelnen Monaten angefallen sind oder irre ich mich?

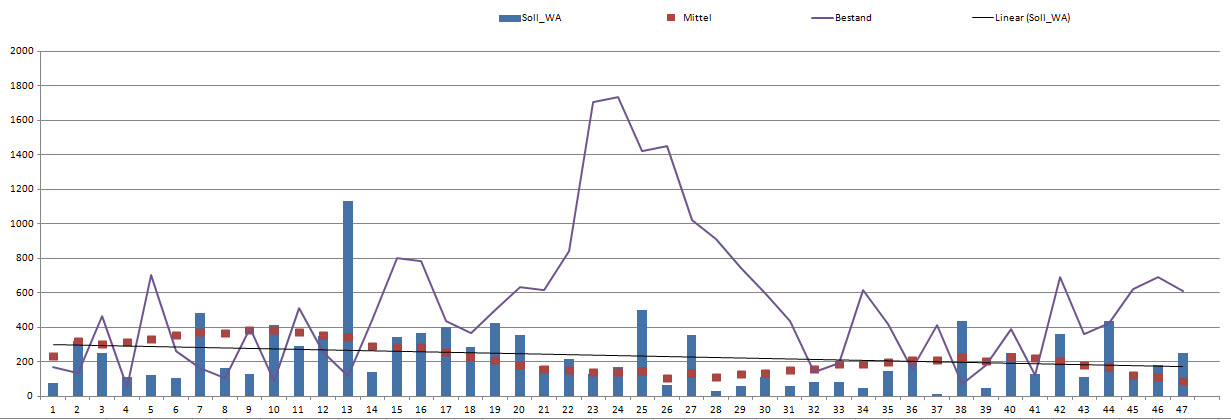
Ich habe mal einen Verlauf hoch geladen. Dabei spiegelt der Soll_WA die Verkäufe wieder (y-Achse = verkaufte Stück, x-Achse = Monate)

17.06.jpg (105.25 KiB) 2621-mal betrachtet

Wenn ich das Verfahren auf die lineare Regression ändere, gibt es da eine Möglichkeit die Steigung zu normieren? Ich möchte einzelne Produkte miteinander vergleichen und da wäre eine Normierung wie sie bei der Korrelation vorhanden ist, von großem Vorteil.[

[bele]

Hallo Simpson,

ich glaube, dass Du Dich in Bezug auf die Rangkorrelation irrst. Das Umsortieren ist doch nur ein Detail in der Bestimmung des Korrelationsmaßes. Korrelation bedeutet weiterhin: Wird das eine größer, dass im Allgemeinen auch das andere.

Die blauen Balken in Deiner Grafik sind das, worüber Du Prognosen machen möchtest? Das sieht ziemlich zufällig aus und wird sich schwer prognostizieren lassen. Wenn überhaupt, dann würde ich eher an einen abfallenden Trend als an einen ansteigenden glauben, aber das kann man ja rechnen.

Ich verstehe, ehrlich gesagt, nicht, was Du mit "Normieren der Steigung" meinst. Die Steigung als objektive Zahl herauszufinden ist das Ziel der Regression. Da will man doch möglichst wenig an dieser Steigung ändern. Geht es denn nun um die Prognose oder um den Vergleich verschiedener Produkte?

LG,
Bernhard

[simpson25]

Die Prognose hat eine hohe Volatilität, doch ist bei den meisten Materialien ein Trend zu erkennen. Ich habe die Rangkorrelation ebenfalls durchgespielt und die Werte schwanken zwischen 03 und 0,6, was keine eindeutige Korrelation ausgibt.
Werde diesen Ansatz vermutlich verwerfen und mich auf die Regression konzentrieren.

Die Produkte werden nicht direkt miteinander verglichen. Die Trenderkennung (1. steigt; 2. sinkt 3. schwankt um MW) soll bei einer späteren unabhängigen Bedarfsermittlung helfen, damit für die Zukunft bspw. 20% mehr oder weniger eingeplant wird.

Vielleicht habe ich mich mit der Normierung der Steigung falsch ausgedrückt. Ich möchte eben einen normierten Wert ermitteln, der mir erlaubt, eine Grenze bilden zu können, bspw. Materialbedarf steigt und Material schwankt um Mittelwert.

Eine Idee, wie ich das umsetzen kann?

[bele]

Wenn beta nicht signifikant, dann kein Nachweis eines Trends -> eher von konstantem Materialbedarf ausgehen oder Datengrundlage reicht nicht aus
Wenn beta signifikant und negativ -> Materialbedarf sinkt, um wieviel, das schätzt der Betrag von beta
Wenn beta signifikant und positiv -> Materialbedarf steigt, um wieviel, das schätzt der Betrag von beta