Ausgangspunkt der Aufgabe ist ein Packungsinhalt von 100 Stück mit einem gegebenen Erwartungswert und Standardabweichung (es liegt eine Normalverteilung vor). Bekanntlich entspricht bei einer Normalverteilung das Mittel dem Modus bzw. dem Median. Nun ist gefragt, wie dieses Mittel verteilt ist und wie groß die Wahrscheinlichkeit für einen bestimmten Mittelwert ist. Mir fehlt gerade die Idee, wie ich den Rechenweg beschreiten soll. Falls mir jemand helfen könnte, wäre das fantastisch.
VG
Arith. Mittel bei Normalverteilung
Thema bewerten: 




 • 2 Beiträge
• Seite 1 von 1
• 2 Beiträge
• Seite 1 von 1
- Henry90
- Einmal-Poster

- Beiträge: 1
- Registriert: Do 25. Apr 2013, 15:26
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Arith. Mittel bei Normalverteilung
Hallo Henry,
betrachten wir das arithmetische von normalverteilten Zufallsvariablen. Hierbei handelt es sich um die Summe jener Zufallsvariablen multipliziert mit dem Gewicht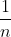 , mit
, mit  Anzahl der Zufallsvariablen. Vermutlich wird in deinen Unterlagen etwas über die Verteilung der Summe normalverteilter Zufallsvariablen und die Verteilung von linearen Transformationen normalverteilter Zufallsvariablen stehen. Bei linearen Transformationen handelt es sich um Zufallsvariablen multipliziert mit einer konstanten
Anzahl der Zufallsvariablen. Vermutlich wird in deinen Unterlagen etwas über die Verteilung der Summe normalverteilter Zufallsvariablen und die Verteilung von linearen Transformationen normalverteilter Zufallsvariablen stehen. Bei linearen Transformationen handelt es sich um Zufallsvariablen multipliziert mit einer konstanten  und addiert um eine konstante
und addiert um eine konstante 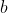 .
.
Beim arithmetischen Mittel von normalverteilten Zufallsvariablen handelt es sich somit um die Summe von linear transformierten normalverteilten Zufallsvariablen. Hast du daraufhin die Verteilung des arithmetischen Mittels bestimmt, so sollte das berechnen einer bestimmten Wahrscheinlichkeit kein Problem mehr sein.
Gruß
a
betrachten wir das arithmetische von normalverteilten Zufallsvariablen. Hierbei handelt es sich um die Summe jener Zufallsvariablen multipliziert mit dem Gewicht
Beim arithmetischen Mittel von normalverteilten Zufallsvariablen handelt es sich somit um die Summe von linear transformierten normalverteilten Zufallsvariablen. Hast du daraufhin die Verteilung des arithmetischen Mittels bestimmt, so sollte das berechnen einer bestimmten Wahrscheinlichkeit kein Problem mehr sein.
Gruß
a
- aziz
- Danke gegeben:
- Danke bekommen: mal in Post
Thema bewerten: 




 • 2 Beiträge
• Seite 1 von 1
• 2 Beiträge
• Seite 1 von 1
Zurück zu Mittelwert, Standardabweichung & Co.
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 4 Gäste


