Hallo allerseits!
Ich hätte mal eine Frage zur Addition von Verteilungen
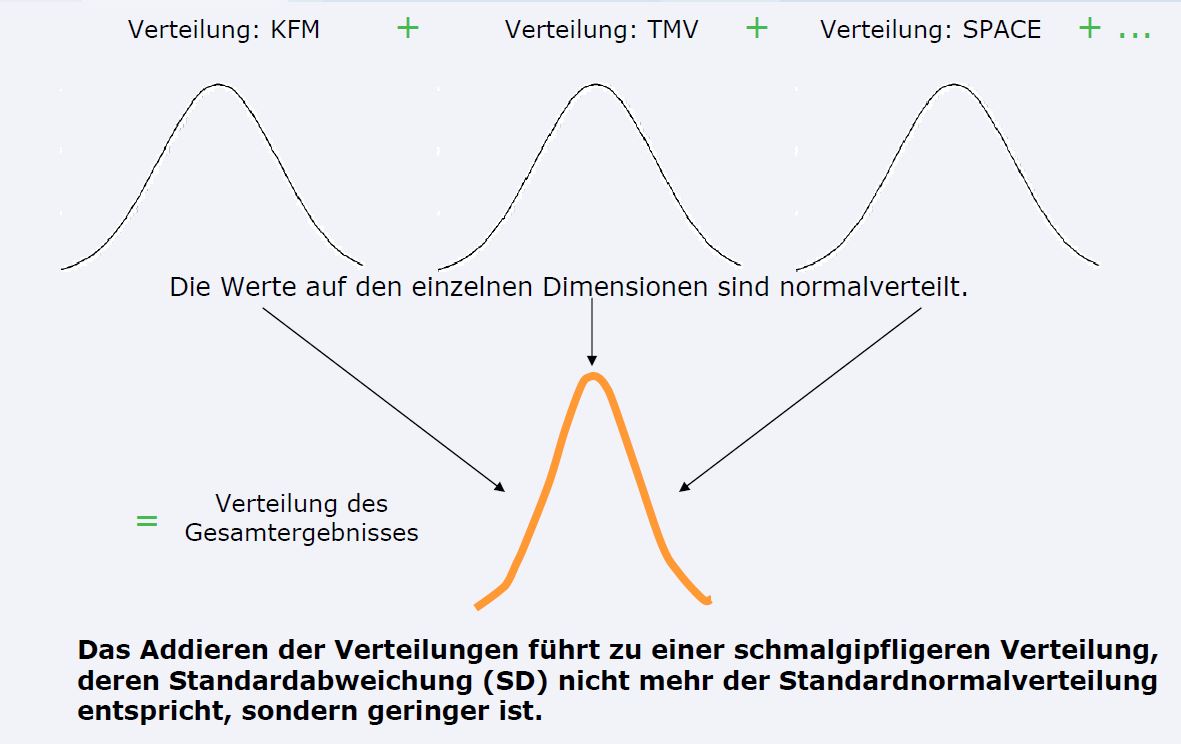
Merkmal 1, Merkmal 2 und Merkmal 3 sind normalverteilt und sollen als Gesamtergebnis verrechnet werden.
Dabei sagen mir nun meine Unterlagen: Das Addieren der Verteilungen führt zu einer schmalgipfligen Verteilung, deren SD nicht der StandardNV entspricht, sondern geringer ist.
Ich verstehe nur gerade nicht warum die Addition von 3 NV eine schmalgipflige Verteilung ergeben soll und nicht nur den Mittelwert aus NV1+NV2+NV3 ...also wieder eine NV
Kann mir da zufällig jemand weiterhelfen???
Dazu besteht dann die Notwendigkeit einer Verteilungskorrektur...logisch, um von schmal wieder auf normal zu kommen...
LG; Nick
Verteilungsaddition
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
- NickVanBeat
- Grünschnabel

- Beiträge: 7
- Registriert: Fr 12. Apr 2013, 14:00
- Danke gegeben: 3
- Danke bekommen: 0 mal in 0 Post
Re: Verteilungsaddition
Hallo Nick,
Ich formuliere es noch etwas allgemeiner:
Seien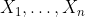 unabhängige normalverteilte Zufallsvariablen mit Erwartungswert
unabhängige normalverteilte Zufallsvariablen mit Erwartungswert 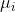 und Varianz
und Varianz 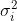 .
.
In Zeichen:, \ i=1,\dots,n) .
.
Dann gilt für die Summe:
)
Ich habe keine Ahnung, was in deinen Unterlagen steht, noch steht oder nicht steht, aber dies gilt im Allgemeinen nicht! Gegenbeispiel:
Seien) . Dann gilt:
. Dann gilt: ) . Deren Varianz bzw. Standardabweichung ist größer der der Standardnormlaverteilung!
. Deren Varianz bzw. Standardabweichung ist größer der der Standardnormlaverteilung!
Gruß
Aziz
NickVanBeat hat geschrieben:Merkmal 1, Merkmal 2 und Merkmal 3 sind normalverteilt und sollen als Gesamtergebnis verrechnet werden.
Ich formuliere es noch etwas allgemeiner:
Seien
In Zeichen:
Dann gilt für die Summe:
NickVanBeat hat geschrieben:Dabei sagen mir nun meine Unterlagen: Das Addieren der Verteilungen führt zu einer schmalgipfligen Verteilung, deren SD nicht der StandardNV entspricht, sondern geringer ist.
Ich habe keine Ahnung, was in deinen Unterlagen steht, noch steht oder nicht steht, aber dies gilt im Allgemeinen nicht! Gegenbeispiel:
Seien
Gruß
Aziz
- aziz
- Danke gegeben:
- Danke bekommen: mal in Post
Re: Verteilungsaddition
Hallo Aziz,
vielen Dank für die Unterstützung...
war am Wochenende leider nicht zuhause...daher jetzt meine Antwort...
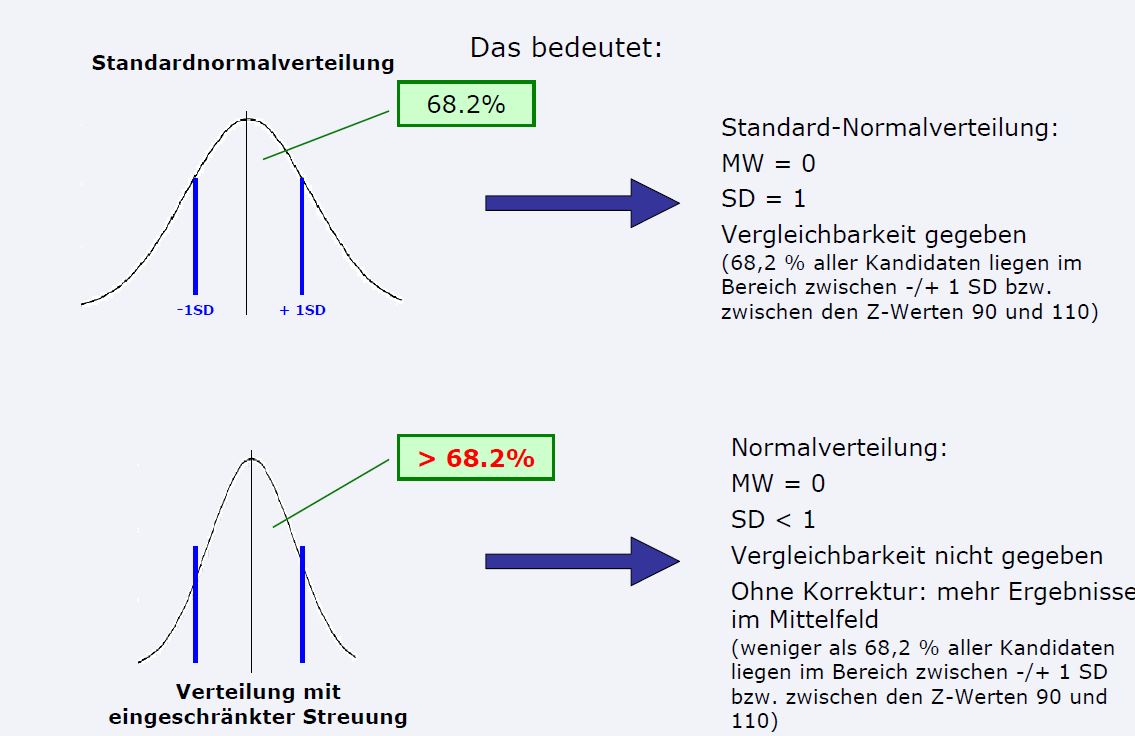
Das zeigen die Unterlagen:
siehe Bild 1 und Bild 2
also kann ich in diesem Fall davon ausgehen, dass das nicht korrekt ist?
(Das Beispiel entstammt inhaltlich der Psychologie...die drei Subtests (Verteilungen) bilden allgemeine und spezifische kognitive Fähigkeiten, sowie Persönlichkeitsmerkmale ab)
mfG; Nick
vielen Dank für die Unterstützung...
war am Wochenende leider nicht zuhause...daher jetzt meine Antwort...
Das zeigen die Unterlagen:
siehe Bild 1 und Bild 2
also kann ich in diesem Fall davon ausgehen, dass das nicht korrekt ist?
(Das Beispiel entstammt inhaltlich der Psychologie...die drei Subtests (Verteilungen) bilden allgemeine und spezifische kognitive Fähigkeiten, sowie Persönlichkeitsmerkmale ab)
mfG; Nick
- NickVanBeat
- Grünschnabel

- Beiträge: 7
- Registriert: Fr 12. Apr 2013, 14:00
- Danke gegeben: 3
- Danke bekommen: 0 mal in 0 Post
Re: Verteilungsaddition
Hallo Nick,
Allgemein gilt obiges.
Das möchte ich nicht in Frage stellen. Leider geht aus dem Beispiel nicht hervor, um welche Verteilungen es sich handelt.
Gruß
Aziz
NickVanBeat hat geschrieben:also kann ich in diesem Fall davon ausgehen, dass das nicht korrekt ist?
Allgemein gilt obiges.
NickVanBeat hat geschrieben:(Das Beispiel entstammt inhaltlich der Psychologie...die drei Subtests (Verteilungen) bilden allgemeine und spezifische kognitive Fähigkeiten, sowie Persönlichkeitsmerkmale ab)
Das möchte ich nicht in Frage stellen. Leider geht aus dem Beispiel nicht hervor, um welche Verteilungen es sich handelt.
Gruß
Aziz
- aziz
- Danke gegeben:
- Danke bekommen: mal in Post
Re: Verteilungsaddition
Die Varianz der Summe zweier normalverteilter Variablen kann
nicht kleiner sein als die einzelnen Varianzen, siehe z.B.
http://en.wikipedia.org/wiki/Sum_of_nor ... _variables
sowohl für den korrelierten (independent) als auch den
unkorrelierten Fall.
Vielleicht geht da was mit der Verteilung von
Stichprobenmittelwerten durcheinander bzw. es geht um
Reliabilität und den Standardfehler oder was auch immer?
Wo stammt denn das her, hat das ein Lehrstuhl herausgegeben?
Mit freundlichen Grüßen
P.
nicht kleiner sein als die einzelnen Varianzen, siehe z.B.
http://en.wikipedia.org/wiki/Sum_of_nor ... _variables
sowohl für den korrelierten (independent) als auch den
unkorrelierten Fall.
Vielleicht geht da was mit der Verteilung von
Stichprobenmittelwerten durcheinander bzw. es geht um
Reliabilität und den Standardfehler oder was auch immer?
Wo stammt denn das her, hat das ein Lehrstuhl herausgegeben?
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11388
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2510 mal in 2494 Posts
Re: Verteilungsaddition
@ Aziz : stimmt, das geht leider nicht hervor...ich kann mir höchstens vorstellen, dass die angenommene Verteilung normalverteilt ist, die tatsächliche abweicht und die Summe der tatsächlichen Verteilung dann schmalgipflich wird...aber das ist nur Spielerei und entbehrt jeder Grundlage ...
@ P. : Das sind Unterlagen, die ich aus meinem Studium an der Universität Bamberg habe...also schon relativ alt, aber die Statistik hat sich ja nicht neu erfunden in den letzten 10 Jahren...Über Reliabilitäten und Standardfehler geht es hier nicht...Die Grundaussage hinter der Gesamtpräsentation ist lediglich die, dass man wenn man mehrere Verteilungen mittelt eine Verteilungskorrektur durchführen muss, damit am Ende mit z-standardisierten Werten weitergearbeitet werden kann...
@ P. : Das sind Unterlagen, die ich aus meinem Studium an der Universität Bamberg habe...also schon relativ alt, aber die Statistik hat sich ja nicht neu erfunden in den letzten 10 Jahren...Über Reliabilitäten und Standardfehler geht es hier nicht...Die Grundaussage hinter der Gesamtpräsentation ist lediglich die, dass man wenn man mehrere Verteilungen mittelt eine Verteilungskorrektur durchführen muss, damit am Ende mit z-standardisierten Werten weitergearbeitet werden kann...
- NickVanBeat
- Grünschnabel

- Beiträge: 7
- Registriert: Fr 12. Apr 2013, 14:00
- Danke gegeben: 3
- Danke bekommen: 0 mal in 0 Post
Re: Verteilungsaddition
Hallo Nick,
Es geht also um den Mittelwert von Normalverteilten bzw. Standardnormalverteilten Zufallsvariablen. Im Falle von unabhängiger Standardnormalverteilten Zufallsvariablen also
unabhängiger Standardnormalverteilten Zufallsvariablen also , \ i=1,\dots n) stimmt das, denn dann gilt:
stimmt das, denn dann gilt:
.)
Gruß
Aziz
NickVanBeat hat geschrieben:Die Grundaussage hinter der Gesamtpräsentation ist lediglich die, dass man wenn man mehrere Verteilungen mittelt eine Verteilungskorrektur durchführen muss, damit am Ende mit z-standardisierten Werten weitergearbeitet werden kann...
Es geht also um den Mittelwert von Normalverteilten bzw. Standardnormalverteilten Zufallsvariablen. Im Falle von
Gruß
Aziz
Zuletzt geändert von aziz am Mo 15. Apr 2013, 19:48, insgesamt 1-mal geändert.
- aziz
- Danke gegeben:
- Danke bekommen: mal in Post
Re: Verteilungsaddition
Alles klar! Recht herzlichen Dank!
- NickVanBeat
- Grünschnabel

- Beiträge: 7
- Registriert: Fr 12. Apr 2013, 14:00
- Danke gegeben: 3
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Zurück zu Mittelwert, Standardabweichung & Co.
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 2 Gäste