Hallo,
da wir uns in der nicht Parametrik bewegen sind F(z) und G(z) die empirischen Verteilungsfunktionen der beiden Grundgesamtheiten (hier: 1te und 2te Klasse).
Da die Hypothese in Worten klar ist, sollte die Übersetzung in Formeln eigentlich nicht alzu schwer sein.
Wir testen: Streuung in der ersten Klasse ist größer als in der 2ten.
Falls die Streuung in beiden Klassen gleich sein würde, gilt F(z)=G(z) oder auch anders geschrieben F(z) = G(1z) <=> F(z) = G(
) für
.
Ist die Streuung hingegen unterschiedlich unterscheiden sich beide Verteilungsfunktionen um den Parameter
, also F(z) = G(
).
Da jetzt danach gefragt ist, ob die Streuung größer ist, unterscheiden sich die beiden Verteilungsfunktionen im Parameter
da für
Gleichheit und für
eine kleinere Streuung vorliegt.
Spontan mit der mir vorliegenden Tabelle für den Wilcoxon Rangsummen Test komme ich auf einen kritischen Wert von 14, da mit
$)
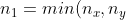und
$)
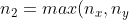hier gilt:
und
Hoffe ich konnte etwas helfen.
Mit freundlichen Grüßen,
M.
Wie kann ich den Sachverhalt nun in Worten ausdrücken? 