STATISTIK-FORUM.de

[waidschrat]

Huhu Holger,

Hmm, weiß nicht, was an meinem Argument "zu einfach" war.

Sorry; das bezog sich lediglich auf dein knappes Kommentar zum Thema Informatonskriterien, denn auch bei konventionellen Fit indizes wird die Modell-Sparsamkeit in Form der Freiheitsgrade mit berücksichtigt. In Gegensatz dazu bewerten BIC, AIC etc. Modelle in Bezug auf ihren prädiktiven Wert.

Jetzt kommt es darauf an, was du mit Modellannahmen meinst. Es gibt eine Menge. Für mich zentral ist die Annahme der korrekten kausalen Spezifikation. Für Statistiker, die einen großen Teil der Literatur in SEM beitragen, ist das oft wenig Interesse, da sie sich lediglich eben mit statistischen Dingen wie Robustheit etc. beschäftigen. Für mich als inhaltlichen Forscher nur soweit von Belang, wie meine theoretische Perspektive bedroht ist.

Ok, sehen wir davon ab, dass die neure Entwicklung von Strukturgleichungsmodelle nicht in erster Linie durch Statistiker, sondern durch praktisch orientierte Methodologen der Sozio- und Psychologie vorangetrieben wurde (Curran, Bentler, McCallum, Bollen, McArdle ua.). Statistiker freuen sich, eher wie du, Holger, über Datenpassung. O.a. Gruppe geht es hingegen aber um die Spezifikation korrekter Kausalmodelle (die wiederrum bestimmte strukturelle Eigenschaften von Daten implizieren -> Modellannahmen). Du schreibst, dass es dir eigentlich auch darum ginge, aber deine Argumentation lässt eher einen anderen Schluss zu.. Wie du schreibst, sind Missspezifikationen nur dann für dich von Belang, wenn sie deine theoretische Perspektive bedrohen würden und genau da liegt der Hase im Pfeffer, denn überkomplexe Modelle tun genau das.
Gehen wir mal davon aus, dass du zwei fittende und sehr komplexe Modelle (mit identischen Freiheitsgraden) konstruierst. Eines ist faktisch (in Bezug auf die Abbildung der „wahren“, datengenerierenden Kausalbeziehungen) falsch spezifiziert, fittet aber sehr gut. Das andere „fittet mit“ Abstand schlechter, wäre aber faktisch korrekt. Wenn du nun diese hochkomplexen Modelle an einer anderen Stichprobe (siehe weiter unten, um Verwechselungen vorzubeugen) validieren möchtest, wäre die Chance relativ groß, dass du bei deinem favorisierten Model einen Missfit bekommst, was einzig und allein an (für den datengenerierenden Prozess) inadäquaten Parametern liegt, die nur deiner ursprünglichen Stichprobe den Fit verbessern. Jetzt gehen wir einen Schritt zurück und denken uns, dass du das 2., richtige, aber in deiner Stichprobe schlecht fittende Modell, gar nicht erst berichtest, weil du es verworfen hast und du es davon abgesehen nicht sinnvoll interpretieren konntest. Stattdessen berichtest du ein weniger komplexes Model als „preliminary“, dass nested in beiden kontrastierten Modellen war. Bei der Replikation wird sich nun zeigen, dass dieses preliminary modell deutlicher weniger fitness verliert, als dein Favorisiertes. Vielleicht fallen auch beide unter die Signifikanzschwelle, mit dem verworfenen wärs dir aber nicht so gegangen. Ich denke, es sollte klar werden, dass die Kausalstruktur dieses „sparsameren“ Modells dichter am Datengenerierenden Prozess ist, als dein missspezifiziertes, aber vermeintlich überlegenes Modell.

Und zur Überprüfung der kausalen Spezifikation ist die Replikation (auch wenn das häufig so gesehen wird), kein Königsweg, sondern relativ wertlos. Eine Replikation mit einer identischen Stichprobe überprüft, ob das Modell stichproben - ideosynkratisch gefittet hat (das hattest du angesprochen) - eine Replikation in einer anderen Stichprobe oder veränderten Bedingungen testet die Generalisierbarkeit.

Sehe ich nicht so, da man bei der adäquaten Interpretation von Parametern immer unterstellt, dass die spezifizierten Modelle valide die Kausalstruktur abbilden. Den Begriff Generalisierbarkeit habe ich bewusst vermieden, da man im deutschen Sprachgebrauch auf die Idee kommen könnte, dass man die externe Validität durch Replikation überprüft. Tatsächlich dient Replikation in der von mir benutzten Bedeutung der Überprüfung der interne Validität, sprich der Gültigkeit der Kausalstruktur gegeben der (Sub-)population für die das Modell Gültigkeit besitzen soll (wohlgemerkt keine ideosynkratisch Testung). Diese ist eine Grundbedingung für die Bewertung von Model-Fit. Ohne die Annahme interner Validität wäre statistische Inferenz in jeglicher Form überflüssig und unnütz.

Ein misspezifiertes aber fittendes Modell wird auch in einer neuen Stichprobe wieder fitten. Wenn du z.B. ein Modell genau so wie du es kritisiert hast, "verschönt" durch absurde Parameter und es so noch misspezifierter wird, und du testest es in einer neuen Stichprobe, wird es wieder fitten.

Falsch (siehe auch oben). Für weitere Erörterung wäre es notwendig, dass du dir die einschlägige Literatur zu Gemüte führst, in der divergente Interpretationen aufgrund konventioneller Fitindizes auch ganz praktisch anhand von Beispielen dokumentiert werden.

Was wenn das korrekte Modell nicht sparsam ist? Dann ist das "weniger komplexe Modell" misspezifiziert. "Zu gut fittend" gibt es m.E. nicht. Allerdings sehe ich es (auch) so, dass *saturierte* Modelle (meinst du das mit komplex?) ein kleineres Falsifikationspotential haben - d.h. ein saturiertes Modell mit gutem fit hat eine geringere Überzeugungskraft, weil die eben Gefahr besteht, dass man mit unsinnigen Parametern, den (sonst sichtbaren) misfit kompensiert. Nur hat das m.E. Implikationen für das Design (--> Modelle so spezifizieren, dass sie Restriktionen beinhalten) - nicht für die post-hoc-Anwendung von BIC & Co. Ich bin z.B. ein großer Fan von Instrumentalvariablen, weil diese genau diese essentiellen Restriktionen bieten.

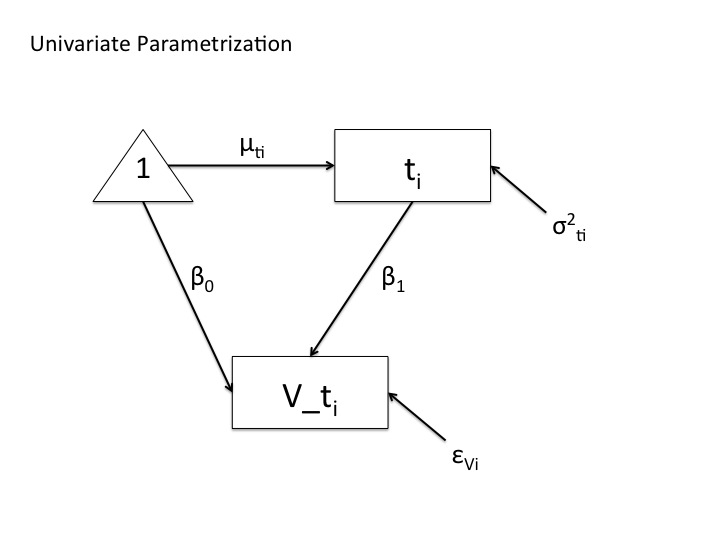
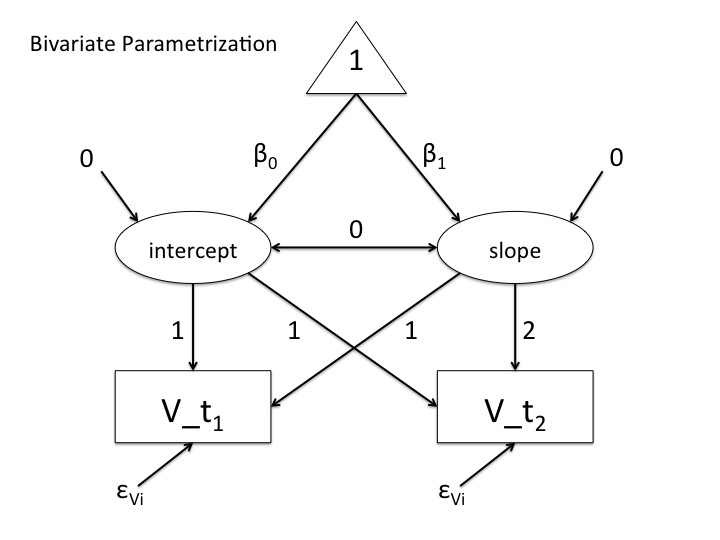
Hab mal 2 Pfaddiagramme fertig gemacht und angehangen – verschiedene Modelle, die identische Parameterschätzungen erzeugen, nur mit dem Unterschied, dass das univariate Modell gesättigt ist, das andere nicht. Wenn man sich das multivariate Modell anschaut stellt man anhand von chisquare basierter Fitindizes fest, dass es die Datenstruktur nicht adäquat replizieren kann, das univariate hingegegen perfekt. Beide Modell haben gleiche logLikelihood und gleiches AIC. BIC ist bei großen Stichproben auch asymptotisch gleich. Fittet das Modell die Daten jetzt erschöpfend oder nicht?

Folie2.jpg (27.21 KiB) 1566-mal betrachtet

Folie1.jpg (42.01 KiB) 1566-mal betrachtet

Interessante Diskussion by the way

Dito

Gruß, R

[Holgonaut]

Hi Robert,

das ist ne Menge Holz, das ich nicht alles kommentieren kann/mag. Daher nur ein paar Anm. Generell sollten wir aber aufpassen, dass wir uns nicht in Ecken drängen, in die wir nicht
gehören. Vielem kann ich durchaus zustimmen. Dass du das als Gegenargument verwendest zeigt, dass ich bei manchem nicht klar genug war.

Ok, sehen wir davon ab, dass die neure Entwicklung von Strukturgleichungsmodelle nicht in erster Linie durch Statistiker, sondern durch praktisch orientierte Methodologen der Sozio- und Psychologie vorangetrieben wurde (Curran, Bentler, McCallum, Bollen, McArdle ua.). Statistiker freuen sich, eher wie du, Holger, über Datenpassung. O.a. Gruppe geht es hingegen aber um die Spezifikation korrekter Kausalmodelle (die wiederrum bestimmte strukturelle Eigenschaften von Daten implizieren -> Modellannahmen). Du schreibst, dass es dir eigentlich auch darum ginge, aber deine Argumentation lässt eher einen anderen Schluss zu..

Du sprichst oft von Fitindizes. Hast das Gefühl, dass ich die verteidige? Nein, das tu ich nicht. Ich bin für eine theoriegeleitete Spezifikation des Modells, und Akzeptieren von Evidenz dagegen. Und Evidenz ist ein sign. Chi-Quadrat-Test, als auch sinnvolle Parameterschätzungen (Stichwort nomologisches Netz). Das heißt, ich "freue" mich nicht für eine simple Datenanpassung, denn die sagt nicht, dass das Modell auch korrekt ist. Viele der von der angegebenen Personen verteidigen allerdings Fitindizes, was zeigt, dass sie schon über eine Datenanpassung freuen und ein bestimmtes Ausmaß von Problemen in einem Modell hinnehmen.

Wie du schreibst, sind Missspezifikationen nur dann für dich von Belang, wenn sie deine theoretische Perspektive bedrohen würden und genau da liegt der Hase im Pfeffer, denn überkomplexe Modelle tun genau das.

Wenn das theoretische Modell nun mal komplex ist, kann ich nichts anderes tun als es zu testen und zu schauen, ob es Belege dagegen gibt. Wenn nein, behalt ich es bei, weiß aber nicht ob es stimmt. Das es falsch sein kann, ist ein allgemeines Problem der Erkenntnisphilosophie (fallacy of affirming the consequent). Und ob das Modell "überkomplex" oder "adäquat komplex" ist, weißt du nicht, weil du das Populationsmodell nicht kennst.

Gehen wir mal davon aus, dass du zwei fittende und sehr komplexe Modelle (mit identischen Freiheitsgraden) konstruierst. Eines ist faktisch (in Bezug auf die Abbildung der „wahren“, datengenerierenden Kausalbeziehungen) falsch spezifiziert, fittet aber sehr gut. Das andere „fittet mit“ Abstand schlechter, wäre aber faktisch korrekt. Wenn du nun diese hochkomplexen Modelle an einer anderen Stichprobe (siehe weiter unten, um Verwechselungen vorzubeugen) validieren möchtest, wäre die Chance relativ groß, dass du bei deinem favorisierten Model einen Missfit bekommst, was einzig und allein an (für den datengenerierenden Prozess) inadäquaten Parametern liegt, die nur deiner ursprünglichen Stichprobe den Fit verbessern.

Genau aus diesen Gründen sind Modellvergleiche problematisch (und damit das Gebot, das Modell mit dem geringeren AIC zu nehmen), weil das besser fittende, aber falsche Modell ausgewählt werden würde.
Ansonsten: Da das zweite Modell korrekt spezifiziert ist, ist es folglich "adäquat komplex". Damit wird der Chi-Quadrat-Test n.s. sein (ignorieren wir mal den alpha-Fehler). Meinst du das mit "meinem favorisierten Modell"? Abgesehen davon: Es wird auch in einer Replikation wieder fitten. Warum auch nicht? Es ist doch korrekt? Das erste - falsche - Modell wird ebenfalls fitten, sei denn, die inadäquaten Parameter sagen Kovarianzen voraus, die NUR FÜR DIESE Stichprobe gelten und durch sampling error hervorgerufen wurden (was du ja meinst mit " was einzig und allein an den [...] inadäquaten Parametern liegt, die nur in deiner ursprünglichen Stichprobe den Fit verbessern"). Das zentrale Problem ist aber nicht diese Stichproben-ideosynkratische Datenanpassung, sondern *systematische* Misspezifikationen durch inadäquate Parameter. Das lässt sich leicht durch eine Simulation zeigen (Abb. siehe unten): Dabei hab ich ein Populationsmodell spezifiziert, dann das Stichprobenmodell vollkommen vermurkst und dann die Parameter mit den höchsten Modifikationsindizes reingenommen. Als Ergebnis bekommst man ein völlig unsinniges Modell, dass aber einen nicht-signifikanten Chi-Quadrat-Test hat. Zieht man 1000 Stichproben, ist die Chi-Quadrat-Statistik exakt Chi-Quadrat-verteilt, wie sie sein sollte. D.h. das Modell fittet in 95% der Fälle.

Jetzt gehen wir einen Schritt zurück und denken uns, dass du das 2., richtige, aber in deiner Stichprobe schlecht fittende Modell, gar nicht erst berichtest, weil du es verworfen hast und du es davon abgesehen nicht sinnvoll interpretieren konntest.

Daher bin ich auch nicht für ein "unter-den-Teppich-kehren" von nicht-fittenden Modellen, sondern für ein theoriegeleitete Re-Spezifizierung.
Den Rest des Absatzes versteh ich allerdings nicht mehr...Das Modell fittet in meiner Stichprobe doch nicht *schlecht*, sondern schlechtER als das erste Modell? Es wird in 5% der Fälle (durch sampling error erwartet) schlecht fitten. Auch das mit dem "nicht sinnvoll" interpretieren versteh ich nicht. Wir verheddern uns glaub ich etwas.

In den nächsten beiden Absätzen verteidigst du weiter die Replikation als Validierung eines gefitteten Modells. Da liegst du, sorry, einfach falsch, was ich oben m.E. gezeigt hab. Nimm als weiteres Beispiel die Klasse der äquivalenten Modelle. Eins davon ist korrekt, zig andere erzeugen exakt den selben Fit, sind aber falsch. Semmelst du nun daneben und spezifizierst eines dieser falschen Modelle, wird es fitten, weil die Konfiguration der Parameter die Kovarianzmatrix adäquat repliziert. Hayduk hat das in SEMNET "capitalization on non-chance" genannt. Ziehst du eine neue Stichprobe und re-spezifzierst du das Modell erneut, fittet es wieder. In 100 Stichproben wird es 95x fitten. Simulier das doch einfach mal, dann siehst du es. Ich hab es mal mit folgendem Modell gemacht: Das Populationsmodell war ein 2 Faktormodell (mit je 2 Indikatoren), Du spezifizierst es fälschlicherweise als ein 1-Faktormodell mit korrelierten Messfehlern. Der Fit ist identisch. Wenn du jetzt weitere Stichproben ziehst, wird dieses falsche-aber-fittende Modell wieder fitten - was du fälschlicherweise als Validierung des 1-Faktormodels interpretierst. Der "Königsweg" ist es also, weitere Restriktionen einzufügen (vielleicht durch andere Variablen, externe Kriterien, Instrumentalvariablen etc.). Fügst du z.B. in dem o.g. Beispiel eine endogene Variable ein, auf die der Pseudo-Faktor einen Effekt hat, fliegt der Schwindel auf - trotz Messfehlerkorrelation.

Deinem abschließenden Beispiel (ich hoffe, ich hab das Beispiel korrekt verstanden) stimm ich zu, seh aber nicht, wo ich was anderes gesagt hätte. Ich hab schon im vorherigen posting gesagt, dass du mit der Menge der Parameter, natürlich einen vorhandenen Misfit auffangen und maskieren kannst. Deshalb ist ein fittendes Modell mit vielen Restriktionen überzeugender, weil es mehr Hürden überwindet, als ein vollgepropftes. Dumm nur, wenn das theoretische Modell nun mal komplex ist. Dann bleibts halt bei "keine Evidenz gegen das Modell". Mehr kann man nicht tun.

Grüße
Holger