Hallo Zusammen!
Ich hab eine theoretische Frage. Warum sollten Fehlerterme nicht korrelieren? Rein aus meiner Logik heraus würde ich es sogar als sinnvoll erachten, wenn Fehlerterme von Indikatoren, die eine latente Variable abbilden signifikant korrelieren.
Vielen Dank für eure Antworten!
Flow
Fehlertermkorrelation
Thema bewerten: 




 • 10 Beiträge
• Seite 1 von 1
• 10 Beiträge
• Seite 1 von 1
- Flow
- Power-User

- Beiträge: 61
- Registriert: Mi 31. Aug 2011, 14:22
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Fehlertermkorrelation
Hi Flow.
dies betrifft die "lokale stochastische Unabhängigkeit" der Indikatoren und ist ein zentrales Merkmal des common factor models. Dies bedeutet, dass der Faktor
die gemeinsame Ursache der Indikatoren ist und dadurch die ihre Kovarianz bedingt und somit aufklären kann.
Fehlerkovarianzen deuten auf eine Verletzung dieser Annahme hin, d.h. zwei oder mehr Indikatoren haben noch eine weitere gemeinsame Ursache oder beeinflussen sich
gegenseitig. Das ist erstens ein Alarmsignal, dass vielleicht das ganze common factor modell misspezifiziert ist (d.h. auch den ersten wesentlichen Faktor gibt es vielleicht so
gar nicht) und dass es einen weiteren Faktor gibt (der die Fehlerkovarianz verursacht), der aber im Modell nicht auftaucht.
Faktoren sind "latente Variablen" -d.h. Phänomene, von denen wir denken, dass sie existieren - die wir aber nicht sehen können. Damit solche Dinge nicht den selben Stellenwert
wie Erdstrahlen und Poltergeister haben, müssen sie eben diesen Annahmen genügen. Das ist das mindeste.
Warum denkst du, dass Fehlerkovarianzen sinnvoll sind?
Grüße
Holger
dies betrifft die "lokale stochastische Unabhängigkeit" der Indikatoren und ist ein zentrales Merkmal des common factor models. Dies bedeutet, dass der Faktor
die gemeinsame Ursache der Indikatoren ist und dadurch die ihre Kovarianz bedingt und somit aufklären kann.
Fehlerkovarianzen deuten auf eine Verletzung dieser Annahme hin, d.h. zwei oder mehr Indikatoren haben noch eine weitere gemeinsame Ursache oder beeinflussen sich
gegenseitig. Das ist erstens ein Alarmsignal, dass vielleicht das ganze common factor modell misspezifiziert ist (d.h. auch den ersten wesentlichen Faktor gibt es vielleicht so
gar nicht) und dass es einen weiteren Faktor gibt (der die Fehlerkovarianz verursacht), der aber im Modell nicht auftaucht.
Faktoren sind "latente Variablen" -d.h. Phänomene, von denen wir denken, dass sie existieren - die wir aber nicht sehen können. Damit solche Dinge nicht den selben Stellenwert
wie Erdstrahlen und Poltergeister haben, müssen sie eben diesen Annahmen genügen. Das ist das mindeste.
Warum denkst du, dass Fehlerkovarianzen sinnvoll sind?
Grüße
Holger
- Holgonaut
- Foren-Unterstützer

- Beiträge: 767
- Registriert: Do 2. Jun 2011, 18:20
- Danke gegeben: 3
- Danke bekommen: 207 mal in 198 Posts
Re: Fehlertermkorrelation
Hallo Holgonaut,
vielen Dank für deine Antwort, die mir sehr weitergeholfen hat!
Der Grund warum ich annahm, dass Fehlerkovarianzen für mich logisch waren ist, dass bestimmte Indikatorvariablen ja das gleich latente Konstrukt abbilden sollten. Der latente Faktor sollte dann wiederum bei allen Indikatorvariablen ähnlich viel an Varianz NICHT aufklären können (was wiederum zu einer signifikanten Fehlerkovarianz führen müsste). Diesbezüglich war dein Beitrag für mein Grundverständnis goldwert.
Viele Grüße
Flow
vielen Dank für deine Antwort, die mir sehr weitergeholfen hat!
Der Grund warum ich annahm, dass Fehlerkovarianzen für mich logisch waren ist, dass bestimmte Indikatorvariablen ja das gleich latente Konstrukt abbilden sollten. Der latente Faktor sollte dann wiederum bei allen Indikatorvariablen ähnlich viel an Varianz NICHT aufklären können (was wiederum zu einer signifikanten Fehlerkovarianz führen müsste). Diesbezüglich war dein Beitrag für mein Grundverständnis goldwert.
Viele Grüße
Flow
- Flow
- Power-User

- Beiträge: 61
- Registriert: Mi 31. Aug 2011, 14:22
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Fehlertermkorrelation
Hi,
du hast einen Denkfehler:
Erstens: Die nicht aufgeklärte Varianz umfasst alle ausgeschlossenen Ursachen (außer der latenten Variable) - d.h. systematische und zufällige Messfehler. Das die latente Variable überall gleich viel Varianz NICHT erklärt ist ein Sonderfall eines Messinstruments - nämlich die parallele Messung - muss aber nicht zwangsläufig so sein. Es können ja verschiedene Items durchaus von unterschiedlich starken weiteren Ursachen betroffen sein. Als Folge hat ein item eine starke Messfehlervarianz, dass andere eine geringe. Bsp. "ich bin zufrieden mit meiner Arbeit" und "ich würde meinen job jederzeit wieder wählen". Beide (nehmen wir mal an) messen die latente Variable Arbeitszufriedenheit - aber das erstere ist viel einfacher und intuitiver (geringer Messfehler) als das zweite (hoher Messfehler).
Zweitens: Selbst wenn der Anteil der Varianz, die nicht durch die latente Variablen erklärt ist, gleich ist, folgt daraus keine Korrelation. Erinnere dich: Eine Fehlerkorrelation ist eine partielle Korrelation (die Korrelation der items, wenn die gemeinsame latente Variable auspartialisiert wurde). Der Rest sollte nicht korrelieren, weil die Restvarianz zwei unabhängige Zufallsvariablen sind - es sei denn, sie haben weitere *gemeinsame* Ursachen (z.B. ein bestimmtes wording in der item-Formulierung).
Grüße
Holger
du hast einen Denkfehler:
.Der latente Faktor sollte dann wiederum bei allen Indikatorvariablen ähnlich viel an Varianz NICHT aufklären können (was wiederum zu einer signifikanten Fehlerkovarianz führen müsste)
Erstens: Die nicht aufgeklärte Varianz umfasst alle ausgeschlossenen Ursachen (außer der latenten Variable) - d.h. systematische und zufällige Messfehler. Das die latente Variable überall gleich viel Varianz NICHT erklärt ist ein Sonderfall eines Messinstruments - nämlich die parallele Messung - muss aber nicht zwangsläufig so sein. Es können ja verschiedene Items durchaus von unterschiedlich starken weiteren Ursachen betroffen sein. Als Folge hat ein item eine starke Messfehlervarianz, dass andere eine geringe. Bsp. "ich bin zufrieden mit meiner Arbeit" und "ich würde meinen job jederzeit wieder wählen". Beide (nehmen wir mal an) messen die latente Variable Arbeitszufriedenheit - aber das erstere ist viel einfacher und intuitiver (geringer Messfehler) als das zweite (hoher Messfehler).
Zweitens: Selbst wenn der Anteil der Varianz, die nicht durch die latente Variablen erklärt ist, gleich ist, folgt daraus keine Korrelation. Erinnere dich: Eine Fehlerkorrelation ist eine partielle Korrelation (die Korrelation der items, wenn die gemeinsame latente Variable auspartialisiert wurde). Der Rest sollte nicht korrelieren, weil die Restvarianz zwei unabhängige Zufallsvariablen sind - es sei denn, sie haben weitere *gemeinsame* Ursachen (z.B. ein bestimmtes wording in der item-Formulierung).
Grüße
Holger
- Holgonaut
- Foren-Unterstützer

- Beiträge: 767
- Registriert: Do 2. Jun 2011, 18:20
- Danke gegeben: 3
- Danke bekommen: 207 mal in 198 Posts
Re: Fehlertermkorrelation
Vielen Dank Holger für die Denkfehlerkorrektur!
Leider sind mir im Zuge dessen zwei weitere Fragen in den Sinn gekommen:
(1) Sind Fehlerkovarianzen dann bei Messwiederholung erlaubt? Ich messe ein latentes Konstrukt z.B. IQ an zwei verschiedenen Messzeitpunkten. Wenn der IQ Test reliabel ist sollten die Fehlerterme doch korrelieren?
(2) Was ist der Unterschied zwischen Residualvarianz und Fehlervarianz? Für mich ist es das gleiche. In den Lehrbüchern steht , dass nur über die latente Variablenkonstruktion der Messfehler explizit berücksichtigt wird, während bei manifester Variablenbeobachtung das nicht geschieht. Trotzdem finde ich die Residualvarianz im Output und auch in der Regressionsgleichung.
Viele Grüße
Flow
Leider sind mir im Zuge dessen zwei weitere Fragen in den Sinn gekommen:
(1) Sind Fehlerkovarianzen dann bei Messwiederholung erlaubt? Ich messe ein latentes Konstrukt z.B. IQ an zwei verschiedenen Messzeitpunkten. Wenn der IQ Test reliabel ist sollten die Fehlerterme doch korrelieren?
(2) Was ist der Unterschied zwischen Residualvarianz und Fehlervarianz? Für mich ist es das gleiche. In den Lehrbüchern steht , dass nur über die latente Variablenkonstruktion der Messfehler explizit berücksichtigt wird, während bei manifester Variablenbeobachtung das nicht geschieht. Trotzdem finde ich die Residualvarianz im Output und auch in der Regressionsgleichung.
Viele Grüße
Flow
- Flow
- Power-User

- Beiträge: 61
- Registriert: Mi 31. Aug 2011, 14:22
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Fehlertermkorrelation
Hi Flow
zu 1) Ja. Wie ich schrieb, enthält jede Fehlervarianz systematische Messfehler. Wenn du ein item zu zwei verschiedenen Zeitpunkten als Messungen einer latenten Variable modellierst, korrelieren die systematischen Anteile über die Zeit. Das ist erwartbar und sollte eingefügt werden. Außerdem: Es ist nicht so, dass Messfehlerkorrelationen nicht "erlaubt" sind. Wenn du dir deine items anschaust, und siehst, dass z.B. zwei einen gleichen item-Stamm haben (was sie vom dritten oder vierten item im Messmodell abgrenzt), ist es zu erwarten, dass deren Messfehler korrelieren.
zu 2) Strengenommen hat der Begriff "Residuum" in SEM nichts verloren. Es ist ein Begriff aus der Regressionsanalyse, der ganz simple die Abweichung der Daten von der Regressionsgerade angibt. Ein Fehlerterm (in Regression oder SEM) ist ein theoretisches Konzept, dass angibt, wie groß der Bereich ausgeschlossener weiterer Ursachen auf die entsprechende abhängige Variable ist. Fehlerterme haben sowohl abhängige beobachtete Variablen (Indikatoren) als auch abhängige latente Variablen. Die Messmodell-Modellierung und damit die Modellierung der MESSfehler der Indikatoren ist v.a. bei unabhängigen latenten Variablen von Vorteil, weil der Messfehler sonst dazu führt, dass die Effekte der latenten Variablen verzerrt werden (Endogenität). Bei der abhängigen Variablen passiert das nicht.
Grüße
Holger
zu 1) Ja. Wie ich schrieb, enthält jede Fehlervarianz systematische Messfehler. Wenn du ein item zu zwei verschiedenen Zeitpunkten als Messungen einer latenten Variable modellierst, korrelieren die systematischen Anteile über die Zeit. Das ist erwartbar und sollte eingefügt werden. Außerdem: Es ist nicht so, dass Messfehlerkorrelationen nicht "erlaubt" sind. Wenn du dir deine items anschaust, und siehst, dass z.B. zwei einen gleichen item-Stamm haben (was sie vom dritten oder vierten item im Messmodell abgrenzt), ist es zu erwarten, dass deren Messfehler korrelieren.
zu 2) Strengenommen hat der Begriff "Residuum" in SEM nichts verloren. Es ist ein Begriff aus der Regressionsanalyse, der ganz simple die Abweichung der Daten von der Regressionsgerade angibt. Ein Fehlerterm (in Regression oder SEM) ist ein theoretisches Konzept, dass angibt, wie groß der Bereich ausgeschlossener weiterer Ursachen auf die entsprechende abhängige Variable ist. Fehlerterme haben sowohl abhängige beobachtete Variablen (Indikatoren) als auch abhängige latente Variablen. Die Messmodell-Modellierung und damit die Modellierung der MESSfehler der Indikatoren ist v.a. bei unabhängigen latenten Variablen von Vorteil, weil der Messfehler sonst dazu führt, dass die Effekte der latenten Variablen verzerrt werden (Endogenität). Bei der abhängigen Variablen passiert das nicht.
Grüße
Holger
- Holgonaut
- Foren-Unterstützer

- Beiträge: 767
- Registriert: Do 2. Jun 2011, 18:20
- Danke gegeben: 3
- Danke bekommen: 207 mal in 198 Posts
Re: Fehlertermkorrelation
Vielen Dank für die Antwort! Zunehmend wird mir einiges klarer!
Aber wie sieht es aus, wenn ich Probanden habe die z.B. zu 4 Messzeitpunkten immer das gleiche lernen mussten und ich mir nun die Veränderung über die Zeit ansehe. Ich gehe ja davon aus, dass sie mit jedem Testzeitpunkt höhere Leistungscores erhalten. Soll ich hier eine Fehlerkovarianz annehmen? Es wird ja schlussendlich immer das gleiche gelernt. Oder nicht? Weil ich ja einen Lernzuwachs annehme?
Viele Grüße
Flow
Aber wie sieht es aus, wenn ich Probanden habe die z.B. zu 4 Messzeitpunkten immer das gleiche lernen mussten und ich mir nun die Veränderung über die Zeit ansehe. Ich gehe ja davon aus, dass sie mit jedem Testzeitpunkt höhere Leistungscores erhalten. Soll ich hier eine Fehlerkovarianz annehmen? Es wird ja schlussendlich immer das gleiche gelernt. Oder nicht? Weil ich ja einen Lernzuwachs annehme?
Viele Grüße
Flow
- Flow
- Power-User

- Beiträge: 61
- Registriert: Mi 31. Aug 2011, 14:22
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Fehlertermkorrelation
Hi Flow,
das kann ich schlecht beurteilen. Kannst ja mal mehr zur Messung und relevanten latenten Variable schreiben. Dabei stellt sich mir zunächst die Frage, ob das überhaupt ein Faktormodell ist. Denk dran, dass Faktormodell sagt, dass eine
singuläre/spezifische/eindimensionale Entität durch mehrere Indikatoren reflektiert wird. Lernergebnisse sind oft multidimensional.
Grundsätzlich zum Thema "Veränderung über die Zeit": Die würde man Veränderung der *latenten* Mittelwerte über die Zeit erfassen - Messfehlerkorrelationen sollte es dennoch geben, wenn die selben Indikatoren benutzt werden. Dies ist
eine Voraussetzung, damit man überhaupt von der Identität der latenten Variable ausgehen kann (sogar Gleichheit der Ladungen).
Golembiewski, R. T., Billingsley, K., & Yeager, S. (1976). Measuring change and persistence in human affairs: Types of change generated by OD designs. Journal of Applied Behavioral Science, 12, 133-157.
Millsap, R. E., & Hartog, S. B. (1988). Alpha, beta, and gamma change in evaluation research. Journal of Applied Psychology, 73, 564-574.
Schaubroeck, J., & Green, S. G. (1989). Confirmatory factor analytic procedures for assessing change during organizational entry. Journal of Applied Psychology, 74, 892-900.
Pentz, M. A., & Chou, C.-P. (1994). Measurement invariance in longitudinal research assuming change from development and intervention. Journal of Consulting and Clinical Psychology, 62, 450-462.
Vandenberg, R. J., & Self, R. M. (1993). Assessing newcomers´ changing commitments to the organization during the first 6 months of work. Journal of Applied Psychology, 78(4), 557-568.
Grüße
Holger
das kann ich schlecht beurteilen. Kannst ja mal mehr zur Messung und relevanten latenten Variable schreiben. Dabei stellt sich mir zunächst die Frage, ob das überhaupt ein Faktormodell ist. Denk dran, dass Faktormodell sagt, dass eine
singuläre/spezifische/eindimensionale Entität durch mehrere Indikatoren reflektiert wird. Lernergebnisse sind oft multidimensional.
Grundsätzlich zum Thema "Veränderung über die Zeit": Die würde man Veränderung der *latenten* Mittelwerte über die Zeit erfassen - Messfehlerkorrelationen sollte es dennoch geben, wenn die selben Indikatoren benutzt werden. Dies ist
eine Voraussetzung, damit man überhaupt von der Identität der latenten Variable ausgehen kann (sogar Gleichheit der Ladungen).
Golembiewski, R. T., Billingsley, K., & Yeager, S. (1976). Measuring change and persistence in human affairs: Types of change generated by OD designs. Journal of Applied Behavioral Science, 12, 133-157.
Millsap, R. E., & Hartog, S. B. (1988). Alpha, beta, and gamma change in evaluation research. Journal of Applied Psychology, 73, 564-574.
Schaubroeck, J., & Green, S. G. (1989). Confirmatory factor analytic procedures for assessing change during organizational entry. Journal of Applied Psychology, 74, 892-900.
Pentz, M. A., & Chou, C.-P. (1994). Measurement invariance in longitudinal research assuming change from development and intervention. Journal of Consulting and Clinical Psychology, 62, 450-462.
Vandenberg, R. J., & Self, R. M. (1993). Assessing newcomers´ changing commitments to the organization during the first 6 months of work. Journal of Applied Psychology, 78(4), 557-568.
Grüße
Holger
- Holgonaut
- Foren-Unterstützer

- Beiträge: 767
- Registriert: Do 2. Jun 2011, 18:20
- Danke gegeben: 3
- Danke bekommen: 207 mal in 198 Posts
Re: Fehlertermkorrelation
Hi Holger,
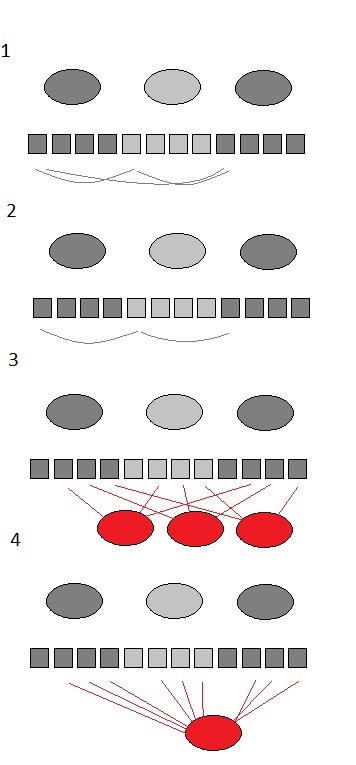
In meinem Beispiel bin ich auf die Indikatorebene gerutscht. Wie du sagst, mein Beispiel bildet kein Faktorenmodell ab. Ich hätte es sollen anders beschreiben. Besser wäre, wenn man davon ausgeht, dass man pro Untersuchungszeitpunkt (von 3) vier Arbeitsgedächtnistests (numerisch, verbal, visual, spatial) mit dem Probanden durchführt. Hier könnte ich nun 3 latente Arbeitsgedächtnisfaktoren bilden und alle Fehlerterme korrelieren lassen. Die Frage, die sich mir hier stellt ist, ob ich alle Fehlerterme korrelieren lassen muss (Abb 1) oder nur die benachbarten (Abb 2). Geiser (2010) hat vorgeschlagen (auf Basis von Eid, Schneider & Schwenkmezger, 1999), dass man überhaupt einen indikatorspezifischen Residualfaktor bilden soll (um den Nachteil der Unterschätzung der Reliabilitäten von Indikatoren zu vermeiden). Hier wird ein Indikator als Referenzindikator ausgewählt (eine Markiervariable, die das zu messende Konstrukt besonders gut repräsentiert). Der Residualfktor repräsentiert den Teil der reliablen Varianz in den Nicht-Referenzindikatoren. Die Frage die sich mir hier stellt ist, ob man nun 3 latente Residualfaktoren bilden muss oder einen (Abb 3 und 4)? Ich gehe mal davon aus, dass es 3 sind. Aber ich will mich doch absichern.
Vielen Dank nochmal für deine Hilfe!
Flow
In meinem Beispiel bin ich auf die Indikatorebene gerutscht. Wie du sagst, mein Beispiel bildet kein Faktorenmodell ab. Ich hätte es sollen anders beschreiben. Besser wäre, wenn man davon ausgeht, dass man pro Untersuchungszeitpunkt (von 3) vier Arbeitsgedächtnistests (numerisch, verbal, visual, spatial) mit dem Probanden durchführt. Hier könnte ich nun 3 latente Arbeitsgedächtnisfaktoren bilden und alle Fehlerterme korrelieren lassen. Die Frage, die sich mir hier stellt ist, ob ich alle Fehlerterme korrelieren lassen muss (Abb 1) oder nur die benachbarten (Abb 2). Geiser (2010) hat vorgeschlagen (auf Basis von Eid, Schneider & Schwenkmezger, 1999), dass man überhaupt einen indikatorspezifischen Residualfaktor bilden soll (um den Nachteil der Unterschätzung der Reliabilitäten von Indikatoren zu vermeiden). Hier wird ein Indikator als Referenzindikator ausgewählt (eine Markiervariable, die das zu messende Konstrukt besonders gut repräsentiert). Der Residualfktor repräsentiert den Teil der reliablen Varianz in den Nicht-Referenzindikatoren. Die Frage die sich mir hier stellt ist, ob man nun 3 latente Residualfaktoren bilden muss oder einen (Abb 3 und 4)? Ich gehe mal davon aus, dass es 3 sind. Aber ich will mich doch absichern.
Vielen Dank nochmal für deine Hilfe!
Flow
- Dateianhänge
-
- Grafik_Statistik Forum.jpg (50.14 KiB) 4767-mal betrachtet
- Flow
- Power-User

- Beiträge: 61
- Registriert: Mi 31. Aug 2011, 14:22
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Fehlertermkorrelation
Moin,
Du kannst diese Faktoren zwar "bilden", aber ob das Modell die Realität beschreibt, musst du noch sehen. Faktorenmodelle sind kausale Modelle, die eine Aussage über die Realtität machen. Diese ist oft falsch.
Dein Modell würde aussagen, dass es einen Faktore "Arbeitsgedächtnis" gibt, der die Leistung in vier unterschiedlichen Tests verursacht. Du bist der Experte und musst überlegen, ob das theoretisch sinnvoll ist.
Der chi-Quadrat-Test sagts dir
Und ja (ich wiederhol mich zum drittenmal): Die Fehler der einzelnen Tests würden über die Zeit kovariieren und zwar alle ("banded error structure", http://dare.uva.nl/document/100222)
Das mit den Residualfaktoren versteh ich nicht (ist noch zu früh Das klingt für mich wie die Modellierung eines Common method factors. Ich meine mich zu erinnern, das Eid et al. das vorschlagen, wenn man verschiedene Methoden hat, die verschiedene Dinge messen (multi-trait-multi-method- Modell). Ich würde da keine Arbeit/Zeit reinstecken. Korrelierende Fehler sind Usus.
Das klingt für mich wie die Modellierung eines Common method factors. Ich meine mich zu erinnern, das Eid et al. das vorschlagen, wenn man verschiedene Methoden hat, die verschiedene Dinge messen (multi-trait-multi-method- Modell). Ich würde da keine Arbeit/Zeit reinstecken. Korrelierende Fehler sind Usus.
Grüße
Holger
Hier könnte ich nun 3 latente Arbeitsgedächtnisfaktoren bilden und alle Fehlerterme korrelieren lassen
Du kannst diese Faktoren zwar "bilden", aber ob das Modell die Realität beschreibt, musst du noch sehen. Faktorenmodelle sind kausale Modelle, die eine Aussage über die Realtität machen. Diese ist oft falsch.
Dein Modell würde aussagen, dass es einen Faktore "Arbeitsgedächtnis" gibt, der die Leistung in vier unterschiedlichen Tests verursacht. Du bist der Experte und musst überlegen, ob das theoretisch sinnvoll ist.
Der chi-Quadrat-Test sagts dir
Und ja (ich wiederhol mich zum drittenmal): Die Fehler der einzelnen Tests würden über die Zeit kovariieren und zwar alle ("banded error structure", http://dare.uva.nl/document/100222)
Das mit den Residualfaktoren versteh ich nicht (ist noch zu früh
Grüße
Holger
- Holgonaut
- Foren-Unterstützer

- Beiträge: 767
- Registriert: Do 2. Jun 2011, 18:20
- Danke gegeben: 3
- Danke bekommen: 207 mal in 198 Posts
Thema bewerten: 




 • 10 Beiträge
• Seite 1 von 1
• 10 Beiträge
• Seite 1 von 1
Zurück zu Pfadanalyse, Strukturgleichungsmodelle & CFA
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 0 Gäste