STATISTIK-FORUM.de

[Flow]

Hallo Zusammen,

mir ist nicht klar was mit dem e bei der Regression passiert. Wird das e in der einfachen (und multiplen) Regressionsformel (y = a +b*x + e) auf 1 oder auf 0 gestellt? Viele Lehrbücher führen zwar einmal das e an, wird aber später nicht mehr berücksichtigt.

Vielen Dank und Grüße
Flow

[daniel]

Zunächst muss zwischen dem theoretischen Fehler (meist , kann aber auch e sein) und den empirischen Residuen (meist e oder ) unterschieden werden.

Die empirischen Residuen sind schlicht die (tatsächlich berechenbaren) Abweichungen der vorhergesagten Werten von den beobachteten Werten.

Für die theoretischen Fehler wird eine (Normal)Verteilung mit Mittelwert 0 und Varianz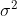 angenommen. Sind diese Annahmen verletzt, kommt es zu Verzerrungen bei der Schätzung der Koeffizienten und/oder Standardfehler.

Interessenat wird das bei der "soziologischen" Herleitung (oder der "light" Variante der Herleitung) des binär logisitischen Modells (etwa hier: http://www.uni-bamberg.de/fileadmin/uni ... g-BBES.pdf). Dort verschwindet der Fehler nämlich in der Tat auf wundersame Art und Weise (die mir auch noch niemand plausibel erklären konnte) und es ist de facto unmöglich das (eigentlich identische) probit Modell auf diese Weise herzuleiten.

Du stellst hier eine wichtige Frage. Versuch die Antwort zu verinnerlichen, und merk Dir einfach schon mal vorab, dass die Annahmen über den Fehler den Hauptunterschied zwischen vielen Regressionsmodellen ausmacht.