STATISTIK-FORUM.de

[burcu]

Hallo, mein hoffentlich letzte Frage vor der Abgabe:

Also, ich habe mehrere Hypothesen hinsichtlich der Beziehung zwischen mehreren (intervall-skalierten) Variablenpaaren (eine abhängige und eine unabhängige) (Wenn Merkmal A hoch, dann ist Merkmal B hoch). Ich habe zur Überprüfung der Beziehung immer jeweils eine Regressionsanalyse berechnet, doch die Werte sind alle eher schlecht (R²).

Nun leuchtet mir etwas spät ein, dass es ja keine VOLLSTÄNDIGEN Erklärungsmodelle sind und die Beziehung zwischen AV und UV auch von anderen Größen abhängt, die in der Regressionsanalyse nicht berücksichtigt wurden. Wäre es dann nicht besser einfach Korrelationen zu berechnen und und zu sagen ja, es existiert ein hoher positiver/negativer oder eben geringer Zusammenhang zwischen AV und UV?

UND, jetzt der eigentlich wichtige Teil meiner Frage: Bei einer Regressionsanalyse sehe ich ja, welche Variable die andere bedingt, welche also die abhänge und welche die unabhängige ist. Doch gibt es Möglichkeit bei Berechnung der Korrelation dies aus zu berücksichtigen?


BITTE um GANZ DRINGENDE ANTWORT!

[statistikwas]

Hallo,
vollständige Varianzaufklärung scheint in meinen Augen eher Utopie zu sein. Daher ist es üblich, dass in Regressionsanalysen die abhängige Variable (Kriterium) nicht durch alle berücksichtigten möglichen UVs (Prädiktoren) völlig aufgeklärt werden kann. Du kannst höchstens sagen, zu welchem Anteil (siehe Rquadrat) das Kriterium mit den anderen aufgenommenen Variablen in Beziehung steht. Es wird in der Statistik immer auch Einflussgrößen geben, die nicht berücksichtigt werden (können).
Der Vorteil von Regressionsanalysen im Vergleich zu Korrelationen liegt darin, dass Regressionen eben andere Größen (wie etwa Störvariablen) berücksichtigen und du daher auf diese kontrollieren kannst - was meines Erachtens eine genauere Abbildung der Wirklichkeit liefert. Denn Regressionen ermöglichen dir ganze Wirkgefüge zu betrachten, anstelle von zwei Variablen alleine.

Eine Korrelation ist, wie auch die Regression eine Berechnung von Zusammenhängen! Obwohl das theoretische Konstrukt der Regression eine Wirkrichtung (Prädiktoren auf Kriterium) annehmen, darf dies dennoch nicht kausal interpretiert werden. Kausalinterpretationen sind in beiden Fällen (bei Korrelation und auch Regression) nicht möglich! Alles was du bei signifikanten bivariaten Korrelationen sagen kannst ist: Es gibt einen Zusammenhang in der Höhe von r zwischen beiden Variablen. Bei der Regression kannst du sagen (sofern das Gesamt-Modell signifikant wurde): Es gibt einen Zusammenhang der Variablen (Prädiktoren) X, Y, Z... und dem Kriterium. Zusätzlich kannst du dir bei Regressionen die Gewichte der einzelnen Variablen (beta-Gewichte) zur Festlegung der Signifikanz und Stärke des Zusammenhangs einzelner Prädiktoren mit dem Kriterium ansehen.

Ich hoffe, ich konnte helfen,
lg, C.

[Druss]

Hallo,

generell gilt, wie bereits dargestellt wurde, Korrelation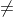 Kausalität. Bestes Negativbeispiel (Scheinkorrelation).

Beim (korrekt spezifiziertem) Regressionsmodell versucht man eine Antwort auf Fragestellungen mit Kausalitätsbezug zu finden. Deshalb unterstellt man hier stets die ceteris paribus Annahme. Man sollte jedoch stets bedenken, dass die Annahme an das korrekt spezifizierte Modell und der c.p. Effekt getroffen werden um die Parameter interpretieren zu können.

Angenommen Du hättest ein Modell mit einem , so liegt die Vermutung nahe, dass es einen deterministischen Zusammenhang zwischen abhängiger und unabhängigen Variablen gibt. Oft ist dies nicht das, was Du in Fragestellungen, in welcher Du Regressionsanalyse betreibst, haben willst. Falls dem doch so ist, beispielsweise, wenn Du die gesamte Populations betrachten kannst/hast, so brauchst Du auch generell keine Annahmen mehr treffen, da Du die Realität, welche Du beschreiben willst, ja kennst.


LG