Hi zusammen,
ich bräuchte dringend eure Hilfe. Ich schreibe grade meine Masterthesis und muss im Rahmen dieser ein Strukturgleichungsmodell durchführen. Leider habe ich niemanden, der sich mit AMOS auskennt, geschweige denn mein Lehrstuhl. Deswegen suche ich bei euch Rat.
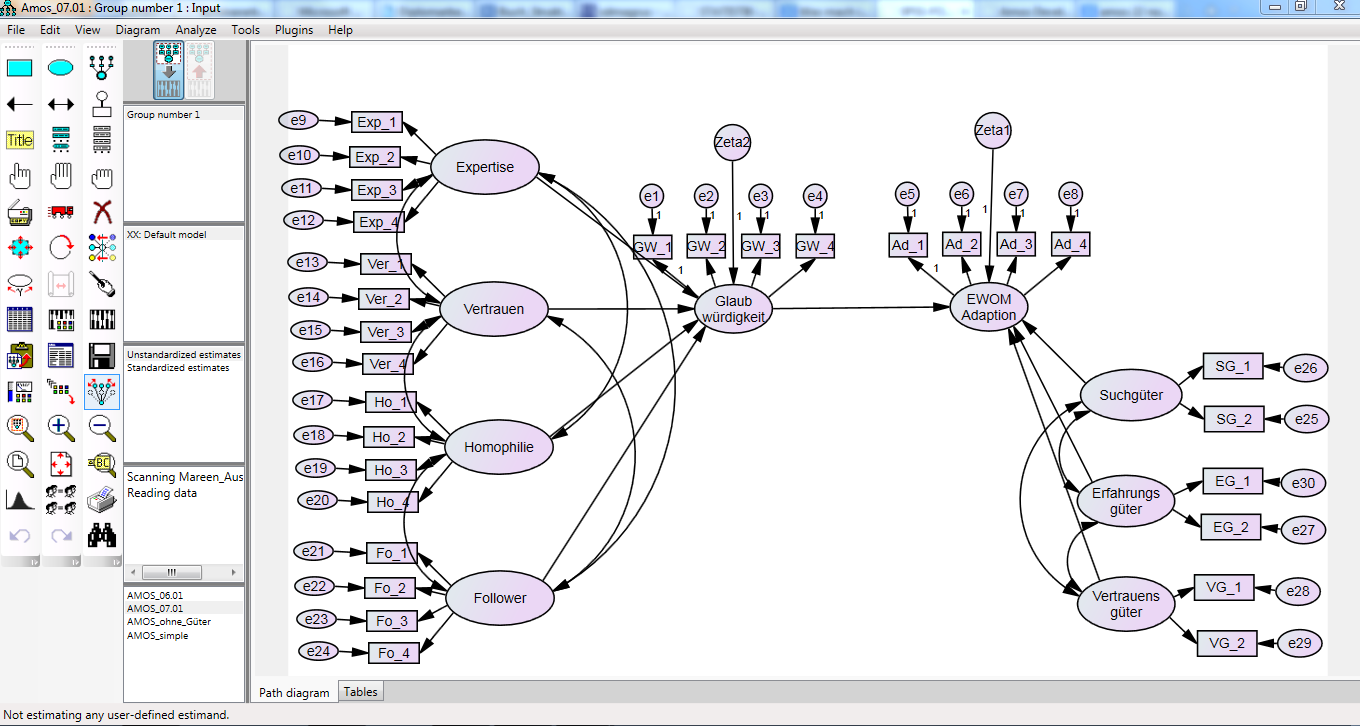
Ich habe mein Pfaddiagramm bei AMOS mit meinem in SPSS gespeichertem Datensatz erstellt. Leider komm ich hier nicht mehr weiter. Ich habe m.M.n. alles genau so gamcht, wie erklärt, aber sobald ich auf Kalkulation klicke, passiert einfach nix. hat da jemand nen Plan? Es kommt noch nicht einmal eine Fehlermeldung. Das einzige, was m.M.n. komisch aussieht, ist, dass unten links in der Status bar steht: not estimating any user defined estimed!
Ist das der Fehler oder habt ihr irgendnen anderen Tipp für mich, warum das nicht läuft?
Ich bin echt so langsam mit meinem Latein am Ende und freue mich sehr über jede kleinste Hilfe.
Liebe Grüße,
Mareen
keine Kalkulation bei AMOS möglich
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
keine Kalkulation bei AMOS möglich
- Dateianhänge
-
- Screenshot_AMOS.PNG (252.07 KiB) 2399-mal betrachtet
- Mary_study
- Grünschnabel

- Beiträge: 2
- Registriert: Do 2. Jan 2014, 14:03
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: keine Kalkulation bei AMOS möglich
Ich glaube du hast bei vielen Messmodellen noch nicht einen der Parameter auf 1 fixiert wodurch die latenten Variablen keine Metrik zugeordnet bekommen. Bei "Glaubwürdigkeit" und "Adaption" in der Mitte hast du das ja gemacht.
Also bei "Expertise" z.B. den Pfad nach Exp_1 anklicken und bei Regression Weight ne 1 eingeben.
Also bei "Expertise" z.B. den Pfad nach Exp_1 anklicken und bei Regression Weight ne 1 eingeben.
- Semson
- Power-User

- Beiträge: 80
- Registriert: Mi 27. Nov 2013, 11:22
- Danke gegeben: 2
- Danke bekommen: 15 mal in 15 Posts
Re: keine Kalkulation bei AMOS möglich
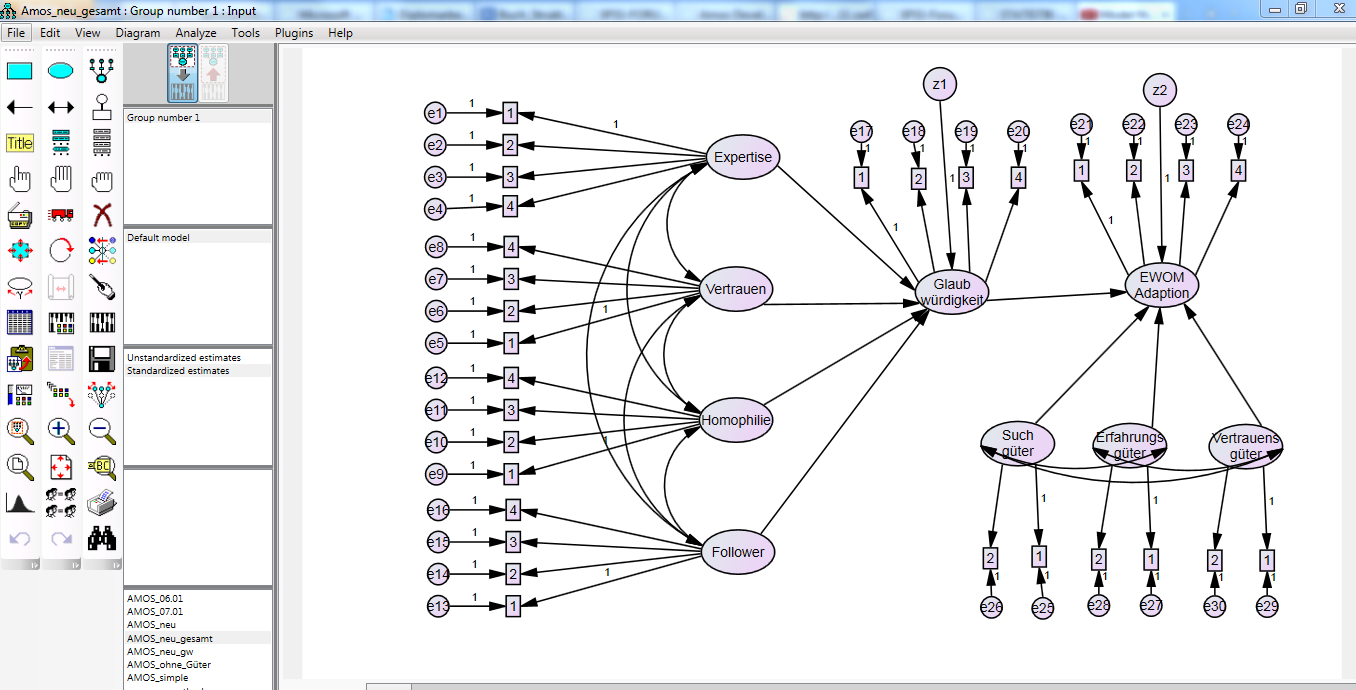
Das hat tatsächlich geklappt  Zumindest die Determinanten und die Glaubwürdigkeit und die EWOM Adaption klappt jetzt. hatte da ein fehler drin... Danke Dir.
Zumindest die Determinanten und die Glaubwürdigkeit und die EWOM Adaption klappt jetzt. hatte da ein fehler drin... Danke Dir.
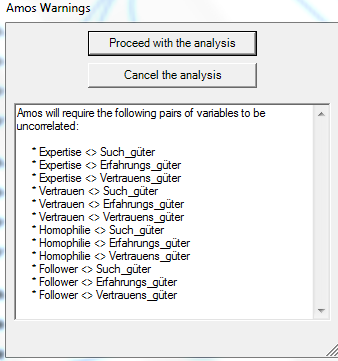
Aber wenn ich jetzt die Güter mit rein nehme, dann poppt folgende Fehlermeldung auf:
Aber wenn ich jetzt die Güter mit rein nehme, dann poppt folgende Fehlermeldung auf:
- Dateianhänge
-
- Screenshot_AMOS_2.PNG (232.78 KiB) 2390-mal betrachtet
- Mary_study
- Grünschnabel

- Beiträge: 2
- Registriert: Do 2. Jan 2014, 14:03
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: keine Kalkulation bei AMOS möglich
Das ist keine Fehlermeldung, sondern vielmehr ein Warnhinweis, dass du eben keine Kovarianzen zwischen diesen exogenen latenten Variablen eingezeichnet hast. Wenn das Modell ausreichend identifiziert ist, müsste es eigentlich laufen wenn du auf "proceed" klickst.
Welche Pfade/Kovarianzen sinnvoll sind und welche nicht ist ne Frage der theoretischen Annahmen, schätze ich. Da müssen wohl die Profis hier ran. Ich kenne das so, dass man exogene latente Variablen meistens korreliert.
Welche Pfade/Kovarianzen sinnvoll sind und welche nicht ist ne Frage der theoretischen Annahmen, schätze ich. Da müssen wohl die Profis hier ran. Ich kenne das so, dass man exogene latente Variablen meistens korreliert.
- Semson
- Power-User

- Beiträge: 80
- Registriert: Mi 27. Nov 2013, 11:22
- Danke gegeben: 2
- Danke bekommen: 15 mal in 15 Posts
Re: keine Kalkulation bei AMOS möglich
Genau. Du hast ja in deinem Modell 6 exogene Variablen.
Normalerweise sind diese miteinander in AMOS korreliert.
Wenn Du aber der Meinung bist, dass es so okay ist, kannst Du auch einfach fortfahren.
Normalerweise sind diese miteinander in AMOS korreliert.
Wenn Du aber der Meinung bist, dass es so okay ist, kannst Du auch einfach fortfahren.
- Albrecht
- Veteran

- Beiträge: 273
- Registriert: Di 26. Nov 2013, 13:04
- Danke gegeben: 32
- Danke bekommen: 54 mal in 54 Posts
Re: keine Kalkulation bei AMOS möglich
Hi,
ich möchte mich meinen Vorschreibern anschließen.
Wichtig bei einem SEM ist, dass du dir der impliziten Annahmen/Restriktionen klar wirst, die du unbewusst oder bewusst ausdrückst:
a) Die beiden Sets von exogenen Variablen korrelieren nicht. Kannst du das wirklich annehmen? Ich halte das für gewagt und der Modellfit wird dir das zeigen.
Generell. Überleg dir ob diese Annahme für das, was du eigentlich ja testen willst, zentral ist. Manche Annahmen sind für die kausale Evidenz des zentralen Anliegens
wichtig / hilfreich, manche unsinnig. Die machen einem das Leben unnötig schwer
b) Die Messmodelle: Ein Messmodell unterstellt, dass die Kovarianzen der Indikatoren durch eine gemeinsame Ursache (die latente Variable) verursacht wurde. Außerdem
unterstellt es, dass die Kovarianzen zwischen den indikatoren der einen Variable und denen der anderen über die Kovarianzen / Effekte dieser latenten Variable laufen.
Sog. d-separation-Implikationen sind: Die Kovarianzen zwischen den Indikatoren einer Variable werden n.s., wenn du die latente Variable konstant hälst. Und die Kovarianzen
zwischen mit den Indikatoren der einen mit denen der anderen Variable werden n.s. wenn du eine der beiden Variablen konstant hälst. Harte Annahmen, die selten funktionieren,
weil der Teufel bei der item-formulierung im Detail liegt. Mit der Variation der Begrifflichkeit in den items hat man schnell eine andere latente Variable gemessen...
Schau dir daher die item-Formulierungen an und überlege, ob es wirklich Sinn macht, dass all diese items eine und dieselbe Variable messen. Denk daran, dass eine Variable eine
maximal spezifische Sache ist!
c) Die Effekte der linken exogenen Variablen auf EWOM sind auf 0 fixiert. Damit unterstellst du nicht nur, dass diese Variablen keinen Effekt haben, sondern auch, dass die empirischen Kovarianzen
zwischen diesen Variablen über ihre Verbindung über Glaubwürdigkeit laufen. Hälst du G.w. konsant, sinken sie auf 0. Das ist eine kausal wichtige Restriktion.
d) die Fehlerkovarianz zwischen G.w. und EWOM ist auf 0 fixiert. Damit unterstellst du dass es keine außerhalb des Modells befindlichen gemeinsamen Ursachen gibt. Wenn das Modell so fittet (d.h. v.a. in Bezug auf Punkt c) dann schätz diese Kovarianz besser. Zu Unrecht fixierte Fehlerkovarianzen können misfit verursachen (was gut ist, weil es so auffällt), aber ob das passiert hängt von den Ursachen der Fehlerkovarianz ab (diejenige, die durch omitted common causes, s.o., verursacht wurde) fällt leider nicht so schnell auf. Also: Wenn das Modell fittet schätze sie, damit der Effekt von G.w. auf EWOM nciht verzerrt wird.
Grüße
Holger
ich möchte mich meinen Vorschreibern anschließen.
Wichtig bei einem SEM ist, dass du dir der impliziten Annahmen/Restriktionen klar wirst, die du unbewusst oder bewusst ausdrückst:
a) Die beiden Sets von exogenen Variablen korrelieren nicht. Kannst du das wirklich annehmen? Ich halte das für gewagt und der Modellfit wird dir das zeigen.
Generell. Überleg dir ob diese Annahme für das, was du eigentlich ja testen willst, zentral ist. Manche Annahmen sind für die kausale Evidenz des zentralen Anliegens
wichtig / hilfreich, manche unsinnig. Die machen einem das Leben unnötig schwer
b) Die Messmodelle: Ein Messmodell unterstellt, dass die Kovarianzen der Indikatoren durch eine gemeinsame Ursache (die latente Variable) verursacht wurde. Außerdem
unterstellt es, dass die Kovarianzen zwischen den indikatoren der einen Variable und denen der anderen über die Kovarianzen / Effekte dieser latenten Variable laufen.
Sog. d-separation-Implikationen sind: Die Kovarianzen zwischen den Indikatoren einer Variable werden n.s., wenn du die latente Variable konstant hälst. Und die Kovarianzen
zwischen mit den Indikatoren der einen mit denen der anderen Variable werden n.s. wenn du eine der beiden Variablen konstant hälst. Harte Annahmen, die selten funktionieren,
weil der Teufel bei der item-formulierung im Detail liegt. Mit der Variation der Begrifflichkeit in den items hat man schnell eine andere latente Variable gemessen...
Schau dir daher die item-Formulierungen an und überlege, ob es wirklich Sinn macht, dass all diese items eine und dieselbe Variable messen. Denk daran, dass eine Variable eine
maximal spezifische Sache ist!
c) Die Effekte der linken exogenen Variablen auf EWOM sind auf 0 fixiert. Damit unterstellst du nicht nur, dass diese Variablen keinen Effekt haben, sondern auch, dass die empirischen Kovarianzen
zwischen diesen Variablen über ihre Verbindung über Glaubwürdigkeit laufen. Hälst du G.w. konsant, sinken sie auf 0. Das ist eine kausal wichtige Restriktion.
d) die Fehlerkovarianz zwischen G.w. und EWOM ist auf 0 fixiert. Damit unterstellst du dass es keine außerhalb des Modells befindlichen gemeinsamen Ursachen gibt. Wenn das Modell so fittet (d.h. v.a. in Bezug auf Punkt c) dann schätz diese Kovarianz besser. Zu Unrecht fixierte Fehlerkovarianzen können misfit verursachen (was gut ist, weil es so auffällt), aber ob das passiert hängt von den Ursachen der Fehlerkovarianz ab (diejenige, die durch omitted common causes, s.o., verursacht wurde) fällt leider nicht so schnell auf. Also: Wenn das Modell fittet schätze sie, damit der Effekt von G.w. auf EWOM nciht verzerrt wird.
Grüße
Holger
- Holgonaut
- Foren-Unterstützer

- Beiträge: 767
- Registriert: Do 2. Jun 2011, 18:20
- Danke gegeben: 3
- Danke bekommen: 207 mal in 198 Posts
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
Zurück zu Pfadanalyse, Strukturgleichungsmodelle & CFA
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 1 Gast