Hallo zusammen,
es geht um Folgendes:
Ich habe ein 2 (Gruppe) * 2 (Zeitpunkt --> Zwischendurch findet eine Art Training statt) Design und erhebe Reaktionszeiten auf auditive und visuelle Reize. Entweder wird ein Reiz unimodal (also nur visuell oder nur auditiv) oder bimodal präsentiert. Wenn die Reize bimodal präsentiert werden, dann können sie entweder zeitlich synchron oder asynchron präsentiert werden.
--> Es gibt somit insgesamt 13 Bedingungen:
1. Auditiv unimodal
2. Auditiv - 200 ms Pause - visuell
3. Auditiv - 100 ms Pause - visuell
4. Auditiv - 60 ms Pause - visuell
5. Auditiv - 30 ms Pause - visuell
6. Auditiv - 15 ms Pause - visuell
7. Auditv - visuell - synchron
8. Visuell - 15 ms Pause - auditiv
9. Visuell - 30 ms Pause - auditiv
10. Visuell - 60 ms Pause - auditiv
11. Visuell - 100 ms Pause - auditiv
12. Visuell - 200 ms Pause - auditiv
13. visuell unimodal
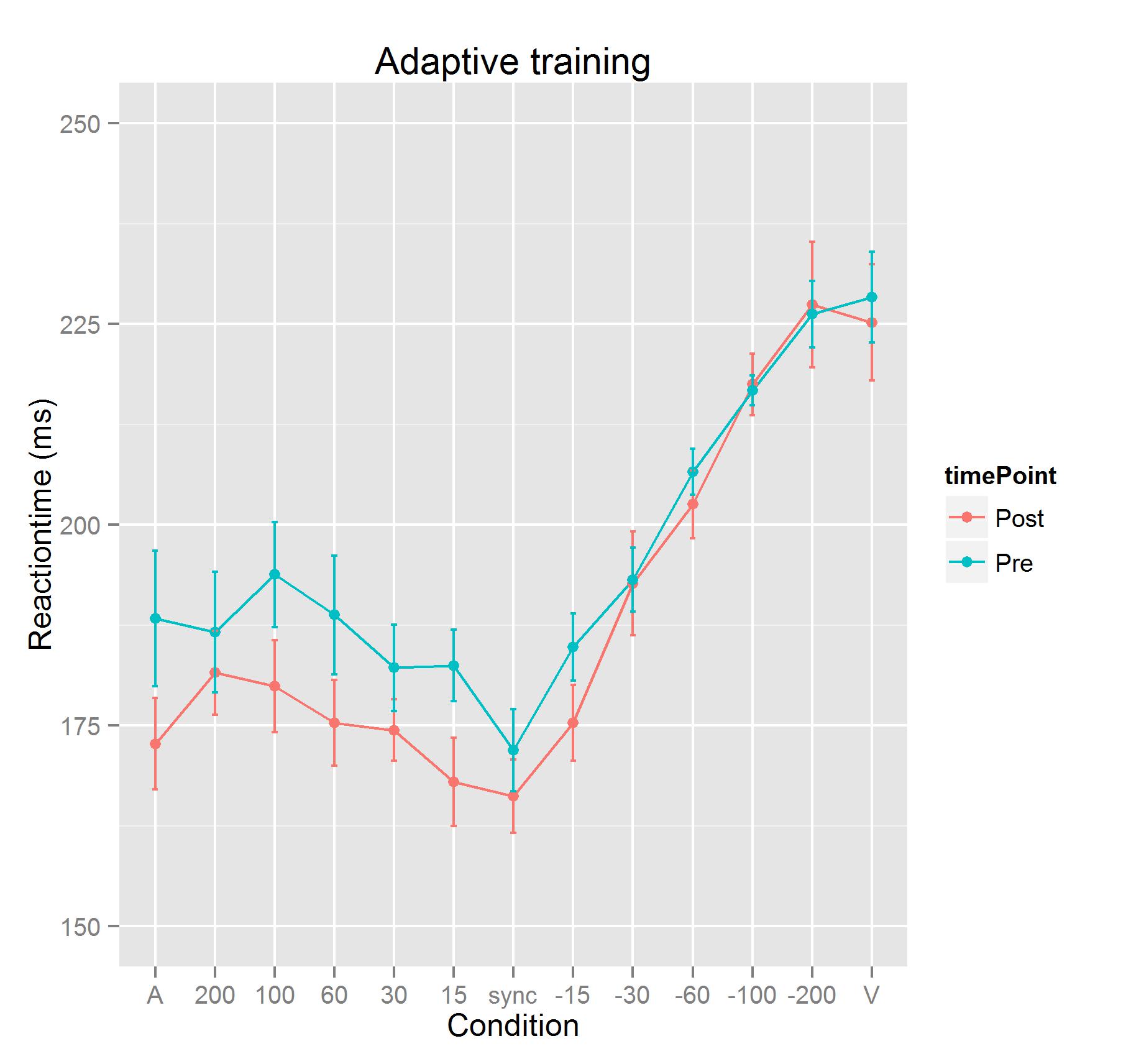
Im Anhang ist ein Graph zu sehen, der die Daten für eine Gruppe exemplarisch plottet. Die geplotteten Daten entsprechen nun leider nicht dem Originaldatensatz (ich erhebe noch) / der Hypothese und dienen nur zur Illustration, damit ihr euch ein besseres Bild machen könnt.
Hypothese:
Die Reaktionszeit verringert sich zum zweiten Messzeitpunkt für Bedingung 6,7, und 8 (möglicherweise sogar auch noch 5 und 9 ).
Für die Analyse können Bedingung 1 und 13 ausgeschlossen werden, da diese für etwas anderes verwendet werden.
Zunächst habe ich an ein GLM gedacht, in das ich alle übrigens 11 Bedingungen werfe, mit den Faktoren Zeit und Gruppe.
--> Problem: ich habe pro Gruppe nur 10 Probanden, somit wären das doch schon recht wenig Messpunkte, sehe ich das richtig?
Alternativ hätte ich nun zwei Regressionsgeraden berechnet: Eine für die linke und eine für die rechte "Seite" des Graphen und dort dann die Steigungen verglichen. Laut Hypothese müsste die Steigung im zweiten Messzeitpunkt steiler werden. WIE das nun aber geht, also mit welchem Verfahren das zu lösen ist, weiß ich nicht.
Hat jemand ansonsten noch eine andere Idee? Vielen Dank und beste Grüße,
RalfS.
Welches Verfahren sollte ich verwenden?
Welches Verfahren sollte ich verwenden?
- Dateianhänge
-
- Adaptive.jpg (140.41 KiB) 1274-mal betrachtet
- RalfS
- Beobachter

- Beiträge: 10
- Registriert: Do 8. Aug 2013, 10:15
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren sollte ich verwenden?
Hypothese:
Die Reaktionszeit verringert sich zum zweiten Messzeitpunkt für Bedingung 6,7, und 8 (möglicherweise sogar auch noch 5 und 9 ).
Dich interessieren nur diese 3 bzw. 5 Bedingungen,
und außerdem nicht Gruppeneffekte? Das wäre evtl.
eine Messwiederholungs-ANOVA mit den beiden
Messwiederholungsfaktoren Zeitpunkt (2 Stufen)
und Bedingung (5 Stufen).
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11368
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: Welches Verfahren sollte ich verwenden?
An sich interessieren mich nur diese 3-5 Bedingungen, das ist korrekt. Implizit ist natürlich in der Hypothese, dass die übrigen Bedingungen sich nicht verändern. Daher muss ich die also mit betrachten.
Die anova mit der Messwiederholung (repeated measures Anova, GLM ) ist wie gesagt etwas ungünstig, weli ich nur so wenig Probanden habe UND ich gleichzeitig alle 11 Bedinungen anschauen muss.
Viele Grüße!
Die anova mit der Messwiederholung (repeated measures Anova, GLM ) ist wie gesagt etwas ungünstig, weli ich nur so wenig Probanden habe UND ich gleichzeitig alle 11 Bedinungen anschauen muss.
Viele Grüße!
- RalfS
- Beobachter

- Beiträge: 10
- Registriert: Do 8. Aug 2013, 10:15
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren sollte ich verwenden?
An sich interessieren mich nur diese 3-5 Bedingungen, das ist korrekt. Implizit ist natürlich in der Hypothese, dass die übrigen Bedingungen sich nicht verändern. Daher muss ich die also mit betrachten.
Natürlich ist eigentlich gar nichts. Fragestellungen und Hypothesen
werden von Untersuchern aufgestellt. In der Hinsicht ist die Sache
hier etwas schwer nachvollziehbar. Dass sich etwas NICHT ändert
ist mit Signifikanztests schwer belegbar, zumindest bei kleinen
Stichproben. Eher kann man testen, ob die Veränderungen
zwischen t1 und t2 je nach Bedingung unterschiedlich stark sind
(Wechselwirkung Bedingung x Zeit).
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11368
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: Welches Verfahren sollte ich verwenden?
Da gebe ich dir Recht. Letztendlich geht es um die Wechselwirkung zwischen "Bedingungn" und "Zeitpunkt" -- und eigentlich auch "Gruppe".
Wenn ich nun also eine repeated-measures ANOVA rechne, mit 2 (Zeitpunkt) * 2 (Gruppe) * 11 (Bedingung) rechne, sind 10 Probanden pro Gruppe dann nicht viel zu wenig?
Wenn ja, welche Alternativen habe ich?
Wenn ich nun also eine repeated-measures ANOVA rechne, mit 2 (Zeitpunkt) * 2 (Gruppe) * 11 (Bedingung) rechne, sind 10 Probanden pro Gruppe dann nicht viel zu wenig?
Wenn ja, welche Alternativen habe ich?
- RalfS
- Beobachter

- Beiträge: 10
- Registriert: Do 8. Aug 2013, 10:15
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren sollte ich verwenden?
Ach so, doch mit Gruppe als einzubeziehendem Faktor?
Gesehen habe ich sowas schon oft; wüßte persönlich jetzt
nicht, dass das grundsätzlich gegen eine MW-ANOVA spräche.
Die power ist halt niedrig.
Mit freundlichen Grüßen
P.
Gesehen habe ich sowas schon oft; wüßte persönlich jetzt
nicht, dass das grundsätzlich gegen eine MW-ANOVA spräche.
Die power ist halt niedrig.
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11368
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: Welches Verfahren sollte ich verwenden?
Ansonsten würde ich zwei getrennte MW-ANOVA rechnen, für jede Gruppe eine, ich glaube, dass das nicht so ratsam ist.
Gibt es denn nicht die Möglichkeit eine Regressionsgerade für beide Seiten zu bilden (also rechts und links, wenn man den Graph in der Mitte teilt)? Dann hätte ich für jeden Probanden eine Steigung und ein Intercept. Ist es nicht möglich damit zu rechnen?
Oder alternativ, die Daten an ein Model zu fitten (bspw. Polynomial) und damit dann zu arbeiten?
Gruß,
RalfS.
Gibt es denn nicht die Möglichkeit eine Regressionsgerade für beide Seiten zu bilden (also rechts und links, wenn man den Graph in der Mitte teilt)? Dann hätte ich für jeden Probanden eine Steigung und ein Intercept. Ist es nicht möglich damit zu rechnen?
Oder alternativ, die Daten an ein Model zu fitten (bspw. Polynomial) und damit dann zu arbeiten?
Gruß,
RalfS.
- RalfS
- Beobachter

- Beiträge: 10
- Registriert: Do 8. Aug 2013, 10:15
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren sollte ich verwenden?
Oder alternativ, die Daten an ein Model zu fitten (bspw. Polynomial) und damit dann zu arbeiten?
Möglich wäre das, analog zum
. Mangrowth curve modeling
kann dann die individuellen Regressionsparameter als AVs nehmen.
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11368
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: Welches Verfahren sollte ich verwenden?
OK, hm, dann hätte ich also:
Linke Seite: Steigung als AV, für beide Messzeitpunkte
Rechte Seite: Steigung als AV, für beide Messzeitpunkte
Ein paar Fragen dazu:
Kann ich damit immer noch ein MW-ANOVA rechnen? Am Ende habe ich ja nur noch eine 2(zeitpunkt) * 2 (gruppe) * 1 (Steigung) repeated-measures Anova pro Seite...
Dann zur Steigung:
Bedingung 7 (synchrone Präsentation der Reize) werde ich somit doppelt verwenden. Die linke Seite beinhaltet Bedingung 2-7 und die rechte 7-12. Ist das aus deiner Sicht dennoch legitim?
Dann bin ich auch mit allen Fragen durch
Vielen Dank!
Linke Seite: Steigung als AV, für beide Messzeitpunkte
Rechte Seite: Steigung als AV, für beide Messzeitpunkte
Ein paar Fragen dazu:
Kann ich damit immer noch ein MW-ANOVA rechnen? Am Ende habe ich ja nur noch eine 2(zeitpunkt) * 2 (gruppe) * 1 (Steigung) repeated-measures Anova pro Seite...
Dann zur Steigung:
Bedingung 7 (synchrone Präsentation der Reize) werde ich somit doppelt verwenden. Die linke Seite beinhaltet Bedingung 2-7 und die rechte 7-12. Ist das aus deiner Sicht dennoch legitim?
Dann bin ich auch mit allen Fragen durch
Vielen Dank!
- RalfS
- Beobachter

- Beiträge: 10
- Registriert: Do 8. Aug 2013, 10:15
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren sollte ich verwenden?
Linke Seite: Steigung als AV, für beide Messzeitpunkte
Rechte Seite: Steigung als AV, für beide Messzeitpunkte
Mit linker Seite und rechter Seite kann ich leider nichts anfangen.
Ich verstehe mathematisch oder inhaltlich nicht recht den Sinn.
In der skizzierten Fragestellung finde ich nichts dahingehendes.
Ich dachte, dass individuell polynomiale Modelle aufgestellt werden
sollten, das war doch die vorherige Frage. Durchführbar wäre das.
Ob es dann zum Ziele führt bzw. durch Verwendung welcher weiteren
Analysen zum Ziele führt, kann ich leider nicht sagen, da ich
dazu inhaltlich viel mehr über die Studie wissen müsste, aber das
würde mir zu weit führen.
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11368
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 14 Gäste