STATISTIK-FORUM.de

[Wurzel1]

Hallo Leute,

ich habe folgendes Problem.

Gegeben ist der Erwartungswert = μ und Varianz = σ^2

Angenommen ich kenne den Wert für den Parameter μ. Ist der Schätzer für σ^2 = 1/n * (Xi - μ)^2 dann unverzerrt? Ich nehme an, dass es auf den Bias eine Auswirkung hat ob man den Erwartungswert kennt oder nicht.

aber wie kann ich dass beweisen?

Könnt ihr mir zeigen wie man dass schwarz auf weiß beweist?

Ich hoffe Ihr könnt mir weiter helfen

mfg

[DHA3000]

Schau dir mal die Formel genau an. Wenn du 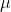kennst, was bleibt dann noch übrig, um 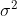nicht zu kennen?

[Wurzel1]

Ja eigentlich dann nichts mehr oder?

aber wie beweise ich dass dann im Unterricht?