ich bin aktuell mit der Auswertung einer Fahrsimulationsstudie beschäftigt und je mehr ich mich damit auseinandersetze, desto mehr frage ich mich ob ich die korrekten Verfahren gewählt habe. Ich versuche mal kurz Ziel und Design zu beschreiben. Auch wenn es leider viel Text ist hoffe ich sehr stark auf Hilfe, da ich momentan etwas mit meinem Latein am Ende bin.
Es soll untersucht werden, ob sich Fahrparameter (zB Standardabweichung Lenkwinkel) unterscheiden zwischen Phasen der Ablenkung (Faktor A: ohne Ablenkung; mit Ablenkung), zwischen Phasen unterschiedlicher Belastung (Faktor B: niedriger Workload, hoher Workload) und ob es eine Interaktion gibt. Das (ferne) Ziel ist, einen abgelenkten Fahrer allein anhand von Fahrparametern zu detektieren. Die Belastung als Faktor habe ich mit aufgenommen, da ich die Vermutung habe, dass sich eine hohe Belastung in den Fahrdaten ähnlich niederschlägt wie Ablenkung. Bei hoher Belastung kann, im Gegensatz zur Ablenkung, die Aufmerksamkeit voll auf der Fahraufgabe liegen --> Fahrsicherheit nicht/kaum beeinträchtigt.
Versuchsdesign ist komplett within-subject:
- Jeder Teilnehmer fuhr 2 Strecken mit jeweils 4 Messabschnitten. Von den Messabschnitten waren jeweils 2 mit Ablenkung (davon einmal bei 50 km/h, einmal bei 80 km/h) und 2 ohne Ablenkung (auch wieder 50 und 80 km/h)
- Faktor B (Workload) wurde durch die 2 Strecken umgesetzt - eine Strecke mit hohem streckeninduzierten Workload (Gegenverkehr, engere Fahrbahn etc.), eine mit niedrigem Workload
- Faktor A (Ablenkung) ist wie schon gesagt innerhalb der Strecken umgesetzt - pro Strecke 2 Messbereiche mit Ablenkung und 2 ohne (von den jeweils 2 immer einer bei 50 km/h, einer bei 80 km/h)
- somit habe ich von jedem Teilnehmer exakt 8 Durchschnittsgeschwindigkeiten
In Tabellenform zusammengefasst sieht ein Beispieldatensatz von einem der 40 Teilnehmer also so aus:
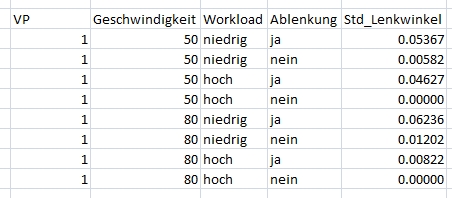
Ursprünglich wollte ich mit t-Tests für abhängige Stichproben untersuchen, ob es einen Effekt der Ablenkung gibt und mit einem weiteren t-Test einen Effekt des Workloads untersuchen. Problem: laut Shapiro-Wilk-Test sind die Wertedifferenzen nicht normalverteilt (Varianzenhomogenität ist allerdings gegeben laut Levene-Test).
Beim Recherchieren lese ich jetzt hin und wieder, dass man bei größeren Stichproben von Normalverteilung ausgehen kann, auch wenn diese laut statistischen Tests nicht gegeben.
zu den eigentlichen Fragen
- Frage 1: ist der t-Test für abhängige Stichproben hier überhaupt angebracht/sinnvoll?
- Frage 2: Stimmt die Aussage "Von Normalverteilung kann bei größeren Stichproben immer ausgegangen werden"?
- Frage 3: Wenn ja, aber welcher Gruppengröße? Bei mir wären es jeweils 160 pro Gruppe (pro Person 4 Messwerte von Messungen mit Ablenkung * 40 Probanden) - alllerdings jeweils immer 4 von derselben Person - spielt das hier eine Rolle?
Das gleiche Problem stellt sich mir, wenn ich die Interaktionseffekte untersuchen will. Mit meinem 2x2 Design wollte ich ursprünglich eine zweistufige ANOVA durchführen, Shapiro-Wilk-Tests sagen mir jedoch, dass keine Normalverteilung vorliegt. Bei den sich durch das 2x2 Design ergebenden 4 Gruppen (die jedoch dieselben Probanden enthalten!) hätte ich in jeder Gruppe exakt 80 Messwerte. Wie gesagt aber pro Gruppe immer 2 Messwerte derselben Person (einen vom 50 km/h Abschnitt, einen vom 80 km/h Abschnitt). Mein bisheriger Ansatz war daher, eine robuste Alternativmethode zu versuchen, die auf bootstrapping & M-estimators bzw. trimming beruht. Das genaue Verständnis dahinter übersteigt jedoch meine Fähigkeiten, in der Anwendugn halte ich mich an Andy Fields Buch "Discovering Statistics using R". Problem ist, dass die Methode für UNABHÄNGIGE Stichproben konzipiert ist. Für abhängige Stichproben mit repeated Measures wird keine Alternative geboten
- Frage 4: Kann ich die zweistufige ANOVA für meine Zwecke anwenden? gibt es ggf. robuste Alternativen, die auch die Messwiederholung berücksichtigen?
Viele Grüße




