STATISTIK-FORUM.de

[Naila]

Hallo Zusammen,

ich hoffe ihr könnt mir weiterhelfen in Sachen Stichprobengröße.

Wir wollen im Lager unsere Inventur auswerten, hinsichtlich Bestandsführung. Hierfür war die Idee gewesen, neben der eigentlichen Inventur, eine definierte Stichprobe monatlich zu inventieren. Hierbei ist jedoch die Frage: Wie groß sollte die Stichprobe sein? Wie viele Packstücke müssen wir inventieren, um eine aussagekräftige Auswertung zu machen? Im Durchschnitt haben wir 150.000 Packstücke im Lager.

Könnt ihr mir da helfen bzw. welche Infos fehlen noch, um mir eventuell helfen zu können?

Ich danke euch jetzt schon ganz doll!

Gruß

[bele]

Hallo Naila,

ich habe noch nie irgendwo Inventur gemacht und kann mir gerade nicht vorstellen, was da vor sich geht und was genau Du beantworten willst. Kannst Du das Problem bitte nochmal für Dumme erklären?

LG,
Bernhard

[mango]

Hallo, die Stichprobengröße richtet sich immer danach, was du messen möchtest. Wofür soll die Stichprobe groß genug sein?

[Naila]

Hallo Bernhard,

also bei einer Inventur werden alle im Lager vorhandenen Packstücke bzw. Lagerplätze physisch gezählt. Hierbei wird in einem System eine Inventur angelegt. Die gibt demjenigen, der zählt vor, welchen Lagerplatz er zählen soll. Die gezählte Menge wird dann anschließend an das System übertragen. Anschließend erfolgt ein Abgleich zwischen der gezählten Menge und der Menge, die laut System noch im Lager liegen sollte. Leider kommt es oft vor, dass die gezählte Menge mit der Systemmenge abweicht. Dies führt zu einer Inventurdifferenz. Die Artikel werden hier bei uns nicht an einem Tag gezählt, sondern es wird jeder Lagerplatz einmal im Jahr gezählt (darf auch öfter sein, aber mindestens einmal). Daher kann es sein, dass an einem Tag 100 Packstücke gezählt werden und am Tag danach 150. Da die Menge immer abweichend ist, wollen wir jetzt eine zusätzliche Inventur einführen - die Stichprobeninventur. Es soll also einmal im Monat immer die gleiche Menge gezählt werden. Die in der Stichprobe aufgetauchten Inventurdifferenzen werden dann ins Verhältnis zu der Stichprobengröße gesetzt. Und der errechnete Wert sollte dann für das ganze Lager stehen....Hierfür muss dann aber eben eine geeignete Stichprobengröße ausgewählt werden, um die Fehler auf das ganze Lager zu beziehen.

ich hoffe es ist etwas verständlicher geworden?!

Gruß
Naila

[Naila]

Hallo mango,

hat sich die Frage mit der vorhergehenden Antwort von mir vielleicht schon beantwortet?

[bele]

Hallo Naila,

mal sehen, wie gut mein Bild jetzt ist: Es gibt Packstücke und diese Packstücke sind auf Lagerplätze verteilt, wobei jedes Packstück genau einem Lagerplatz zugeordnet ist, jeder Lagerplatz aber mehrere Packstücke aufnehmen kann.
Du willst nun die Gesamtzahl der Packstücke schätzen, indem Du nur eine begrenzte Zahl von Lagerplätzen auszählst und von dieser begrenzten Zahl Lagerplätze auf alle Lagerplätze hoch rechnest.

Dazu wäre es am einfachsten anzunehmen, dass die Verteilung der Packstücke auf die Lagerplätze zufällig ist. Dass also in jedem Lager jede Sorte Packstück gleich wahrscheinlich vorkommt und dass die Differenz zwischen Sollmenge und Istmenge auf alle Lagerplätze gleich verteilt ist. Wäre das denn eine realistische Annahme, oder ist das falsch?
Können an jedem Lagerplatz beliebig viele Packstücke liegen oder ist das Lager immer mal wieder voll und mehr passt nicht hinein? Gibt es eine Sorte Packstücke oder gibt es viele verschiedene Sorten von Packstücken und wenn ja, wieviele? Welche Größenordnung von Packstücken verteilt sich auf welche Größenordnung von Lagerplätzen?

Du wirst am Schluss, darauf will mango hinaus, quantifizieren müssen, bei welchem Maß an Unsicherheit Dir die Schätzung "genau genug" ist. Ich schlage aber vor, dass wir erst das Problem genauer untersuchen, um ein rechnerisches Modell der Lagerwirklichkeit bauen zu können.

LG,
Bernhard

[Naila]

Hallo Bernhard,

danke schonmal, dass hier immer so schnell eine Antwort kommt.

Also es sind immer unterschiedlich viele Packstücke auf einem Lagerplatz und jeder Lagerplatz kann auch jedes Packstück annehmen. Das variiert dann je nach Größe des Packstückes und ob der Lagerplatz schon voll ist. Das kann man also nicht festlegen. Da gibt es keine systemseitigen Vorgaben. Das Lager ist auch bis jetzt nie voll, aber der Gesamtbestand kann mal nach oben und mal nach unten gehen. Derzeit haben wir im Schnitt 150.000 Packstücke im Lager liegen.

Ich habe bei einer weiteren Recherche einen Stichprobenrechner gefunden im Internet: http://www.bauinfoconsult.de/Stichproben_Rechner.html
ich habe folgende Zahlen eingetragen:
1. 5%
2. 99.99%
3. 150000
4. 50%

Würde das denn für meinen Fall Sinn ergeben? Es müssten dann 1500 Artikel gezählt werden, damit ich die Fehler auf das komplette Lager (150000) hochrechnen kann?

Gruß
Naila

[bele]

Hallo Naila,

kann schon sein, dass dieser online-Rechner für Dich irgendwie passend ist, ich habe Dein Vorgehen aber noch nicht verstanden. Ich hätte jetzt folgendes Gedacht: Wir haben 100 Lagerplätze mit gleicher Füllwahrscheinlichkeit. Wir zählen in 10 Lagerplätzen die Zahl der Teile aus, nehmen die mal 100/10=10 und schätzen damit die Anzahl der Packstücke in allen Lagerplätzen zusammen. Das kann man machen, weil die Zahl der Lagerplätze konstant ist.

Du hast meine Frage nicht beantwortet, ob es verschiedene Sorten von Packstücken gibt, ich nehme mal an das ist so. Jetzt willst Du anscheinend an 1000 Packstücken zählen, wie häufig welche Sorte Packstück ist und das mal 150.000/1000=150 nehmen, weil Du die Zahl 150.000 für konstant genug hälst. Verstehe ich das richtig?

LG,
Bernhard

[Naila]

Hey,

also um es mal einfacher zu machen, lassen wir die Lagerplätze einfach mal weg, weil die eigentlich irrelevant sind. Wir sagen zur Vereinfachung, dass wir 150.000 Packstücke im Lager haben auf einem großen Platz. Wie viele Packstücke müsste ich mir dann rausziehen und zählen, sodass ich die gezählten Abweichungen auf alle 150.000 beziehen kann? Wir möchten später zwar sagen, welche Lagerplätze angelaufen werden sollen, aber im Vordergrund steht die zu zählende Packstückanzahl.
Vereinfacht das die Sache?

Und ja es gibt verschiedene Packstücke. Es gibt unzählig verschiedene Artikel, die wir überall im Lager einlagern. Der Lagerort ist nicht vordefiniert für einen Artikel, was heißt, dass jeder Artikel auch je nach Platz auf jedem Lagerplatz liegen darf. Da gibt es keine Beschränkungen.

Gruß

[bele]

Hallo Naila,

das vereinfacht nicht sondern macht klar, was Du rechnen willst. Die 150.000 gelten also wirklich als Konstante. 150.000 ist eine sehr große Zahl und ich tue mal so, als ob sie unendlich groß wäre. Dann ziehst Du also eine Stichprobe der Größe n und darin befinden sich x Packstücke der Sorte 1. Der geschätze Anteil der Sorte 1 ist . Unser mathematisches Modell ist die sogenannte Binomialverteilung. 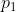Du weißt, wie groß der Anteil der Sorte 1 sein sollte.

Machen wir ein Beispiel. Sorte 1 kommt x=15 mal in einer Stichprobe von n=1000 vor, p sollte 0,018 sein. Jetzt lädst Du Dir aus dem Internet das Programm R herunter und gibst Folgendes ein:

Code: Alles auswählen

binom.test(x=15, n=1000, p=0.018)

Darauf wird R Dir wie folgt antworten:

Code: Alles auswählen

   Exact binomial test

data:  15 and 1000
number of successes = 15, number of trials = 1000, p-value = 0.5523
alternative hypothesis: true probability of success is not equal to 0.018
95 percent confidence interval:
0.00841905 0.02461970
sample estimates:
probability of success
                 0.015

Der p-Wert ist umso kleiner, je weniger Deine Zählung zu der angenommenen Häufigkeit von 1,8% passt. Mehr dazu unter https://de.wikipedia.org/wiki/P-Wert
Das 95%-Konfidenzintervall für den wahren Anteil reicht von 0,0084 bis 0,0246: https://de.wikipedia.org/wiki/Konfidenzintervall
Du kannst jetzt mit den bei Dir in Frage kommenden relativen Häufigkeiten durchprobieren, bei welchem n Dir die Konfidenzintervalle klein genug sind. In meinem Rechenbeispiel müsste man die Konfidenzintervallgrenzen mit 150.000 multiplizieren und erhält 1262 bis 3693 Stück. Das wird Dir zu unpräzise sein, so dass Du in diesem Beispiel ein größeres n haben wollen würdest.

Mehr zu den zugrundeliegenden Formeln und Rechenbeispiel ohne R: https://en.wikipedia.org/wiki/Population_proportion Die Formeln da kannst Du sonst bei Bedarf noch umstellen oder mit den Stichworten "Binomialverteilung Konfidenzintervall" herumspielen.

HTH,
Bernhard