Liebe Statistikprofis,
ich habe eine kurze Frage zur Ergebnisinterpretation von Werten, welche mit einem mittels WLS errechneten Schätzmodell berechnet wurden.
Meine Frage: Muss ich die (mittels WLS-Modell) errechneten Schätzwerte nochmals (zurück-)transformieren, da ich ja die abhängige und unabhängige Variable vorab mittels Gewichten transformiert habe?
Ausgangssituation: Ich habe mittels einfacher linearer Regression (OLS in R; Befehl: lm) ein Modell errechnet, bei welchem die Anzahl abzusetzender Traktoren in Stück (abhängige Variable) über die Fläche an Ackerland in Hektar (unabhängige Variable) geschätzt wird. Beide Variablen wurden als Querschnitt auf Landkreisebene erhoben, mit n = 389.
Die unabhängige Variable ist mit einem P-Wert von <0,05 signifikant und das R2 mit 0,73, wie auch das adjustierte R2 mit 0,73 sehen gut aus. Der P-Wert des F-Tests ist auch <0,05 und somit signifikant.
Leider habe ich bei der Überprüfung der Annahmen des Gauß-Markov-Theorems Heteroskedastizität festgestellt. Diese konnte ich mittels WLS beheben.
Dazu habe ich beide Variablen zur Gewichtung durch sqrt(Residuen des ursprünglichen Modells) geteilt und anschließend mit den gewichteten Variablen wieder ein neues Schätzmodell per OLS berechnet.
Anmerkung/ meine Gedanken dazu:Ich habe schon einige Quellen zu der Thematik durchforstet aber nirgendswo stand irgendwas von einer Art "Rück"-Transformation der geschätzten Werte. Da ja durch meine Vorgehensweise einzelne Datenpunkte "nur" mittels Residuen gewichtet wurden, dürfte eigentlich keine Transformation nötig sein. Ich frage trotzdem, da ich von jemandem bezüglich dieser Frage sehr verunsichert wurde und ich daher nochmal Profis zur Rate ziehen wollte.
Falls noch Informationen fehlen, oder ich bei meiner Suche im Forum eine bereits vorhandene Antwort auf meine Frage übersehen habe, gebt mir einfach einen Hinweis.
Vielen Dank!
Weighted least squares - Ergebnisse nochmal transformieren?
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
- GuybrushT
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 23. Jul 2016, 12:59
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Weighted least squares - Ergebnisse nochmal transformier
Also, du hast aus

folgendes gemacht:
 .
.
Und, ändern sich und
und 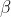 dadurch?
dadurch?
Die Transformation ist übrigens nicht wirklich standard. Normalerweise teilt man durch oder
oder  .
.
folgendes gemacht:
Und, ändern sich
Die Transformation ist übrigens nicht wirklich standard. Normalerweise teilt man durch
- DHA3000
- Elite

- Beiträge: 478
- Registriert: So 8. Jul 2012, 15:08
- Danke gegeben: 0
- Danke bekommen: 62 mal in 62 Posts
Re: Weighted least squares - Ergebnisse nochmal transformier
Ja, so ähnlich!
Ich habe anstatt mit u^2 mit Wurzel(u) gewichtet, also anstatt des üblichen Wurzel(x) habe ich Wurzel(u) als Gewicht probiert.
Ich weiß, dass man üblicherweise mit Hilfe von x oder Wurzel(x) gewichtet, so steht es auch überall beispielhaft in der Literatur. Allerdings hat Wurzel(x) beim ausprobieren zwar eine Verbesserung der Testergebnisse erbracht, es reichte aber nicht aus um nach der Transformation Hinweise auf Homoskedastizität zu liefern (ich hab mit dem Breusch-Pagan-Test gearbeitet). Ich dachte dann, ich probiere es einfach mal mit Wurzel(u). Das brachte den erwünschten Effekt.
Alpha verringerte sich bei der Gewichtung mit Wurzel(u) um 0,3995339, Beta erhöhte sich um 0,000003017. (Bei der üblichen Gewichtungsmethode mit Wurzel(x) veränderte sich Alpha um 0,01440536 und Beta um 0,0000057). Dazu ist noch zu erwähnen, dass Alpha vor und nach den Transformationen nicht signifikant war (ist für meine Untersuchung auch nicht wichtig), Beta war vorher und nachher jeweils signifikant.
Ich habe anstatt mit u^2 mit Wurzel(u) gewichtet, also anstatt des üblichen Wurzel(x) habe ich Wurzel(u) als Gewicht probiert.
Ich weiß, dass man üblicherweise mit Hilfe von x oder Wurzel(x) gewichtet, so steht es auch überall beispielhaft in der Literatur. Allerdings hat Wurzel(x) beim ausprobieren zwar eine Verbesserung der Testergebnisse erbracht, es reichte aber nicht aus um nach der Transformation Hinweise auf Homoskedastizität zu liefern (ich hab mit dem Breusch-Pagan-Test gearbeitet). Ich dachte dann, ich probiere es einfach mal mit Wurzel(u). Das brachte den erwünschten Effekt.
Alpha verringerte sich bei der Gewichtung mit Wurzel(u) um 0,3995339, Beta erhöhte sich um 0,000003017. (Bei der üblichen Gewichtungsmethode mit Wurzel(x) veränderte sich Alpha um 0,01440536 und Beta um 0,0000057). Dazu ist noch zu erwähnen, dass Alpha vor und nach den Transformationen nicht signifikant war (ist für meine Untersuchung auch nicht wichtig), Beta war vorher und nachher jeweils signifikant.
- GuybrushT
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 23. Jul 2016, 12:59
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Weighted least squares - Ergebnisse nochmal transformier
Wie soll das denn funktionierten, wenn  negativ ist? Was ohne Zweifel der Fall ist.
negativ ist? Was ohne Zweifel der Fall ist.
Wie du der obigen Theorie entnehmen kannst, kann sich nicht verändern. Die Werte müssen identisch sein.
nicht verändern. Die Werte müssen identisch sein.
Irgendwas machst du also fundamental falsch.
Wie du der obigen Theorie entnehmen kannst, kann sich
Irgendwas machst du also fundamental falsch.
- DHA3000
- Elite

- Beiträge: 478
- Registriert: So 8. Jul 2012, 15:08
- Danke gegeben: 0
- Danke bekommen: 62 mal in 62 Posts
Re: Weighted least squares - Ergebnisse nochmal transformier
Entschuldige, ich hatte vergessen zu erwähnen, dass ich u vorab mit der Betragsfunktion in rein positive Werte umgewandelt habe. Ich weiß natürlich, dass ich keine Wurzel aus negativen Werten ziehen kann.
- GuybrushT
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 23. Jul 2016, 12:59
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Weighted least squares - Ergebnisse nochmal transformier
Inzwischen habe ich eine Lösung für mein Problem gefunden. 
- GuybrushT
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 23. Jul 2016, 12:59
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 2 Gäste


