Liebe Community
Ganz grob ist die Situation wie folgt:
Wir beziehen Impulse von zahlreichen (> 500) verschiedenen Quellsystemen, auf die wir keinen Zugriff haben. D.h. wir nehmen entgegen, was eingeliefert wird, wir können aber keine Einlieferung eines Impulses anfordern oder beeinflussen. In Summe sind es ca. 40 Mio. Impulse pro Tag, die über den Tag nicht gleichverteilt sind. Unsere Zielsetzung ist nun, dass wir sehr schnell erkennen (nach Möglichkeit im Minutenbereich), wenn eine (oder mehrere) unserer Quellen nicht mehr liefert.
Den Eingang der Impulse in einem fixen Zeitraum t-fix (etwa 30 oder 60 Sekunden) können wir als Poisson-verteilt annehmen und wegen der grossen Volumen durch die Normalverteilung annähern.
Nehmen wir nun die Nullhypothese an, die besagt, dass wir im Zeitraum t-fix mindestens 40'000 Impulse erreichen/erwarten (und alles wäre ok), dann wäre die Alternativhypothese, dass wir zu wenig Impulse haben bzw. (zumindest) eine Quelle nicht (ausreichend) liefert. Die Verteilungsfunktion der Normalverteilung besagt, dass bei einem Erwartungswert von 40'000 99,75% der Messwerte im Intervall zwischen 39485 = 40'000 - 515 (2,576 * Sigma mit Sigma = 200 = Wurzel von 40'000) und unendlich liegen. Nach meinem Verständnis ist das in diesem Fall auch die Irrtumswahrscheinlichkeit, d.h. mit einer Wahrscheinlichkeit von 0,25% verwerfe ich die Nullhypothese und suche nach einer nichtliefernden Quelle, obwohl alles in Ordnung ist.
In der Praxis ergeben sich nun aber mehrere Herausforderungen:
1. Der Erwartungswert lässt sich nicht mit dieser Präzision abschätzen. Wenn ich oben 40'000 Impulse genannt habe, dann können es auch 37'000 sein. dann aber wären die 39485 als untere Grenze völlig daneben.
2. Der Erwartungswert verhält sich im Tagesverlauf ähnlich einer Sinuskurve (halbe Periode). D.h. es gibt nur sehr kurze Zeiträume, in denen der Erwartungswert vergleichbar hoch ist.
3. Den Untersuchungszeitraum t-fix kann ich nicht beliebig verlängern. Ich will bekanntlich im Minutenbereich (10-20 Minuten) reagieren.
Und hier bin ich mit meinem Latein am Ende. Hat jemand eine Idee, wie ich die Problematik in den Griff bekommen kann?
Vielen Dank im Voraus für alle anregenden und konstruktiven Beiträge.
Geeignetes Verfahren ?
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
- xJQvVDWe
- Grünschnabel

- Beiträge: 3
- Registriert: Sa 6. Jan 2018, 17:53
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Geeignetes Verfahren ?
Hallo Viele-Buchstaben,
Bitte erläutere, warum sich, bei 40 Mio Ereignissen am Tag, die Ereignisrate nicht sehr, sehr genau bestimmen lässt. Liegt es daran, dass die Schwankungen über den Tag hinweg auftreten oder gibt darüber hinaus weitere Störgrößen, die nicht bekannt sind? Die zugrundeliegende Poisson-Rate für jede Minute
für jede Minute 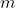 sollte sich doch binnen weniger Tage bestimmen lassen? (Der Tag hat 1440 Minuten, da erwarten wir fast 28000 Ereignisse pro Minute. Nehmen wir an, in einer weniger frequentierten Minute kommen nur 20000 Ereignisse vor. Beobachtest Du nur einmal 20000 Ereignisse in dieser Minute, dann reicht das 99,75%-Konfidenzintervall für die wahre Rate bei 19575 - 20431. Machst Du das mehrere Tage hintereinander, wird die Rate für jede einzelne Minute des Tages sehr rasch, sehr präzise zu bestimmen sein.)
sollte sich doch binnen weniger Tage bestimmen lassen? (Der Tag hat 1440 Minuten, da erwarten wir fast 28000 Ereignisse pro Minute. Nehmen wir an, in einer weniger frequentierten Minute kommen nur 20000 Ereignisse vor. Beobachtest Du nur einmal 20000 Ereignisse in dieser Minute, dann reicht das 99,75%-Konfidenzintervall für die wahre Rate bei 19575 - 20431. Machst Du das mehrere Tage hintereinander, wird die Rate für jede einzelne Minute des Tages sehr rasch, sehr präzise zu bestimmen sein.)
Willst Du in 10 Minuten reagieren, kannst Du den Tag vielleicht stattdessen in 144 10-Minuten-Intervalle unterteilen und wenn Du in einem einzigen solchen Intervall 200000 Ereignisse beobachtest, hast Du schon ein schmales 99,75%-KI von 198650 - 201356.
Wenn Du das mit dem Sinus ernst meinst, könnte man die Poissonrate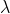 auch modellieren als
auch modellieren als  = sin(c_1*(t+c_2)+c_3) . Ich bin recht sicher, dass sich
. Ich bin recht sicher, dass sich 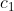 ,
, 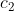 und
und 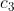 mit den 40 Mio Beobachtungen an einem Tag recht fix sehr(!) präzise bestimmen lassen.
mit den 40 Mio Beobachtungen an einem Tag recht fix sehr(!) präzise bestimmen lassen.
LG,
Bernhard
xJQvVDWe hat geschrieben:Den Eingang der Impulse in einem fixen Zeitraum t-fix (etwa 30 oder 60 Sekunden) können wir als Poisson-verteilt annehmen und wegen der grossen Volumen durch die Normalverteilung annähern.
[...]
1. Der Erwartungswert lässt sich nicht mit dieser Präzision abschätzen. Wenn ich oben 40'000 Impulse genannt habe, dann können es auch 37'000 sein. dann aber wären die 39485 als untere Grenze völlig daneben.
2. Der Erwartungswert verhält sich im Tagesverlauf ähnlich einer Sinuskurve (halbe Periode). D.h. es gibt nur sehr kurze Zeiträume, in denen der Erwartungswert vergleichbar hoch ist.
Bitte erläutere, warum sich, bei 40 Mio Ereignissen am Tag, die Ereignisrate nicht sehr, sehr genau bestimmen lässt. Liegt es daran, dass die Schwankungen über den Tag hinweg auftreten oder gibt darüber hinaus weitere Störgrößen, die nicht bekannt sind? Die zugrundeliegende Poisson-Rate
Willst Du in 10 Minuten reagieren, kannst Du den Tag vielleicht stattdessen in 144 10-Minuten-Intervalle unterteilen und wenn Du in einem einzigen solchen Intervall 200000 Ereignisse beobachtest, hast Du schon ein schmales 99,75%-KI von 198650 - 201356.
Wenn Du das mit dem Sinus ernst meinst, könnte man die Poissonrate
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Geeignetes Verfahren ?
Hallo Bernhard
Vielen Dank für deine Bereitschaft die Diskussion zu bereichern.
Da habe ich mich wohl etwas missverständlich ausgedrückt. Die Historie kennen wir sehr gut, diese können wir auch auswerten.
Aber die Impulse haben ihren Ursprung im Verbraucherverhalten. Und da weichen die Volumina von einem Tag zum anderen leicht mal um 15% oder 20% ab, ohne dass irgendetwas schief läuft. Der Mensch macht halt an einem Regentag etwas anderes als an einem Sonnentag.
Den Hinweis auf die Sinuskurve darf man nicht wortwörtlich nehmen. Ich wollte einfach nur ausdrücken, dass die Volumina von der Nacht weg ansteigen, dann im Tagesverlauf irgendwann einen Spitzenwert erreichen und zur Nacht hin wieder abnehmen. Deswegen ist mein Erwartungswert um 6:36 Uhr deutlich niedriger als um 13:14 Uhr.
FG,
Ralf
Vielen Dank für deine Bereitschaft die Diskussion zu bereichern.
Da habe ich mich wohl etwas missverständlich ausgedrückt. Die Historie kennen wir sehr gut, diese können wir auch auswerten.
Aber die Impulse haben ihren Ursprung im Verbraucherverhalten. Und da weichen die Volumina von einem Tag zum anderen leicht mal um 15% oder 20% ab, ohne dass irgendetwas schief läuft. Der Mensch macht halt an einem Regentag etwas anderes als an einem Sonnentag.
Den Hinweis auf die Sinuskurve darf man nicht wortwörtlich nehmen. Ich wollte einfach nur ausdrücken, dass die Volumina von der Nacht weg ansteigen, dann im Tagesverlauf irgendwann einen Spitzenwert erreichen und zur Nacht hin wieder abnehmen. Deswegen ist mein Erwartungswert um 6:36 Uhr deutlich niedriger als um 13:14 Uhr.
FG,
Ralf
- xJQvVDWe
- Grünschnabel

- Beiträge: 3
- Registriert: Sa 6. Jan 2018, 17:53
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Geeignetes Verfahren ?
Da die Angaben zum Problem reichlich geheimnisvoll und zudem unzuverlässig sind, muss man sich
einiges zusammenreimen und muss leider viel herumraten.
Wenn der prozentuale bzw. absolute Abfall zwischen einem Intervall tx und tx+1 ein ungewöhnliches
Ausmaß animmt, könnte das ein Indiz für einen Ausfall sein.
Allerdings handelt es sich hier um eine diagnostische Prozedur. Einfach jeden Abfall aus dem Endbereich
der Verteilung - wie im Beispiel 0,25% - als Ausfall zu diagnostizieren, wirft das Problem auf, dass bei jeder
400. Betrachtung eines regelhaften Geschehens zwangsläufig eine falsch-positive Ausfalldiagnose auftritt.
Das wäre nicht schlimm, wenn echte Ausfälle weitaus häufiger wären und/oder wenn eine falsch-positive
Diagnose wenig Schäden verursacht und/oder falsch-negatvie Annahmen vermnieden werden sollen.
Man bräuchte, um diagnostische Regeln (wie den cutoff-Wert für die Anahme eines Ausfalls) aufstellen zu können,
Validierungsdaten - Verläufe, bei denen gesichert ist, dass ein Ausfall vorlag. Und die Grundrate an Ausfällen
über einen bestimmten Zeitraum, um Risiken falsch-positiver und falsch-negativer Entscheidungen schätzen
zu können. Letztlich der ganze Apparat - Sensitivität, Spezifität, Positve und Negative Predictive Power
bei diversen Cutoffs, abgewogen gegen Nutzen/Schaden richtiger/falscher Entscheidungen.
Mit freundlichen Grüßen
PonderStibbons
einiges zusammenreimen und muss leider viel herumraten.
Wenn der prozentuale bzw. absolute Abfall zwischen einem Intervall tx und tx+1 ein ungewöhnliches
Ausmaß animmt, könnte das ein Indiz für einen Ausfall sein.
Allerdings handelt es sich hier um eine diagnostische Prozedur. Einfach jeden Abfall aus dem Endbereich
der Verteilung - wie im Beispiel 0,25% - als Ausfall zu diagnostizieren, wirft das Problem auf, dass bei jeder
400. Betrachtung eines regelhaften Geschehens zwangsläufig eine falsch-positive Ausfalldiagnose auftritt.
Das wäre nicht schlimm, wenn echte Ausfälle weitaus häufiger wären und/oder wenn eine falsch-positive
Diagnose wenig Schäden verursacht und/oder falsch-negatvie Annahmen vermnieden werden sollen.
Man bräuchte, um diagnostische Regeln (wie den cutoff-Wert für die Anahme eines Ausfalls) aufstellen zu können,
Validierungsdaten - Verläufe, bei denen gesichert ist, dass ein Ausfall vorlag. Und die Grundrate an Ausfällen
über einen bestimmten Zeitraum, um Risiken falsch-positiver und falsch-negativer Entscheidungen schätzen
zu können. Letztlich der ganze Apparat - Sensitivität, Spezifität, Positve und Negative Predictive Power
bei diversen Cutoffs, abgewogen gegen Nutzen/Schaden richtiger/falscher Entscheidungen.
Mit freundlichen Grüßen
PonderStibbons
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11372
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: Geeignetes Verfahren ?
Hallo Ralf,
die neuerlichen Ausführungen machen das Problem verständlich. Du willst den Ausfall von einer von mehr als 500 Signalquellen, also ca 1/500 = 0,2% der Signale erkennen, wenn das Rauschen 15 bis 20 % beträgt. Ich befürchte, Du musst Dich nach einem anderen Indikator als der Signalhäufigkeit umsehen, wenn Dir nicht noch weitere Annahmen einfallen, die man belastbar einbeziehen kann, um die 0,2%-Schwankungen von den 20%-Schwankungen binnen 10-20 Minuten zu unterscheiden.
LG,
Bernhard
die neuerlichen Ausführungen machen das Problem verständlich. Du willst den Ausfall von einer von mehr als 500 Signalquellen, also ca 1/500 = 0,2% der Signale erkennen, wenn das Rauschen 15 bis 20 % beträgt. Ich befürchte, Du musst Dich nach einem anderen Indikator als der Signalhäufigkeit umsehen, wenn Dir nicht noch weitere Annahmen einfallen, die man belastbar einbeziehen kann, um die 0,2%-Schwankungen von den 20%-Schwankungen binnen 10-20 Minuten zu unterscheiden.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Geeignetes Verfahren ?
Hallo Bernhard, hallo PonderStibbons
Vielen Dank. Das hat mir doch schon sehr geholfen.
In der Tat, da die Signalhäufigkeit sich eigentlich gar nicht präzise genau prognostizieren lässt, ist sie als Erwartungswert ungeeignet. Das lässt sich wohl a posteriori mit statistischen Mitteln auch nicht mehr heilen.
Wir brauchen also eine andere Grösse. Der Zuwachs könnte vielleicht eine sein. Dann werden wir nun mal in unseren Daten schauen, ob wir so etwas finden.
FG, Ralf
Vielen Dank. Das hat mir doch schon sehr geholfen.
In der Tat, da die Signalhäufigkeit sich eigentlich gar nicht präzise genau prognostizieren lässt, ist sie als Erwartungswert ungeeignet. Das lässt sich wohl a posteriori mit statistischen Mitteln auch nicht mehr heilen.
Wir brauchen also eine andere Grösse. Der Zuwachs könnte vielleicht eine sein. Dann werden wir nun mal in unseren Daten schauen, ob wir so etwas finden.
FG, Ralf
- xJQvVDWe
- Grünschnabel

- Beiträge: 3
- Registriert: Sa 6. Jan 2018, 17:53
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 6 Gäste


