STATISTIK-FORUM.de

[Elisabeta]

Hallo,

bei den Daten, die ich untersuchen möchte, gibt es Parameter, die normalverteilt sind und welche, die erst nach dem Logarithmieren normalverteilt sind.
Wie gehe ich mit den logarithmierten Parametern um?
Muss ich bei der deskriptiven Statikstik, wenn ich mir zB den Mittelwert ausrechnen lasse, wieder "zurückrechnen", um mit dem Mittelwert eines von Anfang an normalverteilten Parameters vergleichen zu können? Was mache ich mit der Standardabweichung? Rechne ich die auch um den gleichen Faktor zurück?
Wenn ich eine Varianzanalyse machen will, was gilt es zu beachten, wenn logarithmierte und nicht logarithmierte Parameter untersucht werden?

Ich freue mich auf Antworten und bin dankbar für die Hilfe !

[PonderStibbons]

bei den Daten, die ich untersuchen möchte, gibt es Parameter, die normalverteilt sind und welche, die erst nach dem Logarithmieren normalverteilt sind.
Wie gehe ich mit den logarithmierten Parametern um?

Warum und wozu hast Du die Daten transformiert, warum und wozu interessiert Dich
"Normalverteilung" (und konkret wessen Normalverteilung)? Verfahren des allgemeinen
linearen Modells wie die Varianzanalyse verlangen keine Normalverteilung der
abhängigen Variablen, falls das gemeint war. Wie sehen denn Thema, Fragestellung,
Erhebungsdesign, erhobene Variablen Deiner Studie aus, und wie groß ist Deine Stichprobe?

Mit freundlichen Grüßen

PonderStibbons

[bele]

Hallo Elisabeta,

gegeben seien die Zahlen 1 bis 50. Deren Mittewert ist 25,5. Der Mittelwert ihrer natürlichen Logarithmen ist 2,97. Zurückrechnen? .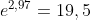
Wenn Du also den Mittelwert der Logarithmen zurückrechnest, kommt keinesfalls der Mittelwert der Ursprungszahlen heraus. Du musst Dir also sehr gut überlegen, was du warum logarithmierst und musst dann die beiden Welten fortan sauber getrennt halten.
Logarithmieren sollte nicht als Reflex und nicht um zwanghaften Streben noch überflüssiger Normalverteilung erfolgen.

HTH,
Bernhard

[Elisabeta]

Hallo,

vielen Dank für die schnellen Antworten!
Meine Gesamtgruppe (lungenkranke Menschen, die eine Lungenspülung erhalten haben), umfasst etwa 3000 Datensätze.
Es gibt drei interessierende Krankheiten, Datensätze von Menschen mit diesen Krankheiten sind aus der Gesamtgruppe herausgesucht worden.
(Krankheit 1 n = 97, Krankheit 2 n = 67, Krankheit 3 n = 25)
Es sind durchflusszytometrisch die Anteile von verschiedenen Zellen in der Lungenspülflüssigkeit erhoben worden ( 25 metrisch skalierte Parameter,meist nicht normalverteilt), dazu Alter bei Untersuchung und noch kategoriale Parameter (Geschlecht, Nikotinkonsum, Therapie/Ansprechen auf die Therapie).
Ich arbeite mit SPSS und hatte auch schon eine Statistikberatung an der Uni, bei der vorgeschlagen wurde, die nicht normalverteilten Variablen zu logarithmieren und dann so damit weiterzumachen, damit ich Tests machen kann, die eine Normalverteilung voraussetzen (t-Test).
Nun soll ich zunächst zur Übersicht Mittelwerte und Standardabweichungen für die metrisch skalierten Parameter der Gruppen (Krankheit 1,2,3 und Gesamtgruppe) in einer Tabelle darstellen. Dafür müsste ich die nicht normalverteilten Variablen ja noch nicht logarithmieren, bloß ist der Mittelwert bei schief verteilten Daten eine sinnvolle Angabe? Hier wäre ja der Median besser, aber dann wären manche Variablen mit Mittelwert und Standardabweichung beschrieben und andere nicht. Deshalb hatte ich mich gefragt, ob man doch die nicht normalverteilten Variablen hier logarithmieren sollte.
Danach soll mittels einfaktorieller Varianzanalyse ein Mittelwertvergleich erfolgen (und später auch der Einfluss von kategorialen Variablen untersucht werden). Hier sollte laut meinen Statistikbüchern Varianzhomogenität vorliegen, was aber laut Levene-Test oft nicht gegeben ist (auch nicht mit den logarithmierten Daten). Außerdem sollte die abhängige Variable innerhalb der Gruppen normalverteilt sein, was aber oft auch nicht so ist (aber ab ca 20 Personen sollen Verletzungen nicht so schlimm sein..) Bei der Beratung wurde mir mitgeteilt, dass man sehr vorsichtig in der Auswertung von Varianzanalysen sein muss, wenn logarithmierte und nicht logarithmierte Daten darin vorkommen (aber wie genau man vorgehen muss, ist leider nicht erklärt worden..)

Deshalb bin ich ziemlich verwirrt, welche Tests ich mit welchen Daten (logarithmierte Form oder ursprüngliche, nicht normalverteilte Form) durchführen darf.
Vielleicht sollte ich einfach auf nichtparametrische Tests ausweichen?

Vielen Dank für die Hilfe und das Interesse an meinem Problem, habe mich über die Antworten gefreut : )

[PonderStibbons]

Ich arbeite mit SPSS und hatte auch schon eine Statistikberatung an der Uni, bei der vorgeschlagen wurde, die nicht normalverteilten Variablen zu logarithmieren und dann so damit weiterzumachen, damit ich Tests machen kann, die eine Normalverteilung voraussetzen (t-Test).

t-Tests erfordern keine normalverteilten Daten. Allenfalls innerhalb der beiden
Gruppen sollten die Werte aus Normalverteilungen stammen. Aber auch das ist
nur bei kleinen Stichproben der Fall. Bei n > 90 (wie hier beim Vergleich der
beiden kleinsten Stichproben) brauchst Du Dir um "Normalverteilung" für
die Gültigkeit des Tests keine Gedanken zu machen, bei ausreichend großen
Stichproben ist der Tests robust.

Eine andere Frage ist, ob bei solchen biologischen Parametern nicht üblicherweise,
aus inhaltlichen Gründen logarithmiert wird. Zum Beispiel, wenn es sich um
Wachstumsprozesse handelt, zu der einfache, lineare Betrachtungen nicht passen.
Das ist aber eine substanzwissenschaftliche Frage und hat nichts mit Normalverteilung
zu tun.

Dafür müsste ich die nicht normalverteilten Variablen ja noch nicht logarithmieren, bloß ist der Mittelwert bei schief verteilten Daten eine sinnvolle Angabe?

Mittelwert und Standardabweichung und Minimum und Maximum und Median wären Angaben,
aus deren Gesamtheit sich ein brauchbares Bild ergibt.

Danach soll mittels einfaktorieller Varianzanalyse ein Mittelwertvergleich erfolgen (und später auch der Einfluss von kategorialen Variablen untersucht werden). Hier sollte laut meinen Statistikbüchern Varianzhomogenität vorliegen, was aber laut Levene-Test oft nicht gegeben ist (auch nicht mit den logarithmierten Daten).

Dafür gibt es in SPSS die Korrekturen nach Welch bzw Brown-Forsythe.

Außerdem sollte die abhängige Variable innerhalb der Gruppen normalverteilt sein, was aber oft auch nicht so ist (aber ab ca 20 Personen sollen Verletzungen nicht so schlimm sein..)

Man kann es auch einfacher haben und sich die Verteilung der Vorhersagefehler (Residuen) aus
der Varianzanalyse ansehen. Diese Residuen sollten vorzugsweise aus einer Normalverteilung
stammen, aber bei einer Stichprobengröße von Gesamt n = 189 ist die Analyse auch dann korrekt,
wenn davon abgewichen wird.

Bei der Beratung wurde mir mitgeteilt, dass man sehr vorsichtig in der Auswertung von Varianzanalysen sein muss, wenn logarithmierte und nicht logarithmierte Daten darin vorkommen (aber wie genau man vorgehen muss, ist leider nicht erklärt worden..)

Wie gesagt, nirgends ist eine erkennbar eine Normalverteilung von was auch immer
erforderlich, Du könntest durchgehend ohne Transformation rechnen. Aber es könnte
sein, dass es um biologische Prozesse geht, die nahelegen, dass Du von vornherein die
meisten Deiner Variablen logarithmieren willst.


Mit freundlichen Grüßen

PonderStibbons

[Elisabeta]

Hallo PonderStibbons,

ich danke Dir für Deine Hilfe!! Du hast meinen Tag gerettet.
Damit sind fast alle meine Fragen beantwortet : )
Eine bleibt noch: Kann ich die Varianzanalyse durchführen, wenn ich dabei Mittelwerte von einer Variable vergleiche, die in der einen Gruppe normalverteilt war, aber in den anderen log-normalverteilt ist? Könnte ich einfach alle Variablen logarithmieren (auch die, die es nicht bräuchten), um das einheitlich zu haben?

Vielen, vielen Dank !!!

[PonderStibbons]

Eine bleibt noch: Kann ich die Varianzanalyse durchführen, wenn ich dabei Mittelwerte von einer Variable vergleiche, die in der einen Gruppe normalverteilt war, aber in den anderen log-normalverteilt ist?

So exakt ist doch weder das eine noch das andere belegbar. Und wenn doch, wäre das für sich genommen
schon ein sehr interessantes Phänomen, dass dieselbe Variable in verschiedenen Gruppen ganz unterschiedlichen
Gesetzen folgt.

Durchführen kannst Du die Varianzanalyse ohne weiteres, aber wenn irgendwo die Messwerte extrem schief
verteilt sind, dann stellt sich die Frage, ob Mittelwerte tatsächlich überall gleich repräsentativ sind.

Könnte ich einfach alle Variablen logarithmieren (auch die, die es nicht bräuchten), um das einheitlich zu haben?

Wie schon gesagt, es geht hier nicht darum, in den Daten herumzufuhrwerken, um irgendwelche
Analysen hinzubiegen, auch nicht darum, ob Tabellen schön einheitlich aussehen, sondern um
substanzielle Fragen. Wenn für ein biologisches Phänomen eine exponentielle Verteilung
vorliegt, ist eine Transformation ja nichts ungewohntes. Wenn nicht, dann lässt man es bleiben.

Andererseits sehe ich erst jetzt, dass Du anscheinend mit Anteilswerten rechnest, nicht mit
Anzahl von Zellen. Ob da eine überhaupt Logarithmierung passend ist, weiß ich auf Anhieb
nicht. Sollte eigentlich aus Deiner Literatur hervorgehen, wie sie das dort handhaben.

Mit freundlichen Grüßen

PonderStibbons

[bele]

Hallo Elisabetha,

3000 Datensätze als Vergleich zu haben, ist eine bequeme Situation. Aus aber nur 97 + 67 + 25 Fällen tiefere Erkenntnisse über 25 verschiedene FACS-Parameter gewinnen zu wollen ist dann doch eher sportlich.

Worum geht es denn bei der Arbeit letzten Endes? Geht es darum, dass man aus dem FACS der BAL das Risiko für das Vorliegen dieser drei Krankheiten abschätzen möchte? Oder geht es darum, die Zellzusammensetzung bei diesen Krankheiten besser zu verstehen, um die Krankheiten besser zu verstehen? Vielleicht gibt es ja noch andere Ansätze als t-Test und ANOVA.

LG,
Bernhard



PS: Was die Darstellung via Mittelwert und Median angeht: Es gibt keinen guten Grund, nicht für metrische jede Variable sowohl Mittelwert als auch Median anzugeben. Das ist einfach nur eine weitere Spalte. Wenn Du willst, kannst Du sogar noch eine weitere Spalte für die Schiefe einführen. Dann ist das Thema endgültig vom Tisch.

[Elisabeta]

Hallo Bernhard,

ja, es geht eher darum, wie die Zellzusammensetzungen in den Krankheitsgruppen sind, ob es bestimmte Korrelationen gibt.
Ein Risiko möchte ich nicht abschätzen.
Und stimmt, noch mehr als den Mittelwert und die Standardabweichung anzugeben, ist eigentlich kein Problem : )

Vielen Dank für die Hilfe!

[Elisabeta]

Hallo PonderStibbons,

das Logarithmieren macht bei den durchflusszytometrisch erhobenen Parametern Sinn, ist auch mit der betreuenden Mitarbeiterin im Labor so besprochen.

Wo kann ich deine hilfreichen Aussagen zu den Voraussetzungen und Verletzung der Voraussetzungen der Varianzanalyse nochmal in Ruhe nachlesen?

Danke !