Eine Zufallsvariable X sei normalverteilt mit Erwartungswert 250 und Varianz 55. Es wird eine einfache Zufallsstichprobe X1,X2,…,X15 vom Umfang n=15 gezogen und der Stichprobenmittelwert X-Dach berechnet.
a) Bestimmen Sie den Erwartungswert des Stichprobenmittels X-Dach
E[X-Dach] =
b) Bestimmen Sie die Varianz des Stichprobenmittelwerts X-Dach. Geben Sie dieses Ergebnis kaufmännisch auf zwei Nachkommastellen gerundet an.
V[X-Dach] =
c) Wie groß ist die Wahrscheinlichkeit, dass X-Dach größer als 253 ist? Runden Sie Ihr Ergebnis kaufmännisch auf vier Nachkommastellen.
P(X-Dach>253) =
d) Berechnen Sie das 0,01-Quantil und das 0,99-Quantil von X-Dach. Runden Sie Ihre Ergebnisse kaufmännisch auf zwei Nachkommastellen.
x0,99 =
x0,01 =
Dies ist meine erste Frage hier, da ich nicht weiter komme.. Hoffe ich darf diese so formfrei hier stellen, ansonsten seht es mir bitte nach und weißt mich auf Anpassungen hin.
Danke vorab!
Diverse Werte eine normalverteilten Zufallsvariable bestimme
Thema bewerten: 




 • 9 Beiträge
• Seite 1 von 1
• 9 Beiträge
• Seite 1 von 1
- Gast1996
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 25. Jun 2018, 14:17
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Hi,
- welches Lehrbuch benutzt Du?
Gruß
S.
- welches Lehrbuch benutzt Du?
Gruß
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4369
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Hi,
ich benutze das Lehrbuch von F.Kronthaler Statistik angewandt.
Gruß
ich benutze das Lehrbuch von F.Kronthaler Statistik angewandt.
Gruß
- Gast1996
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 25. Jun 2018, 14:17
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Lies mal unter "Hausaufgaben" in nutzung-des-forums-f44/das-musste-mal-gepostet-werden-t6682.html
Übrigens haben wir hier im Forum die Möglichkeit, zu verwenden. Damit wird aus X-Dach dann einfach
zu verwenden. Damit wird aus X-Dach dann einfach 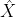
und aus V[X-Dach] wird) , was sich einfacher liest.
, was sich einfacher liest.
LG,
Bernhard
PS: Weißt Du, was ein Standardfehler ist?
Übrigens haben wir hier im Forum die Möglichkeit,
und aus V[X-Dach] wird
LG,
Bernhard
PS: Weißt Du, was ein Standardfehler ist?
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Okay danke für die Information, ist allerdings keine Hausaufgabe sondern eine Lernübung für anstehende Klausuren bei denen ich schlichtweg nicht voran kommen.
Ein Standardfehler ist die Standardabweichung der Stichprobenverteilung einer Stichprobenfunktion.
Ein Standardfehler ist die Standardabweichung der Stichprobenverteilung einer Stichprobenfunktion.
- Gast1996
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 25. Jun 2018, 14:17
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Sehe ich als äquivalent zu Hausaufgaben an.
Zu Aufgabe a): Wenn , welchen Wert erwartest Du denn dann für
, welchen Wert erwartest Du denn dann für 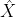 ? Der Wert, den Du da erwartest ist der Erwartungswert.
? Der Wert, den Du da erwartest ist der Erwartungswert.
Wenn ein Standardabweichung sowas ähnliches wie eine Varianz ist, und immer 15 Elemente ziehen und mitteln eine Stichprobenfunktion ist, dann hilft so ein Standardfehler vielleicht, "die Varianz des Stichprobenmittelwerts" zu bestimmen? Das würde uns für Aufgabe b) echt helfen.
LG,
Bernhard
Zu Aufgabe a): Wenn
Gast1996 hat geschrieben:Ein Standardfehler ist die Standardabweichung der Stichprobenverteilung einer Stichprobenfunktion.
Wenn ein Standardabweichung sowas ähnliches wie eine Varianz ist, und immer 15 Elemente ziehen und mitteln eine Stichprobenfunktion ist, dann hilft so ein Standardfehler vielleicht, "die Varianz des Stichprobenmittelwerts" zu bestimmen? Das würde uns für Aufgabe b) echt helfen.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Das hilft mir alles nicht wirklich weiter, bin bei dem Thema nicht wirklich sicher.
Trotzdem danke, werde mich mit Kommilitonen hinsetzen..
Trotzdem danke, werde mich mit Kommilitonen hinsetzen..
- Gast1996
- Grünschnabel

- Beiträge: 4
- Registriert: Mo 25. Jun 2018, 14:17
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Tja, das ist immer etwas blöd, weil unsereins ja nicht weiß, was man voraussetzen darf und wo es klemmt und Du uns diesbezüglich ja auch keine Hinweise geben konntest. Begriffe wie "Erwartungswert" erklären sprengt sicher den Rahmen eines Forumsposts. Viel Glück.
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Diverse Werte eine normalverteilten Zufallsvariable best
Hi,
Du brauchst nur deine wenigen Zahlen in einfache Formeln (deines Buches?) einzusetzen.
Gruß
S.
Du brauchst nur deine wenigen Zahlen in einfache Formeln (deines Buches?) einzusetzen.
Gruß
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4369
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Thema bewerten: 




 • 9 Beiträge
• Seite 1 von 1
• 9 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 8 Gäste


