Hallo zusammen
ich habe eine Frage zur logistischen Regression. Und zwar habe ich ein abhängigee Variable, die in vier verschiedenen Bundesländern (A, B, C, D) gemessen wurde. Daneben gibt es zahlreiche erklärende Merkmale - darunter eben auch die Variable "Bundesland" welche 4 Ausprägungen hat.
Wenn ich die Bundesland-Variable nun als aV in das Modell aufnehme, wird sie dummy-codiert, d.h. es wird eine Referenz-Kategorie angenommen (z.B. Bundesland A). Für die drei übrigen Merkmalsausprägungen (B, C, D) wird dann der Korrelationsoeffizient berechnet. D.h. ich erhalte nur Regressionskoeffizienten für die Länder B, C und D. Der OR (e^B) gibt dann an, zu welchem Faktor sich die jeweilige Kategorie von der Referenzkategorie unterscheidet.
Nun gibt es für mich aber inhaltlich überhaupt keinen Grund, weshalb ich ausgerechnet ein bestimmtes Bundesland als Referenzkategorie angeben sollte, vielmehr sind alle Länder gleichwertig. Wäre es hier nicht besser, wenn man stattdessen einfach vier (!) dichotome Merkmale, eine für jedes Bundesland, in das Modell aufnimmt? Was mich interessiert ist eben nicht unbedingt unbedingt ein Vergleich eines Landes (z.B. B) mit der Referenzkategorie (A), sondern, ein Vergleich eines Landes mit den übrigen drei Ländern.
Dass man bei der Dummy-Codierung einer nominalen Variablen mit k Ausprägungen nur k-1 Variablen erstellen sollte, ist mir schon klar (Multikollinearität, kein zusätzlicher Informationsgewinn der letzten Variable etc.).
Vielen Dank für eure Antworten!
Dummy-Codierung bei der logistischen Regression
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
- integral
- Power-User

- Beiträge: 57
- Registriert: Fr 17. Jun 2011, 10:08
- Danke gegeben: 4
- Danke bekommen: 2 mal in 2 Posts
Re: Dummy-Codierung bei der logistischen Regression
integral hat geschrieben:Wäre es hier nicht besser, wenn man stattdessen einfach vier (!) dichotome Merkmale, eine für jedes Bundesland, in das Modell aufnimmt? Was mich interessiert ist eben nicht unbedingt unbedingt ein Vergleich eines Landes (z.B. B) mit der Referenzkategorie (A), sondern, ein Vergleich eines Landes mit den übrigen drei Ländern.
Ich habe noch nicht ganz verstanden, warum Du das besser findest. Rein technisch kann es funktionieren, wenn Du ein Modell ohne Intercept/y-Achsenabschnitt im linearen Teil rechnen lässt.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Dummy-Codierung bei der logistischen Regression
bele hat geschrieben:Ich habe noch nicht ganz verstanden, warum Du das besser findest. Rein technisch kann es funktionieren, wenn Du ein Modell ohne Intercept/y-Achsenabschnitt im linearen Teil rechnen lässt.
Mein Problem ist folgendes: Bei den Ergebnissen bekomme ich dann die Regressionskoeffizienten für die Länder B, C und D angezeigt (vorausgesetzt A wäre die Referenzkategorie). Damit kann ich zwar das OR berechnen,
indem ich den Koeffizienten exponenziere, aber inhaltlich würde mir ein OR von beispielsweise 2 ja nur sagen, dass die Wahrscheinlichkeit für den Erfolgseintritt von B gegenüber A doppelt so hoch ist.
Was mich aber interessiert, ist eben nicht unbedingt der Vergleich zwischen Land A und Land B, sondern der "Einfluss" jedes einzelnen Landes. Das wäre ja dann gewissermassen ein Vergleich zwischen Land A mit den anderen drei Ländern zusammen. Es geht mir also weniger darum, ein möglichst gutes Gesamtmodell zu erhalten als vielmehr darum, die Einflüsse der einzelnen unabhängigen Variablen zu beurteilen.
Es ist für mich zudem auch nicht ganz logisch, wie ich die Ausgabe interpretieren soll. Warum sollte ich nur die Kombinationen A-B, A-C und A-D betrachten, nicht aber B-C, B-D und C-D ?
Ich hoffe, ich konnte mich verständlich ausdrücken.
LG, David
- integral
- Power-User

- Beiträge: 57
- Registriert: Fr 17. Jun 2011, 10:08
- Danke gegeben: 4
- Danke bekommen: 2 mal in 2 Posts
Re: Dummy-Codierung bei der logistischen Regression
Hi,
- N?
- Wie sieht Dein Modell konkret aus und wie rechnest Du das?
- Das hängt von Deinem Thema (von der Fragestellung) ab
- Die Umsetzung hängt von Deiner Software ab.
Gruß
S.
Warum sollte ich nur die Kombinationen A-B, A-C und A-D betrachten, nicht aber B-C, B-D und C-D ?
- N?
- Wie sieht Dein Modell konkret aus und wie rechnest Du das?
Warum sollte ich nur die Kombinationen A-B, A-C und A-D betrachten, nicht aber B-C, B-D und C-D ?
- Das hängt von Deinem Thema (von der Fragestellung) ab
- Die Umsetzung hängt von Deiner Software ab.
Gruß
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4361
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Dummy-Codierung bei der logistischen Regression
Also ich habe hier einmal ein einfaches Testmodell zu Anschauungszwecken erstellt, weil ich die Originaldaten nicht hier reinstellen darf. Die Fallzahl im richtigen Datensatz beträgt ca. n=4000. Die abhängige Variable Y ist dichotom und es gibt drei unabhängige Variablen (country, var1 und var2), von denen die letzten beiden kontinuierlich sind und die erste nominal mit den Kategorien (A, B, C und D).
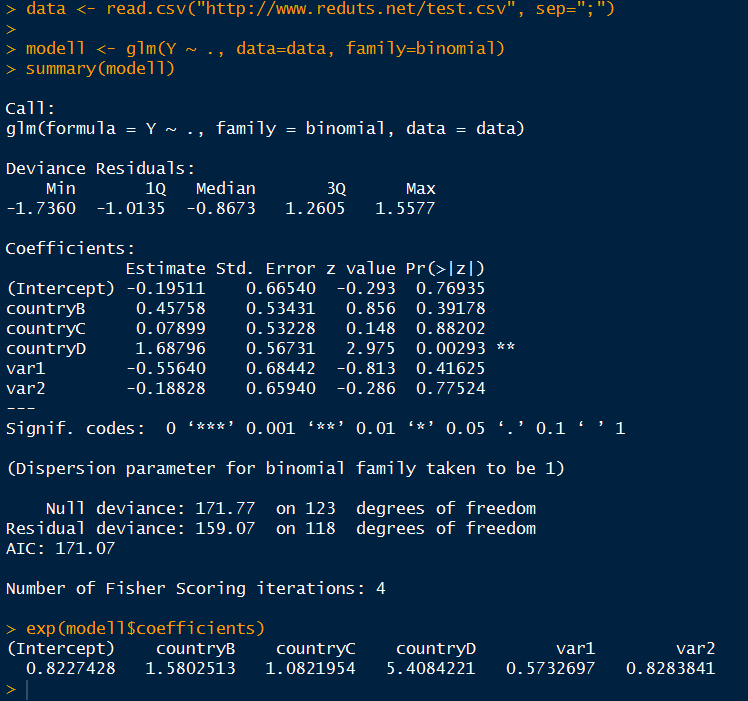
Die Software gibt mir nun an, dass sich Land D hinsichtlich der abhängigen Variable signifikant von Land A unterscheidet (Land A wird von "R" automatisch als Referenzkategorie angenommen.).
Wenn man sich die OR, d.h. die exponenzierten Regressionskoeffizienten, anschaut, kann man sagen, dass die Wahrscheinlichkeit für die Zielgrösse in Land D um den Faktor 5.408 grösser ist als in Land A.
Mein Unverständnis liegt nun aber darin, dass mich diese Angabe gar nicht interessiert. Was ich wirklich wissen möchte ist, um welchen Faktor sich die Wahrscheinlichkeit für die Zielgrösse erhöht, wenn man z.B. im Land A wohnt.
Oder habe ich das falsch interpretiert und die Regressionskoeffizienten beziehen sich gar nicht auf den Vergleich zum Land A (B vs. A, C vs. A, D. vs. A) sondern auf den Vergleich (B vs. Nicht-B; C vs. Nicht-C; D vs. Nicht-D)?
Falls letzteres der Fall wäre, hätte ich einfach das Problem, dass der Vergleich A vs. Nicht-A gar nicht ausgegeben wird.

Die Software gibt mir nun an, dass sich Land D hinsichtlich der abhängigen Variable signifikant von Land A unterscheidet (Land A wird von "R" automatisch als Referenzkategorie angenommen.).
Wenn man sich die OR, d.h. die exponenzierten Regressionskoeffizienten, anschaut, kann man sagen, dass die Wahrscheinlichkeit für die Zielgrösse in Land D um den Faktor 5.408 grösser ist als in Land A.
Mein Unverständnis liegt nun aber darin, dass mich diese Angabe gar nicht interessiert. Was ich wirklich wissen möchte ist, um welchen Faktor sich die Wahrscheinlichkeit für die Zielgrösse erhöht, wenn man z.B. im Land A wohnt.
Oder habe ich das falsch interpretiert und die Regressionskoeffizienten beziehen sich gar nicht auf den Vergleich zum Land A (B vs. A, C vs. A, D. vs. A) sondern auf den Vergleich (B vs. Nicht-B; C vs. Nicht-C; D vs. Nicht-D)?
Falls letzteres der Fall wäre, hätte ich einfach das Problem, dass der Vergleich A vs. Nicht-A gar nicht ausgegeben wird.
- integral
- Power-User

- Beiträge: 57
- Registriert: Fr 17. Jun 2011, 10:08
- Danke gegeben: 4
- Danke bekommen: 2 mal in 2 Posts
Re: Dummy-Codierung bei der logistischen Regression
R-Testmodelle besser hier:
http://www.r-forum.de/
http://www.r-forum.de/
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4361
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Dummy-Codierung bei der logistischen Regression
@integral Du benutzt R. Es gibt keinen Grund, Screenshots zu machen. Du kannstdie Ausgabe von R einfach mit der Maus markieren und per copy&paste hier in code-Tags posten.
Bleiben wir zunächst im linearen Teil des Modells: Der Unterschied zwischen A und B beträgt 0,489 logits. Der Unterschied zwischen A und D beträgt 1,690 logits. Also beträgt der Unterschied zwischen B und D 1,690 - 0,489 logits also 1,204 logits.
Der Vergleich zwischen B und D ist also aufgrund Deiner Rechnung bereits jetzt möglich. Was so einfach nicht zu übertragen ist, ist die Signifikanz dieses Unterschieds. Der einfachste Weg, die zu testen, ist dass Du dasselbe Modell nochmal mit B oder mit D als Basiskategorie rechnest. Siehe dazu
Vorläufig halte ich das hier noch für eine Statistik-Frage, die in diesem Forum richtig aufgehoben ist. Wenn es im Verlauf zu einer R-Frage wird, dann halte ich das andere deutschsprachige R-Forum für besser als das von strukturmarionette verlinkte.
LG,
Bernhard
Bleiben wir zunächst im linearen Teil des Modells: Der Unterschied zwischen A und B beträgt 0,489 logits. Der Unterschied zwischen A und D beträgt 1,690 logits. Also beträgt der Unterschied zwischen B und D 1,690 - 0,489 logits also 1,204 logits.
- Code: Alles auswählen
> exp(1.201)
[1] 3.323439
Der Vergleich zwischen B und D ist also aufgrund Deiner Rechnung bereits jetzt möglich. Was so einfach nicht zu übertragen ist, ist die Signifikanz dieses Unterschieds. Der einfachste Weg, die zu testen, ist dass Du dasselbe Modell nochmal mit B oder mit D als Basiskategorie rechnest. Siehe dazu
- Code: Alles auswählen
help("relevel")
Vorläufig halte ich das hier noch für eine Statistik-Frage, die in diesem Forum richtig aufgehoben ist. Wenn es im Verlauf zu einer R-Frage wird, dann halte ich das andere deutschsprachige R-Forum für besser als das von strukturmarionette verlinkte.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 0 Gäste


