bin in Statistik eher Anfänger und wollt mal fragen ob mir wer bei diesem Beispiel helfen kann!
Also ich hab folgende Angabe:
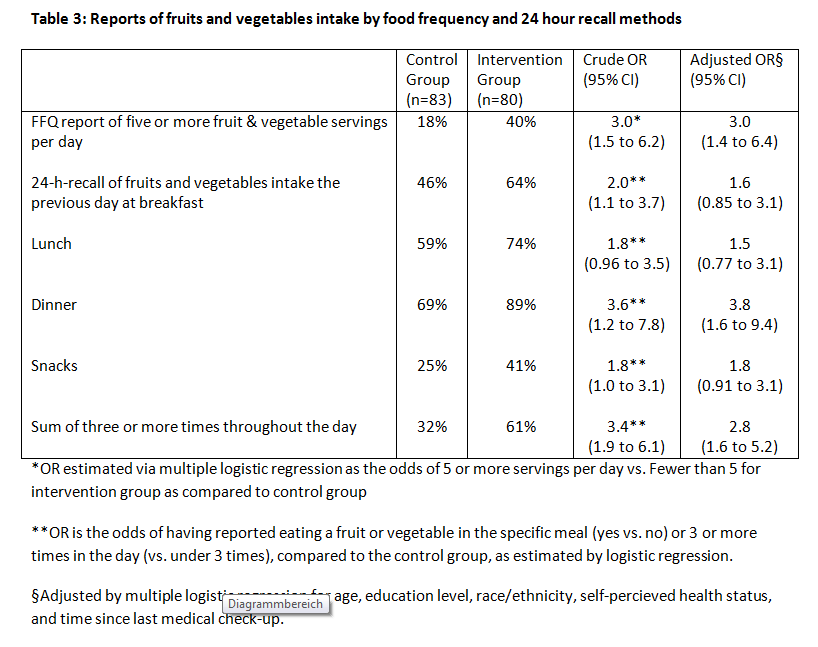
Die folgende Tabelle stammt von einem Artikel des Nutritional Journal. Es wurde der Obst- und Gemüsekonsum von 163 Personen erhoben, einerseits mittels eines Fragebogens (FFQ Report), andererseits telefonisch (24-h-recall). Es wurde zwischen zwei Gruppen verglichen („intervention group“ gegen „controll group), wobei es für diese Aufgabe nicht wesentlich ist zu wissen, worin die Intervention genau bestand.
Und hier nun die 2 Fragen:
1.) Gib die Formel für das logistische Regressionsmodell für die erste Zeile (FFQ report) und die dritte Spalte der Tabelle (Crude OR). Was ist die abhängige, was die unabhängige Variable? Wie ist Crude OR zu interpretieren, wie das zugehörige Konfidenzintervall? Unterscheidet sich die „intervention group“ signifkant von der „control group“?
Also wo ich mir grundsätzlich immer schwer tu! Was ist die abhängige und die unabhängige Variable. In diesem Fall würde ich FFQ als unabhängig und Crude OR als abhängige Variable (Zielvariable) einstufen. Das logistische Regressionsmodell habe ich mir zwar unter http://de.wikipedia.org/wiki/Logistische_Regression angesehen! Verstehe aber leider nur Bahnhof. Interpretation von nicht adjustierte OR und CI: Das Chancenverhältnis. Also die Interventionsgruppe konsumiert 3 x soviel Obst. Wobei was ist der Unterschied zwischen nicht adjustiert und adjustiert? Konfidenzintervall: Streuung. Statstistisch signifikant oder nicht???
2.) Wie lautet das verwendete logistische Regressionsmodell in Zeile 3 (lunch) und Spalte 4 (Adjusted OR). Nimm der Einfachheit halber an, dass sämtliche kategorielle Variablen, für die Adjusted wurde, sich jeweils durch eine einzige Dummyvariable beschreiben lassen. Wie ist hier das Konfidenzintervall der adjusted OR zu interpretieren? Unterscheidet sich die „intervention group“ signifikant von der „control group“?
Wie lautet das verwendete logistische Regressionsmodell?? Hier steig ich überhaupt aus?
Ich gebs zu das sind viele Fragen, aber mit ein paar Anregungen wäre mir schon geholfen!





