Hallo,
Da nun alle meine Daten zu meiner Dissertation vorliegen, habe ich mich daran gemacht statistisch signigikante Unterschiede in meinen Daten zu suchen. Es handelt sich um eine 6x8 Kreuztabelle, in der die chemische Zusammenstzung von Partikeln, die in 6 verschiedene Gruppen eingeteilt wurden (relative Häufigkeit in % der verschiedenen Gruppen), nach 8 verscheidenen Windrichtungen betrachtet werden (siehe Talle im Anhang).
Da es sich hier um nominal skalierte Daten handelt habe ich eine Chi-Quadrat-Test durchgeführt. Die Frage war, ob es statistisch signifikante Unterschiede der chemischen Zusammensetzung in den Windrichtungen gibt.
Der Chi-Quadrat-Test liefert mir einen P-Wert von 2,5e-54. Bei einem angenommen Signifikanzniveau von 95% bedeutet dies also, daß es statistisch signifikante Unterscheide der chemischen Zusammensetzung in den Windrichtungen gibt. Das war allerdings auch nicht wirklich überraschend.
Was mich allerdings wirklich interessiert ist, wo diese Unterschiede liegen. Also welche Windrichtung leigt denn hier am weitesten daneben, oder anders gefragt: Kann man Anhand statistischer Kriterien die Windrichtungen in irgendeiner Art und Weise Gruppieren, sodaß man beispielsweise sagen kann. Ost, West und Nordwest sind statistisch gesehen gleich, unterscheiden sich aber signifikant von Südost und Nord, die wiederum verschieden von den restlichen sind.
Gibt es da statistische Mittel die einen so eine Aussgae treffen lassen.
Leider konnte ich keine Beispiele o.Ä. in der gängigen Literatur finden. Und mein Chef, sonst ein statistik Ass meinte, daß er das Problem nur mit metrisch skalierten Daten bei einer Varianzanalyse kennen würde. Ich suche da also sowas wie ein Analogon für den Chi-Quadrat-Test.
Ich hoffe mal auf Input von eurer Seite und danke schonmal fürs Durchlesen
Thomas
Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
- Dateianhänge
-
- Kreuztabelle
- Tabelle1.jpeg (73.53 KiB) 3659-mal betrachtet
- hogohogo
- Grünschnabel

- Beiträge: 6
- Registriert: Di 6. Mär 2012, 23:01
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
hogohogo hat geschrieben:Hallo,
Bei einem angenommen Signifikanzniveau von 95% bedeutet dies....
Thomas
Das Signifikanzniveau, welches du hier annimmst ist nicht 1-alpha, sondern alpha=0.05.
hogohogo hat geschrieben:Hallo,
Kann man Anhand statistischer Kriterien die Windrichtungen in irgendeiner Art und Weise Gruppieren, sodaß man beispielsweise sagen kann. Ost, West und Nordwest sind statistisch gesehen gleich, unterscheiden sich aber signifikant von Südost und Nord, die wiederum verschieden von den restlichen sind.
Gibt es da statistische Mittel die einen so eine Aussgae treffen lassen.
Thomas
Stichwort Clusteranalyse, welches ein exploratives Verfahren ist um potentielle Gruppen zu entdecken. Hier gibt es Verfahren für welche das zugrunde liegende Merkmal nicht metrisch skaliert sein muss. So wie ich das sehe ist dein zugrunde liegendes Merkmal aber eigentlich metrisch (gemessene Menge Partikel eines bestimmten Typs in einem bestimmten Zeitraum). Liegen dir die Daten nur in dem obgen schon aggregierten Zustand vor? Falls nicht gehen dir unter Umständen schon einige Informationen verloren.
Bei der Clusteranalyse musst du allerdings bedenken, dass du zwar Gruppen erhälst aber keine Information darüber was genau diese Gruppen unterscheidet. Zwar kannst du im nachhinein hoffen, dass die Gruppen, welche sich ergeben haben bestimmte abgrenzbare Eigenschaften besitzen. Dies ist jedoch nicht immer der Fall (bezieht sich auf jede gemessene Dimension).
Angenommen, dass sich sinnvolle Gruppen ergeben würden könntest du mit post hoc test überprüfen, welche Unterschiede sich genau ergeben.
Gruß
Druss
- Druss
- Power-User

- Beiträge: 92
- Registriert: Mo 29. Aug 2011, 14:20
- Danke gegeben: 0
- Danke bekommen: 10 mal in 10 Posts
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Hi,
Die Kategorien sind nominalskaliert. OK.
Aber warum sollten die Orig-Messwerte (in ´Partikeln´, KG oder Volumeneinheiten) nicht als metrisch /intervallskaliert aufgefasst werden können?
S.
sonst ein statistik Ass meinte, daß er das Problem nur mit metrisch skalierten Daten bei einer Varianzanalyse kennen würde
Die Kategorien sind nominalskaliert. OK.
Aber warum sollten die Orig-Messwerte (in ´Partikeln´, KG oder Volumeneinheiten) nicht als metrisch /intervallskaliert aufgefasst werden können?
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4361
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Hallo,
vielen Dank schon Mal für die Anregungen.
Schon klar. Hab die Nomenklatur da nicht korrekt verwandt.
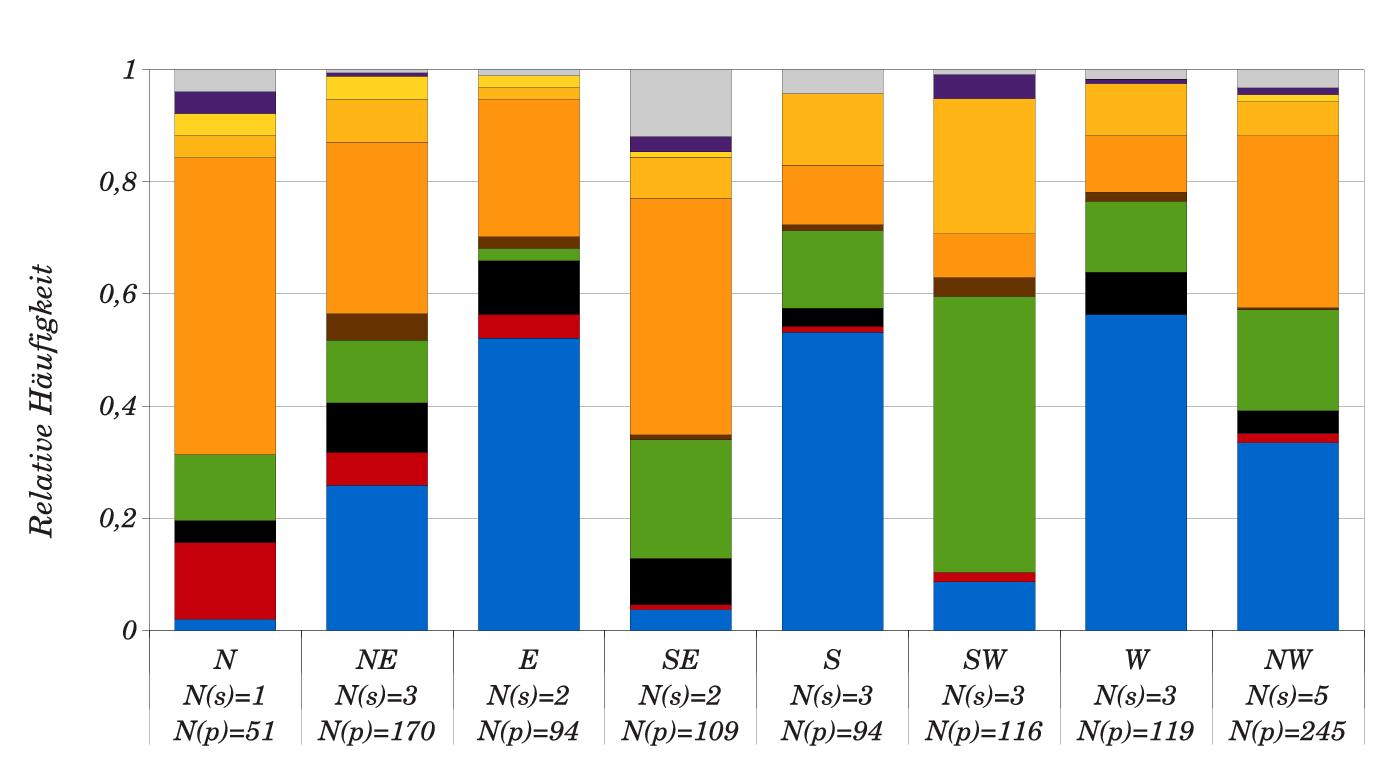
Es handelt sich um die relative Häufigkeit verschiedener Partikeltypen bei verschiedenen Windrichtungen. Hab nochmal die entsprechende Grafik drangehängt. Mit Zeit hat das alles nichts zu tun.
Zur Skalierung: Das Merkmal ist die je nach Windrichtung unterschiedliche relative Häfigkeit der Gruppen (das was in der ersten Zeile meiner Tabelle steht). Diese Gruppen sind doch nicht metrisch. Die heißen biologisch, Ruß usw.. Dabei gibt es keine Rangfolge. Die Windrichtungen könnte man zwar als ordinal auffassen, das möchte ich an dieser Stelle aber nicht, da ich noch ein ganz ähnliches Problem habe, bei dem die Daten nicht nach Windrichtungen sondern nach Trajektorien betrachtet werden (hier ganz klar wieder nominal).
Die Eingruppierung der Partikel in diese Gruppen erfolgte nach chemischen Kriterien quasi per Hand. Hierbei waren nicht nur die zahlenmäßig fassbare Zusammensetzung entscheidend sondern auch das Aussehen, die Morphologie, der Partikel. Und die Beurteilung des Aussehens kann mir kein statistischer Test abnehmen. Die Daten liegen also so vor wie sie sind. Der abgebildete Datensatz wurde allerdings für den Chi-Quadrat-Test leicht reduziert, soll heißen Partikelgruppen mit geringer Häfufigkeit wurden zusammengefaßt, um das Kriterium , daß keine erwartete Häufigkeit kleiner als 5 ist, zu erfüllen. Dieses Zusammenfassen wurde aber nach sinnvollen Kriterien gemacht, kann aber für einen anderen Test wieder rückgängig gemacht werden. Dann wären es halt 3 Partikelgrupen mehr.
Es geht bei der Frage nicht um eine neuerliche Gruppierung der Partikel nach chemischer Zusammensetzung (die ist bereits Erfolgt, und da wird nicht mehr dran gerüttelt), sondern um eine Gruppierung bzw. die Unterschiede der Windrichtungen in Abhängigkeit der relativen Zusammensetzung (d.h. der für jede Windrichtung unterschiedlichen oder nicht unterschiedlichen Zusammensetzung der Häufigkeiten in den verschiedenen Gruppen).
Mir reicht es aus zu wissen, das sich zwei oder mehr Windrichtungen in ihrer Zusammensetzung voneinander unterscheiden. Wo genau die Unterschiede liegen, also ob der Unterschied aus einer statistisch signifikanten Abweichung in einer bestimmten Partikelgruppe herrührt oder einer anderen bestimmten ist zweitrangig.
Gruß
Thomas
vielen Dank schon Mal für die Anregungen.
Das Signifikanzniveau, welches du hier annimmst ist nicht 1-alpha, sondern alpha=0.05.
Schon klar. Hab die Nomenklatur da nicht korrekt verwandt.
(gemessene Menge Partikel eines bestimmten Typs in einem bestimmten Zeitraum)
Es handelt sich um die relative Häufigkeit verschiedener Partikeltypen bei verschiedenen Windrichtungen. Hab nochmal die entsprechende Grafik drangehängt. Mit Zeit hat das alles nichts zu tun.
Zur Skalierung: Das Merkmal ist die je nach Windrichtung unterschiedliche relative Häfigkeit der Gruppen (das was in der ersten Zeile meiner Tabelle steht). Diese Gruppen sind doch nicht metrisch. Die heißen biologisch, Ruß usw.. Dabei gibt es keine Rangfolge. Die Windrichtungen könnte man zwar als ordinal auffassen, das möchte ich an dieser Stelle aber nicht, da ich noch ein ganz ähnliches Problem habe, bei dem die Daten nicht nach Windrichtungen sondern nach Trajektorien betrachtet werden (hier ganz klar wieder nominal).
Liegen dir die Daten nur in dem obgen schon aggregierten Zustand vor? Falls nicht gehen dir unter Umständen schon einige Informationen verloren.
Die Eingruppierung der Partikel in diese Gruppen erfolgte nach chemischen Kriterien quasi per Hand. Hierbei waren nicht nur die zahlenmäßig fassbare Zusammensetzung entscheidend sondern auch das Aussehen, die Morphologie, der Partikel. Und die Beurteilung des Aussehens kann mir kein statistischer Test abnehmen. Die Daten liegen also so vor wie sie sind. Der abgebildete Datensatz wurde allerdings für den Chi-Quadrat-Test leicht reduziert, soll heißen Partikelgruppen mit geringer Häfufigkeit wurden zusammengefaßt, um das Kriterium , daß keine erwartete Häufigkeit kleiner als 5 ist, zu erfüllen. Dieses Zusammenfassen wurde aber nach sinnvollen Kriterien gemacht, kann aber für einen anderen Test wieder rückgängig gemacht werden. Dann wären es halt 3 Partikelgrupen mehr.
Es geht bei der Frage nicht um eine neuerliche Gruppierung der Partikel nach chemischer Zusammensetzung (die ist bereits Erfolgt, und da wird nicht mehr dran gerüttelt), sondern um eine Gruppierung bzw. die Unterschiede der Windrichtungen in Abhängigkeit der relativen Zusammensetzung (d.h. der für jede Windrichtung unterschiedlichen oder nicht unterschiedlichen Zusammensetzung der Häufigkeiten in den verschiedenen Gruppen).
Bei der Clusteranalyse musst du allerdings bedenken, dass du zwar Gruppen erhälst aber keine Information darüber was genau diese Gruppen unterscheidet.
Mir reicht es aus zu wissen, das sich zwei oder mehr Windrichtungen in ihrer Zusammensetzung voneinander unterscheiden. Wo genau die Unterschiede liegen, also ob der Unterschied aus einer statistisch signifikanten Abweichung in einer bestimmten Partikelgruppe herrührt oder einer anderen bestimmten ist zweitrangig.
Gruß
Thomas
- hogohogo
- Grünschnabel

- Beiträge: 6
- Registriert: Di 6. Mär 2012, 23:01
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Hi,
Die H0 dieses Signifikanztestes lautet: Es besteht kein Zusammenhang zwischen den zwei (kategorialen) Variablen -oder- Die zwei Vars sind unabhängig voneinander.
(mehr nicht)
Wenn die Frage nach (konkreten) signifikanten Abweichung zwischen Einzelkategorien zweitragig ist, dann erübrigen sich weitere Überlegungen.
[was aber keinesfalls bedeutet,dass das nicht möglich wäre.]
Das ist ja bereits ersichtlich aus den deskriptiven ´Prozentuierungen´ der Grafiken ersichtlich.
S.
Der abgebildete Datensatz wurde allerdings für den Chi-Quadrat-Test leicht reduziert, soll heißen Partikelgruppen mit geringer Häfufigkeit wurden zusammengefaßt, um das Kriterium , daß keine erwartete Häufigkeit kleiner als 5 ist, zu erfüllen.
Die H0 dieses Signifikanztestes lautet: Es besteht kein Zusammenhang zwischen den zwei (kategorialen) Variablen -oder- Die zwei Vars sind unabhängig voneinander.
(mehr nicht)
Mir reicht es aus zu wissen, das sich zwei oder mehr Windrichtungen in ihrer Zusammensetzung voneinander unterscheiden. Wo genau die Unterschiede liegen, also ob der Unterschied aus einer statistisch signifikanten Abweichung in einer bestimmten Partikelgruppe herrührt oder einer anderen bestimmten ist zweitrangig.
Wenn die Frage nach (konkreten) signifikanten Abweichung zwischen Einzelkategorien zweitragig ist, dann erübrigen sich weitere Überlegungen.
[was aber keinesfalls bedeutet,dass das nicht möglich wäre.]
Mir reicht es aus zu wissen, das sich zwei oder mehr Windrichtungen in ihrer Zusammensetzung voneinander unterscheiden
Das ist ja bereits ersichtlich aus den deskriptiven ´Prozentuierungen´ der Grafiken ersichtlich.
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4361
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Hallo,
Das heißt was ?
Es geht doch darum, die augenscheinlichen Unterschiede durch einen statistischen Test zu untermauern.
NE und NW sind beispielsweise sehr ähnlich. Ist der Unterschied zwischen beiden signifikant oder nicht ?
Und was würde man da konkret machen ?
Ich habe das Gefühl, daß du hier gar kein Problem siehst. Bin ich hier vielleicht völlig falsch vorgegangen. Sollte ich das ganze vielleicht mit nicht mit den relativen Häufigkeiten sondern mit den absoluten Häufigkeiten durch führen. Die absoluten Patikelzahlen (N(p)) in den einzelnen Windrichtungen sind nämlich äußerst unterschiedlich. Hat das Einfluss auf die Signigikanz.
Gruß
Thomas
Die H0 dieses Signifikanztestes lautet: Es besteht kein Zusammenhang zwischen den zwei (kategorialen) Variablen -oder- Die zwei Vars sind unabhängig voneinander.
(mehr nicht)
Das heißt was ?
Das ist ja bereits ersichtlich aus den deskriptiven ´Prozentuierungen´ der Grafiken ersichtlich.
Es geht doch darum, die augenscheinlichen Unterschiede durch einen statistischen Test zu untermauern.
NE und NW sind beispielsweise sehr ähnlich. Ist der Unterschied zwischen beiden signifikant oder nicht ?
[was aber keinesfalls bedeutet,dass das nicht möglich wäre.]
Und was würde man da konkret machen ?
Ich habe das Gefühl, daß du hier gar kein Problem siehst. Bin ich hier vielleicht völlig falsch vorgegangen. Sollte ich das ganze vielleicht mit nicht mit den relativen Häufigkeiten sondern mit den absoluten Häufigkeiten durch führen. Die absoluten Patikelzahlen (N(p)) in den einzelnen Windrichtungen sind nämlich äußerst unterschiedlich. Hat das Einfluss auf die Signigikanz.
Gruß
Thomas
- hogohogo
- Grünschnabel

- Beiträge: 6
- Registriert: Di 6. Mär 2012, 23:01
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Hallo,
ich habe bei meiner Auswertung grade ein ähnliches (ich denke sogar das gleiche) Problem ^^
Möchte evtl. jemand auf die Fragen von Thomas antworten? Bitte?
ich habe bei meiner Auswertung grade ein ähnliches (ich denke sogar das gleiche) Problem ^^
Möchte evtl. jemand auf die Fragen von Thomas antworten? Bitte?
- Tomati
- Einmal-Poster

- Beiträge: 1
- Registriert: Sa 29. Sep 2012, 10:15
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Chi-Quadrat-Test: Was kommt danach ? 6x8 Kreuztabelle
Erfahrungsgemäß ist es weitaus besser, wenn Du Dein konkretes Problem
selber beschreibst und die sich daraus ergebenden konkreten Fragen.
Mit freundlichen Grüßen
P.
selber beschreibst und die sich daraus ergebenden konkreten Fragen.
Mit freundlichen Grüßen
P.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11372
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Zurück zu Kreuztabellen & Chi²
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 0 Gäste