Hallo zusammen,
ich habe Probleme bei der Methodenwahl für die Berechnung von Korrelationen/Signifikanztests, die ich nachfolgend anhand eines Beispiels beschreibe:
angenommen ich betreibe eine Webseite, bei der sich die User mit einem Klick auf einen Butten einen Gutschein zuschicken lassen können. Jeder Klick auf den Button löst einen Prozess auf der Webseite aus, dessen Bearbeitung mehrere Sekunden dauert und am Ende dazu führt, dass dem User der Gutschein zugeschickt wird. Mich interessiert jetzt, ob es einen Zusammenhang zwischen der Anzahl der Klicks und der Dauer der Prozessbearbeitung gibt und wenn ja, welche Richtung dieser Zusammenhang hat. Als Datengrundlage stehen mir dafür die Anzahl der Klicks pro Stunde sowie die durchschnittliche Verarbeitungsgeschwindigkeit pro Klick in Sekunden für die letzten 24h zur Verfügung:
h Zeit Klicks
1 3,814 53
2 3,890 15
3 3,901 37
4 3,945 11
5 3,969 221
6 4,037 38
7 4,138 217
8 4,252 200
9 4,316 249
10 4,320 292
11 4,352 250
12 4,392 242
13 4,413 237
14 4,516 269
15 4,518 264
16 4,525 265
17 4,530 66
18 4,536 184
19 4,551 267
20 4,591 126
21 4,683 244
22 4,691 283
23 4,716 69
24 4,824 275
Bei Betrachtung der Daten zeigt sich, dass die Verarbeitungszeit zwar normalverteilt ist aber nicht die Anzahl der Klicks. Um den Zusammenhang zu untersuchen, habe ich deshalb den Spearman-Korrelationskoeffizienten berechnet.
Ich stehe gerade vor dem Problem, dass ich nicht genau weiß, welchen Signifikanztest ich verwenden soll. Aktuell benutze ich den t-test aber da der ja eigentlich eine Normalverteilung voraussetzt, diese bei der Anzahl der Klicks aber nicht gegeben ist, will ich ein passenderes Verfahren verwenden (auch wenn der t-test robust auf Verletzung der Normalverteilungsanforderung reagieren soll) . Hier fiel mein Blick auf den Mann-Whitney-U-Test. Hier habe ich aber zweierlei Schwierigkeiten:
1. In den Beispielen, die ich bisher zum Test gesehen habe, war immer mindestens eine Variable nominal- oder ordinalskaliert, was dann beim Bilden der Ränge dazu geführt hat, dass diese Variable "ignoriert" und die Rangbildung anhand der anderen intervallskalierten Variablen erfolgt ist. Wie mache ich das, wenn ich zwei metrische Variablen wie in meinem Beispiel habe?
2. Ich bin mir nicht sicher, ob die Anwendung des Mann-Whitney-U-Test überhaupt korrekt wäre, weil dieser ja für den Vergleich von zwei unabhängigen Stichproben gedacht ist. Ich bin mir bei meinen Daten um ehrlich zu sein nicht sicher, was genau hier als Stichprobe zu betrachten ist.
Kann mir bitte jemand weiterhelfen?
Grüße
Zusammenhang zwischen Prozessgeschwindigkeit und -objekten
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
Zusammenhang zwischen Prozessgeschwindigkeit und -objekten
Zuletzt geändert von Thymos2k am Do 4. Feb 2021, 18:39, insgesamt 1-mal geändert.
- Thymos2k
- Grünschnabel

- Beiträge: 4
- Registriert: Do 4. Feb 2021, 16:38
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Zusammenhang zwischen Prozessgeschwindigkeit und -objekt
Ich weiß nicht recht, was ein Signifikanztest hier bringen soll, aber ich würde erstmal ein Streudiagramm
machen und eine einfache lineare Regression von Geschwindigkeit auf Clicks rechnen (das ist übrigens
analog zu einer Korrelation). Falls n > 30, sind die Verteilungseigenschaften für den Signifikanztest bei
der Regression unerheblich. Allerdings weiß ich nicht, ob eine oder beide Variablen sehr schief verteilt
sein könnten (also mal 2 Histogramme anfertigen) und/oder ob die Beziehung erkennbar nichtlinear ist
(darum das Streudiagramm).
Mit freundlichen Grüßen
PonderStibbons
machen und eine einfache lineare Regression von Geschwindigkeit auf Clicks rechnen (das ist übrigens
analog zu einer Korrelation). Falls n > 30, sind die Verteilungseigenschaften für den Signifikanztest bei
der Regression unerheblich. Allerdings weiß ich nicht, ob eine oder beide Variablen sehr schief verteilt
sein könnten (also mal 2 Histogramme anfertigen) und/oder ob die Beziehung erkennbar nichtlinear ist
(darum das Streudiagramm).
Mit freundlichen Grüßen
PonderStibbons
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11372
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: Zusammenhang zwischen Prozessgeschwindigkeit und -objekt
Mit Blick auf die Beispieldaten: Es gibt 24 Datenpaare und bei visueller Prüfung erscheint die Variable Klicks bimodal verteilt. Die Frage lautet, wird der Server langsamer (die Reaktionszeit länger) wenn die Last grüßer wird (Klicks steigen). Das ist eine passende Fragestellung für eine Spearman-Korrelation und da die eine Rangtransformation durchführt stellt sich die Verteilungsannahme nicht mehr. Das Ergebnis ist erfreulich eindeutig:
Wenn man ein lineares Modell macht sind die Residuen sehr schön normalverteilt und als Regressiongleichung kommt heraus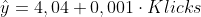
LG,
Bernhard
PS: hier die Dateneingabe, passende Grafiken und Korrelation in R:
- Code: Alles auswählen
> cor.test(klicks$Klicks, klicks$Zeit, method = "spearman")
Spearman's rank correlation rho
data: klicks$Klicks and klicks$Zeit
S = 1094, p-value = 0.009413
alternative hypothesis: true rho is not equal to 0
sample estimates:
rho
0.5243478
Wenn man ein lineares Modell macht sind die Residuen sehr schön normalverteilt und als Regressiongleichung kommt heraus
LG,
Bernhard
PS: hier die Dateneingabe, passende Grafiken und Korrelation in R:
- Code: Alles auswählen
klicks <- read.table(header = TRUE, dec = ",", text="h Zeit Klicks
1 3,814 53.000
2 3,890 15.000
3 3,901 37.000
4 3,945 11.000
5 3,969 221.000
6 4,037 38.000
7 4,138 217.000
8 4,252 200.000
9 4,316 249.000
10 4,320 292.000
11 4,352 250.000
12 4,392 242.000
13 4,413 237.000
14 4,516 269.000
15 4,518 264.000
16 4,525 265.000
17 4,530 66.000
18 4,536 184.000
19 4,551 267.000
20 4,591 126.000
21 4,683 244.000
22 4,691 283.000
23 4,716 69.000
24 4,824 275.000")
klicks$Klicks <- as.numeric(klicks$Klicks)
plot(klicks$Zeit ~ klicks$Klicks, xlab = "Klicks", ylab = "Zeit")
hist(klicks$Klicks, probability = TRUE, xlab = "Klicks", main = "")
lines(density(klicks$Klicks))
rug(x = klicks$Klicks)
cor.test(klicks$Klicks, klicks$Zeit, method = "spearman")
linear <- lm(klicks$Zeit ~ klicks$Klicks)
plot(linear) # Residuenanalyse
summary(linear)
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Zusammenhang zwischen Prozessgeschwindigkeit und -objekt
Hallo zusammen,
danke für die Rückmeldungen. Ich dachte, dass ein Signifikanztest hier nötig ist, um überhaupt davon ausgehen zu können, dass der Zusammenhang, den ich anhand des Spearmankoeffizienten berechne, mit hoher Wahrscheinlichkeit auch tatsächlich vorliegt.
@Bernhard:
Danke für deine Berechnungen. Kannst du mir sagen, welchen Signifikanztest R verwendet? Außerdem ist mir leider ein Formatierungsfehler bei den Klicks unterlaufen. Der Punkt müsste eigentlich ein Komma sein, sodass der erste Wert nicht 53000, sondern nur 53 Klicks ergibt. Könntest du das bitte nochmal mit R berechnen? Ich habe es weiter oben mal korrigiert.
Vielen Dank und Grüße
danke für die Rückmeldungen. Ich dachte, dass ein Signifikanztest hier nötig ist, um überhaupt davon ausgehen zu können, dass der Zusammenhang, den ich anhand des Spearmankoeffizienten berechne, mit hoher Wahrscheinlichkeit auch tatsächlich vorliegt.
@Bernhard:
Danke für deine Berechnungen. Kannst du mir sagen, welchen Signifikanztest R verwendet? Außerdem ist mir leider ein Formatierungsfehler bei den Klicks unterlaufen. Der Punkt müsste eigentlich ein Komma sein, sodass der erste Wert nicht 53000, sondern nur 53 Klicks ergibt. Könntest du das bitte nochmal mit R berechnen? Ich habe es weiter oben mal korrigiert.
Vielen Dank und Grüße
Zuletzt geändert von Thymos2k am Do 4. Feb 2021, 18:41, insgesamt 1-mal geändert.
- Thymos2k
- Grünschnabel

- Beiträge: 4
- Registriert: Do 4. Feb 2021, 16:38
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Zusammenhang zwischen Prozessgeschwindigkeit und -objekt
Achso und um noch etwas Hintergrundinformation zu geben: Ich habe vor diese Berechnungen automatisiert auf einer MSSQL-Datenbank auszuführen, weshalb visuelle Prüfverfahren etc. nicht angewandt werden können.
- Thymos2k
- Grünschnabel

- Beiträge: 4
- Registriert: Do 4. Feb 2021, 16:38
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Zusammenhang zwischen Prozessgeschwindigkeit und -objekt
Hallo Thymos,
Der Hilfetext von R schreibt:
und zitiert dazu
Ich hatte `exact` nicht gesetzt, sodass es hier NULL und nicht TRUE war, weshalb ich denke, dass diese Zahlen aus der asymptotischen t Approximation stammen.
Ich hatte Komma und Punkt beide als Dezimalzeichen interpretiert, deshalb bleibt es bei den o. g. Ergebnissen.
Wenn Du Dir R von www.r-project.org herunterlädst und meinen Code dorthin copypastest siehst Du auch an den Achsen der Grafiken, dass die Zahlen richtig interpretiert wurden. Im übrigen sind lineare Transformationen wie das Malnehmen oder Teilen mit/durch 1000 für Korrelationsmaße irrelevant.
LG,
Bernhard
Thymos2k hat geschrieben: Kannst du mir sagen, welchen Signifikanztest R verwendet?
Der Hilfetext von R schreibt:
For Spearman's test, p-values are computed using algorithm AS 89 for n < 1290 and exact = TRUE, otherwise via the asymptotic t approximation. Note that these are ‘exact’ for n < 10, and use an Edgeworth series approximation for larger sample sizes (the cutoff has been changed from the original paper).
und zitiert dazu
D. J. Best & D. E. Roberts (1975). Algorithm AS 89: The Upper Tail Probabilities of Spearman's rho. Applied Statistics, 24, 377–379. doi: 10.2307/2347111.
Myles Hollander & Douglas A. Wolfe (1973), Nonparametric Statistical Methods. New York: John Wiley & Sons. Pages 185–194 (Kendall and Spearman tests).
Ich hatte `exact` nicht gesetzt, sodass es hier NULL und nicht TRUE war, weshalb ich denke, dass diese Zahlen aus der asymptotischen t Approximation stammen.
Außerdem ist mir leider ein Formatierungsfehler bei den Klicks unterlaufen. Der Punkt müsste eigentlich ein Komma sein, sodass der erste Wert nicht 53000, sondern nur 53 Klicks ergibt.
Ich hatte Komma und Punkt beide als Dezimalzeichen interpretiert, deshalb bleibt es bei den o. g. Ergebnissen.
Wenn Du Dir R von www.r-project.org herunterlädst und meinen Code dorthin copypastest siehst Du auch an den Achsen der Grafiken, dass die Zahlen richtig interpretiert wurden. Im übrigen sind lineare Transformationen wie das Malnehmen oder Teilen mit/durch 1000 für Korrelationsmaße irrelevant.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Zusammenhang zwischen Prozessgeschwindigkeit und -objekt
Vielen Dank für deine Mühen Bernhard. Ich werde mir den AS 89 mal genauer anschauen.
- Thymos2k
- Grünschnabel

- Beiträge: 4
- Registriert: Do 4. Feb 2021, 16:38
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 0 Gäste


