Hallo liebe Forum-User,
ich würde gerne Beweisen, dass Häufigkeiten einer anderen Studie mit den Häufigkeiten meiner Studie übereinstimmen. Mir kam als erstes der Chi-Quadrat-Test in den Sinn. Jedoch will man mit diesem die Null-Hypothese mit einem Signifikanz-Niveau von <0,05 verwerfen, um zu beweisen, dass ein Unterschied in den Häufigkeiten besteht. Kann man diese Teststatistik trotzdem anwenden? Muss man das Signifikanz-Niveau ändern?
Bsp.: Andere Studie hat aus 1059 Kugeln 76 Rote, 167 Blaue und 816 Grüne. Meine Studie aus 150 Kugeln hat 10 Rote, 24 Blaue und 116 Grüne. Ich will die andere Studie mit meinen Daten validieren.
Vielen lieben Dank für Tipps und Antworten.
Wie beweise ich, dass die Häufigkeiten gleich sind?
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
- Lacrima013
- Grünschnabel

- Beiträge: 3
- Registriert: Di 9. Feb 2021, 12:16
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Wie beweise ich, dass die Häufigkeiten gleich sind?
Hallo Lacrima013,
ich glaube Dir nicht, dass in Deiner Studie bunte Kugeln aus Urnen gezogen wurden und möchte daher ganz generell auf meinen Punkt 8 aus diesem Thread verweisen: nutzung-des-forums-f44/das-musste-mal-gepostet-werden-t6682.html#p31013
Dort finden sich auch Quellen zu Primärliteratur.
Die Teststatisik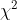 misst die Abweichung von der Zufallsverteilung -- sie wäre anwendbar, aber sie ist für sich genommen schwer interpretierbar.
misst die Abweichung von der Zufallsverteilung -- sie wäre anwendbar, aber sie ist für sich genommen schwer interpretierbar.
Der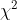 -Unabhängigkeitstest versucht immer nur, die Nullhypothese (kein Zusammenhang) zu wiederlegen. Wenn das nicht gelingt, kann es daran liegen, dass sie angenommen werden muss oder daran, dass Du noch nicht genügend gesampled hast. Der p-Wert unterscheidet nicht zwischen diesen beiden Optionen sondern fasst diese beiden zusammen. Eine posthoc-Fallzahlanalyse könnte ggf. helfen.
-Unabhängigkeitstest versucht immer nur, die Nullhypothese (kein Zusammenhang) zu wiederlegen. Wenn das nicht gelingt, kann es daran liegen, dass sie angenommen werden muss oder daran, dass Du noch nicht genügend gesampled hast. Der p-Wert unterscheidet nicht zwischen diesen beiden Optionen sondern fasst diese beiden zusammen. Eine posthoc-Fallzahlanalyse könnte ggf. helfen.
Ein anderer Ansatz ist der sogenannte BayesFactor. Man versucht zu modellieren, wie sehr man den beiden Thesen glauben sollte und erreichnet eine Statistik, die das Verhältnis der Glaubhaftikeit beider Hypothesen darstellt. Klingt ungewohnt, muss man sich erst einfinden, aber im Gegensatz zum p-Wert im klassischen Test kann man halt nicht nur die eine von beiden Hypothesen ablehnen, sondern Argumente für beide sammeln. Schön zusammengefasst in einer leicht interpretierbaren Zahl.
Einen guten Leseeinstieg findest Du im Kapitel "17.6 Bayesian statistics of contingency tables" in diesem online-Buch: https://learningstatisticswithr.com/boo ... ontingency
Wenn man das dort gewählte Vorgehen auf Deine Daten anwendet kann das so aussehen:
Du musst halt den Text lesen und schauen, ob in Deinem Fall "poisson" als sampleType wirklich passt.
Das Verhältnis der Glaubhaftigkeit der Zusammenhangshypothese zur Kein-Zusammenhangshypothese ist 1:0.006 bzw. 175:1 gegen die Kein-Zusammenhangshypothese. Dem Vorschlag des Buches folgend könnte man schreiben:
All analyses were conducted using the BayesFactor package in R , and unless otherwise stated default parameter values were used
A test of association produced a Bayes factor of 175:1 in favour of a relationship between the two studies.
Damit wäre die Zusammenhangshypothese mit "very strong evidence" untermauert.
Du musst Dir überlegen, ob dieser Ansatz für Dich taugt, oder ob eine posthoc-Poweranalyse vielleicht passender wäre.
LG,
Bernhard
ich glaube Dir nicht, dass in Deiner Studie bunte Kugeln aus Urnen gezogen wurden und möchte daher ganz generell auf meinen Punkt 8 aus diesem Thread verweisen: nutzung-des-forums-f44/das-musste-mal-gepostet-werden-t6682.html#p31013
Dort finden sich auch Quellen zu Primärliteratur.
Die Teststatisik
Der
Ein anderer Ansatz ist der sogenannte BayesFactor. Man versucht zu modellieren, wie sehr man den beiden Thesen glauben sollte und erreichnet eine Statistik, die das Verhältnis der Glaubhaftikeit beider Hypothesen darstellt. Klingt ungewohnt, muss man sich erst einfinden, aber im Gegensatz zum p-Wert im klassischen Test kann man halt nicht nur die eine von beiden Hypothesen ablehnen, sondern Argumente für beide sammeln. Schön zusammengefasst in einer leicht interpretierbaren Zahl.
Einen guten Leseeinstieg findest Du im Kapitel "17.6 Bayesian statistics of contingency tables" in diesem online-Buch: https://learningstatisticswithr.com/boo ... ontingency
Wenn man das dort gewählte Vorgehen auf Deine Daten anwendet kann das so aussehen:
- Code: Alles auswählen
m <- matrix(c(76, 167,816, 10, 24, 116), nrow = 2, byrow = TRUE)
print(m)
library(BayesFactor)
contingencyTableBF(m, sampleType = "poisson")[/quote]
mit dem Ergebnis
[code]> contingencyTableBF(m, sampleType = "poisson")
Bayes factor analysis
--------------
[1] Non-indep. (a=1) : 0.005715724 ±0%
Against denominator:
Null, independence, a = 1
---
Bayes factor type: BFcontingencyTable, poisson
Du musst halt den Text lesen und schauen, ob in Deinem Fall "poisson" als sampleType wirklich passt.
Das Verhältnis der Glaubhaftigkeit der Zusammenhangshypothese zur Kein-Zusammenhangshypothese ist 1:0.006 bzw. 175:1 gegen die Kein-Zusammenhangshypothese. Dem Vorschlag des Buches folgend könnte man schreiben:
All analyses were conducted using the BayesFactor package in R , and unless otherwise stated default parameter values were used
A test of association produced a Bayes factor of 175:1 in favour of a relationship between the two studies.
Damit wäre die Zusammenhangshypothese mit "very strong evidence" untermauert.
Du musst Dir überlegen, ob dieser Ansatz für Dich taugt, oder ob eine posthoc-Poweranalyse vielleicht passender wäre.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5947
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Wie beweise ich, dass die Häufigkeiten gleich sind?
Hallo Bernhard,
vielen lieben Dank für Deine schnelle und ausführliche Antwort. Ich bin hier ein Neuling und hätte mir vor meinem Post Deinen Thread und die Netiquette durchlesen sollen, danke für die Verlinkung.
Kurzgefasst geht es in meiner Studie (Diplomarbeit) um das Staging von Krebserkrankungen mittels zweier unterschiedlicher PET-CT-Methoden. Ich will prüfen, ob die Ergebnisse der anderen Studie auch auf mein Patientenkollektiv zutreffen. Angenommen die andere Studie hat mittels Methode1 von 1059 PET-CT Bildern in 76 (7.2%) Hirnmetastasen beschrieben, und meine Studie von 150 Bildern in 10 (6.9%): wie teste ich am Besten, ob mein Ergebnis mit dem Ergebnis der Studie übereinstimmt? Mein Ziel ist es, diese andere Studie zu verifizieren.
Wenn es mir also Mit dem Chi-Quadrat-Test nicht gelingt, die Nullhypothese (Kein Unterschied) zu verwerfen, dann darf ich nicht annehmen, dass die Null-Hypothese zutrifft, da eventuell nicht genügend gesampled wurde. Habe ich das richtig verstanden?
Mit der Bayesianischen Statistik bin ich leider noch nicht sehr vertraut, aber ich nehme Deinen Literaturvorschlag dankend an.
Falls die genauere Beschreibung meines Problems mehr Klarheit geschaffen hat, wäre ich über weitere Tipps sehr froh, ansonsten bedanke ich mich herzlich!
Liebe Grüße
vielen lieben Dank für Deine schnelle und ausführliche Antwort. Ich bin hier ein Neuling und hätte mir vor meinem Post Deinen Thread und die Netiquette durchlesen sollen, danke für die Verlinkung.
Kurzgefasst geht es in meiner Studie (Diplomarbeit) um das Staging von Krebserkrankungen mittels zweier unterschiedlicher PET-CT-Methoden. Ich will prüfen, ob die Ergebnisse der anderen Studie auch auf mein Patientenkollektiv zutreffen. Angenommen die andere Studie hat mittels Methode1 von 1059 PET-CT Bildern in 76 (7.2%) Hirnmetastasen beschrieben, und meine Studie von 150 Bildern in 10 (6.9%): wie teste ich am Besten, ob mein Ergebnis mit dem Ergebnis der Studie übereinstimmt? Mein Ziel ist es, diese andere Studie zu verifizieren.
Wenn es mir also Mit dem Chi-Quadrat-Test nicht gelingt, die Nullhypothese (Kein Unterschied) zu verwerfen, dann darf ich nicht annehmen, dass die Null-Hypothese zutrifft, da eventuell nicht genügend gesampled wurde. Habe ich das richtig verstanden?
Mit der Bayesianischen Statistik bin ich leider noch nicht sehr vertraut, aber ich nehme Deinen Literaturvorschlag dankend an.
Falls die genauere Beschreibung meines Problems mehr Klarheit geschaffen hat, wäre ich über weitere Tipps sehr froh, ansonsten bedanke ich mich herzlich!
Liebe Grüße
- Lacrima013
- Grünschnabel

- Beiträge: 3
- Registriert: Di 9. Feb 2021, 12:16
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Wie beweise ich, dass die Häufigkeiten gleich sind?
Hi,
- hast du Angaben zur Sensitivität und Spezifität der Messverfahren?
- wie sind die zwei Stichproben zustande gekommen?
- warum angenommen? Warum nicht: Das sind meine kreuztabellarischen Anzahlen?
Gruß
S.
- hast du Angaben zur Sensitivität und Spezifität der Messverfahren?
- wie sind die zwei Stichproben zustande gekommen?
- warum angenommen? Warum nicht: Das sind meine kreuztabellarischen Anzahlen?
Gruß
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4364
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Wie beweise ich, dass die Häufigkeiten gleich sind?
Lacrima013 hat geschrieben:Wenn es mir also Mit dem Chi-Quadrat-Test nicht gelingt, die Nullhypothese (Kein Unterschied) zu verwerfen, dann darf ich nicht annehmen, dass die Null-Hypothese zutrifft, da eventuell nicht genügend gesampled wurde. Habe ich das richtig verstanden?
Das gilt für den p-Wert als Ergebnis des Tests für sich allein genommen. Wenn Du anderweitig begründen kannst, dass Du ausreichend Daten gesammelt hast um eine ausreichende Genauigkeit zu erreichen, dann ist das etwas anderes. Dein Test steht einer Gleichheit/Unabhängigkeit nicht im Wege -- das ist schon mal gut. Ob n = 150 längst eine ausreichende Samplingmenge ist kann je nach Anspruch entweder bei Augenscheinbeweis erbracht werden, wenn Deine Betreuer finden, dass 150 "schon sehr viel" ist oder Du musst was rechnen -- das hängt vom Anspruch der Arbeit ab.
Mit der Bayesianischen Statistik bin ich leider noch nicht sehr vertraut, aber ich nehme Deinen Literaturvorschlag dankend an.
Ich habe nicht gesagt, dass das der einzig richtige Weg sei, aber es ist einer, über den Du auch nachdenken solltest.
Falls die genauere Beschreibung meines Problems mehr Klarheit geschaffen hat, wäre ich über weitere Tipps sehr froh, ansonsten bedanke ich mich herzlich!
Mir bleibt das unklar. Wenn Du in einer anderen Studie an einem anderen Ort andere Populationen untersuchst ist mir überhaupt nicht klar, warum da der Anteil an Hirnmetastasen der gleiche sein sollte. Wenn Du die gleiche Population untersuchst, vielleicht sogar gleiche Individuen, dann müsste man sich Gedanken machen, ob das wirklich unabhängige Samples sind, die Voraussetzung für Chi-Quadrat und Fisher sind, aber ich unterstelle jetzt einfach mal, dass Du Dir das schon überlegt haben wirst.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5947
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Wie beweise ich, dass die Häufigkeiten gleich sind?
Hi,
schon mal danke für Deine Hilfe!
Sensitivität und Spezifität sind je nach dem was getestet wird (Primär Tumor, Lymphknotenmetastasen, sekundär Tumor) unterschiedlich. Sollte ich hier meinen Ansatz suchen?
Die Stichproben bestehen aus PatientInnen, welche von verschiedenen Institutionen aufgrund einer suspekten Raumforderung ein PET-CT erhalten haben, oder bei denen rezent ein Tumor diagnostiziert wurde. Gleiches gilt für meine Stichprobe. Ist dadurch die Unabhängigkeit noch gegeben? Ich dachte schon.
"Angenommen", weil ich noch keine eigenen Daten erhoben habe. Ich erstelle momentan den Projektplan, und möchte die statistischen Methoden so genau wie möglich angeben. Meine angenommen Daten habe ich mir ausgedacht, um Teststatistiken durchzurechnen.
Bezüglich unabhängige Stichproben habe ich meine Zweifel bereits in der Antwort an strukturmarionette beschrieben.
Vielleicht schafft es mehr Klarheit die 2 Methoden zu beschreiben. Die erste Methode ist das Standardverfahren für das Tumorstaging. Es wird der ganze Körper gescannt (Wie groß ist der primär Tumor, gibt es Lymphknotenmetastasen, gibt es sekundär Tumore?). Die zweite Methode scannt nur einen gewissen Teil des Körpers. Die zu validierende Studie behauptet, dass es nur in 1,2% der 1059 PatientInnen aufgrund eines anderen Staging mittels Methode 2, welche billiger und schneller ist, zu einer anderen Therapie geführt hat (bsp. palliativ -> kurativ).
Mein Ziel ist es zu beweisen, dass die zweite Methode auch bei meinem Patientenkollektiv nur in wenigen Fällen in diesem Prozentbereich zu einem "change in therapy" geführt hat, und diese Methode in Zukunft angewendet werden kann.
Viel Dank für Eure Mühe und viele Grüße!
schon mal danke für Deine Hilfe!
strukturmarionette hat geschrieben:Hi,
- hast du Angaben zur Sensitivität und Spezifität der Messverfahren?
- wie sind die zwei Stichproben zustande gekommen?
- warum angenommen? Warum nicht: Das sind meine kreuztabellarischen Anzahlen?
Gruß
S.
Sensitivität und Spezifität sind je nach dem was getestet wird (Primär Tumor, Lymphknotenmetastasen, sekundär Tumor) unterschiedlich. Sollte ich hier meinen Ansatz suchen?
Die Stichproben bestehen aus PatientInnen, welche von verschiedenen Institutionen aufgrund einer suspekten Raumforderung ein PET-CT erhalten haben, oder bei denen rezent ein Tumor diagnostiziert wurde. Gleiches gilt für meine Stichprobe. Ist dadurch die Unabhängigkeit noch gegeben? Ich dachte schon.
"Angenommen", weil ich noch keine eigenen Daten erhoben habe. Ich erstelle momentan den Projektplan, und möchte die statistischen Methoden so genau wie möglich angeben. Meine angenommen Daten habe ich mir ausgedacht, um Teststatistiken durchzurechnen.
bele hat geschrieben:
Mir bleibt das unklar. Wenn Du in einer anderen Studie an einem anderen Ort andere Populationen untersuchst ist mir überhaupt nicht klar, warum da der Anteil an Hirnmetastasen der gleiche sein sollte. Wenn Du die gleiche Population untersuchst, vielleicht sogar gleiche Individuen, dann müsste man sich Gedanken machen, ob das wirklich unabhängige Samples sind, die Voraussetzung für Chi-Quadrat und Fisher sind, aber ich unterstelle jetzt einfach mal, dass Du Dir das schon überlegt haben wirst.
Bezüglich unabhängige Stichproben habe ich meine Zweifel bereits in der Antwort an strukturmarionette beschrieben.
Vielleicht schafft es mehr Klarheit die 2 Methoden zu beschreiben. Die erste Methode ist das Standardverfahren für das Tumorstaging. Es wird der ganze Körper gescannt (Wie groß ist der primär Tumor, gibt es Lymphknotenmetastasen, gibt es sekundär Tumore?). Die zweite Methode scannt nur einen gewissen Teil des Körpers. Die zu validierende Studie behauptet, dass es nur in 1,2% der 1059 PatientInnen aufgrund eines anderen Staging mittels Methode 2, welche billiger und schneller ist, zu einer anderen Therapie geführt hat (bsp. palliativ -> kurativ).
Mein Ziel ist es zu beweisen, dass die zweite Methode auch bei meinem Patientenkollektiv nur in wenigen Fällen in diesem Prozentbereich zu einem "change in therapy" geführt hat, und diese Methode in Zukunft angewendet werden kann.
Viel Dank für Eure Mühe und viele Grüße!
- Lacrima013
- Grünschnabel

- Beiträge: 3
- Registriert: Di 9. Feb 2021, 12:16
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: Wie beweise ich, dass die Häufigkeiten gleich sind?
Hallo Lacrima,
Das ist im Prinzip eine sehr gute Idee und ich kann Dir dazu nur gratulieren.
Das verstehe ich nur bedingt. Wenn die Studie validierungsbedürftig ist, dann sollte man vorübergehend Standardverfahren/Goldstandard und Alternativverfahren gleichzeitig durchführen und kann dann mit verbundenen Stichproben Testgütekriterien bestimmen. Ansonsten finde ich aus medizinischer Sicht, die Frage nach identischer Verteilung zu anspruchsvoll. Nochmal: Niemand kann bei unterschiedlichen Populationen erwarten, dass die Krankheitsausprägungen so ähnlich sind, dass ein Verfahren zu gleichen Teilen einen "Change in Therapy" bewirken. Ich finde diese Fragestellung schlicht nicht testenswert.
Dann bestimme ein 95%-Konfidenzintervall für den Anteil der Patienten, bei denen das neue Verfahren einen Einfluss auf die Therapie hatte, berichte dieses und diskutiere, ob man das mit "nur wenige Fälle" angemessen beschreiben kann.
LG,
Bernhard
Lacrima013 hat geschrieben:"Angenommen", weil ich noch keine eigenen Daten erhoben habe. Ich erstelle momentan den Projektplan, und möchte die statistischen Methoden so genau wie möglich angeben. Meine angenommen Daten habe ich mir ausgedacht, um Teststatistiken durchzurechnen.
Das ist im Prinzip eine sehr gute Idee und ich kann Dir dazu nur gratulieren.
.Vielleicht schafft es mehr Klarheit die 2 Methoden zu beschreiben. Die erste Methode ist das Standardverfahren für das Tumorstaging. Es wird der ganze Körper gescannt (Wie groß ist der primär Tumor, gibt es Lymphknotenmetastasen, gibt es sekundär Tumore?). Die zweite Methode scannt nur einen gewissen Teil des Körpers. Die zu validierende Studie behauptet, dass es nur in 1,2% der 1059 PatientInnen aufgrund eines anderen Staging mittels Methode 2, welche billiger und schneller ist, zu einer anderen Therapie geführt hat (bsp. palliativ -> kurativ)
Das verstehe ich nur bedingt. Wenn die Studie validierungsbedürftig ist, dann sollte man vorübergehend Standardverfahren/Goldstandard und Alternativverfahren gleichzeitig durchführen und kann dann mit verbundenen Stichproben Testgütekriterien bestimmen. Ansonsten finde ich aus medizinischer Sicht, die Frage nach identischer Verteilung zu anspruchsvoll. Nochmal: Niemand kann bei unterschiedlichen Populationen erwarten, dass die Krankheitsausprägungen so ähnlich sind, dass ein Verfahren zu gleichen Teilen einen "Change in Therapy" bewirken. Ich finde diese Fragestellung schlicht nicht testenswert.
Mein Ziel ist es zu beweisen, dass die zweite Methode auch bei meinem Patientenkollektiv nur in wenigen Fällen in diesem Prozentbereich zu einem "change in therapy" geführt hat, und diese Methode in Zukunft angewendet werden kann.
Dann bestimme ein 95%-Konfidenzintervall für den Anteil der Patienten, bei denen das neue Verfahren einen Einfluss auf die Therapie hatte, berichte dieses und diskutiere, ob man das mit "nur wenige Fälle" angemessen beschreiben kann.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5947
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
Zurück zu Kreuztabellen & Chi²
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 2 Gäste


