Liebe Forengemeinschaft,
ich möchte mir euren Ratschlag zu folgendem Fall einholen:
Ich möchte die m²-Preise für Bauland für die kommenden Jahren prognostizieren bzw. schätzen.
Es liegen 100 Fälle von verkauften Baugrundstücken aus den letzten 4 Jahren vor, welche über diese zufällig verteilt sind (mit manchmal größeren Lücken, also Monaten, wo kein Grundstück verkauft wurde).
Ich habe also die Variablen m²-Preis in € sowie Kaufdatum.
Welche Verfahren würden sich eurer Meinung nach am Besten eignen, wenn ich die Preise der kommenden Jahre richtig schätzen bzw. prognostizieren möchte?
Vielen Dank für eure Aufmerksamkeit!
Welches Verfahren für Prognosen oder Schätzungen?
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
- Lupo123
- Beobachter

- Beiträge: 11
- Registriert: Di 20. Feb 2018, 12:45
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren für Prognosen oder Schätzungen?
Hi,
- sich über sinnvolle Prädiktorvariablen Gedanken zu machen
Gruß
S.
- sich über sinnvolle Prädiktorvariablen Gedanken zu machen
Gruß
S.
- strukturmarionette
- Schlaflos in Seattle

- Beiträge: 4369
- Registriert: Fr 17. Jun 2011, 22:15
- Danke gegeben: 32
- Danke bekommen: 587 mal in 584 Posts
Re: Welches Verfahren für Prognosen oder Schätzungen?
strukturmarionette hat geschrieben:Hi,
- sich über sinnvolle Prädiktorvariablen Gedanken zu machen
Gruß
S.
Was, wenn ich nur diese Daten habe?
An dieses Problem habe ich schon gedacht, bei der Idee, die Zeitreihenanalyse anzuwenden. Die ist, wie viel ich verstanden habe, eine Form der Regression, und da braucht es eine unabhängige Variable.
Ich habe eine Regression bereits mit den zwei vorhandenen Variablen (Kaufpreis und Datum) vollzogen, bekam aber ein R von 0,2 - was ja eindeutig zu wenig ist. Ich fürchte, dass das Resultat daher nicht aussagekräftig ist.
- Lupo123
- Beobachter

- Beiträge: 11
- Registriert: Di 20. Feb 2018, 12:45
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren für Prognosen oder Schätzungen?
Hi!
Ich kenne mich da nicht aus, aber mir hat mal wer gesagt, dass der Grundstückspreis hauptsächlich von den drei großen "L" abhängt: "Lage", "Lage" und "Lage". Wenn Du jetzt zeigen kannst, dass 20% der Preisunterschiede gar nicht durch die Lage, sondern durch einen Trend über die Zeit zu erklären sind, warum ist das dann nicht aussagekräftig?
Ich würde jetzt erstmal eine Punktwolke plotten (Streudiagramm) und schauen, ob die Punkte auf einer Linie liegen, durch die mal plausibel eine Funktion legen kann oder ob das wirklich eine "Wolke" ist, die durch eine Linie nur schlecht zu beschreiben ist.
Wenn Du Durch Deine 100 Punkte jetzt ein Polinom 50. Grades legst, dann bekommst Du ein traumhaftes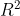 und kannst Dich darauf Verlassen, dass Prognosen aus diesem Polinom ganz, ganz extrem weit weg von der Wahrheit liegen werden. Beiß Dich also nicht zu sehr am
und kannst Dich darauf Verlassen, dass Prognosen aus diesem Polinom ganz, ganz extrem weit weg von der Wahrheit liegen werden. Beiß Dich also nicht zu sehr am 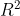 fest, versuche vor allem Wissen über das Verhalten von Baulandpreisen in die Modellbildung einfließen zu lassen.
fest, versuche vor allem Wissen über das Verhalten von Baulandpreisen in die Modellbildung einfließen zu lassen.
Und wie gesagt: Schau Dir unbedingt die Daten als Grafik an, dann kannst Du Deine Erwartungshaltung mit der Realität abgleichen.
LG,
Bernhard
Lupo123 hat geschrieben:Ich habe eine Regression bereits mit den zwei vorhandenen Variablen (Kaufpreis und Datum) vollzogen, bekam aber ein R von 0,2 - was ja eindeutig zu wenig ist. Ich fürchte, dass das Resultat daher nicht aussagekräftig ist.
Ich kenne mich da nicht aus, aber mir hat mal wer gesagt, dass der Grundstückspreis hauptsächlich von den drei großen "L" abhängt: "Lage", "Lage" und "Lage". Wenn Du jetzt zeigen kannst, dass 20% der Preisunterschiede gar nicht durch die Lage, sondern durch einen Trend über die Zeit zu erklären sind, warum ist das dann nicht aussagekräftig?
Ich würde jetzt erstmal eine Punktwolke plotten (Streudiagramm) und schauen, ob die Punkte auf einer Linie liegen, durch die mal plausibel eine Funktion legen kann oder ob das wirklich eine "Wolke" ist, die durch eine Linie nur schlecht zu beschreiben ist.
Wenn Du Durch Deine 100 Punkte jetzt ein Polinom 50. Grades legst, dann bekommst Du ein traumhaftes
Und wie gesagt: Schau Dir unbedingt die Daten als Grafik an, dann kannst Du Deine Erwartungshaltung mit der Realität abgleichen.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Welches Verfahren für Prognosen oder Schätzungen?
bele hat geschrieben:Hi!Lupo123 hat geschrieben:Ich habe eine Regression bereits mit den zwei vorhandenen Variablen (Kaufpreis und Datum) vollzogen, bekam aber ein R von 0,2 - was ja eindeutig zu wenig ist. Ich fürchte, dass das Resultat daher nicht aussagekräftig ist.
Ich kenne mich da nicht aus, aber mir hat mal wer gesagt, dass der Grundstückspreis hauptsächlich von den drei großen "L" abhängt: "Lage", "Lage" und "Lage". Wenn Du jetzt zeigen kannst, dass 20% der Preisunterschiede gar nicht durch die Lage, sondern durch einen Trend über die Zeit zu erklären sind, warum ist das dann nicht aussagekräftig?
Hi! Hmmm ja, ich kenne mich da selber nicht aus, deshalb dachte ich, das wäre nicht aussagekräftig. Das heißt, Prognosen mit einer Regression sind auch mit einer Variable, die nur einen geringen Anteil der abhängigen Variable erklärt, zulässig?
bele hat geschrieben:Ich würde jetzt erstmal eine Punktwolke plotten (Streudiagramm) und schauen, ob die Punkte auf einer Linie liegen, durch die mal plausibel eine Funktion legen kann oder ob das wirklich eine "Wolke" ist, die durch eine Linie nur schlecht zu beschreiben ist.
Wenn Du Durch Deine 100 Punkte jetzt ein Polinom 50. Grades legst, dann bekommst Du ein traumhaftesund kannst Dich darauf Verlassen, dass Prognosen aus diesem Polinom ganz, ganz extrem weit weg von der Wahrheit liegen werden. Beiß Dich also nicht zu sehr am
fest, versuche vor allem Wissen über das Verhalten von Baulandpreisen in die Modellbildung einfließen zu lassen.
Und wie gesagt: Schau Dir unbedingt die Daten als Grafik an, dann kannst Du Deine Erwartungshaltung mit der Realität abgleichen.
LG,
Bernhard
Das habe ich in der Tat schon letzte Woche gemacht, wobei das hier rausgekommen war:

Ich habe mich übrigens geirrt, es sind 19 Fälle, nicht 100. Die anderen Fälle sind Grundstücke, auf denen Gebäude stehen. Ich berechne hier aber nur die Preise für leere Baugrundstücke. Da stelle ich mir natürlich auch die Frage, ob das überhaupt genug Fälle sind, um damit sinnvolle statistische Rechnungen anstellen zu können.
Ich möchte das aber für meine Gemeinde berechnen, und da sind in diesen letzten Jahren nunmal nur diese 19 Baugrundstücke verkauft worden.
Denkt ihr also, ich kann ohne Zweifel die Regression zur Prognose heranziehen?
- Lupo123
- Beobachter

- Beiträge: 11
- Registriert: Di 20. Feb 2018, 12:45
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren für Prognosen oder Schätzungen?
Hallo Lupo,
Was ein geringer und was ein großer Anteil der erklärten Varianz ist hängt immer von Thema, Fragestellung, Messmethoden etc. ab. Ein Prozent Varianzaufklärung kann nobelpreisverdächtig sein, 99% Varianzaufklärung können zum Gähnen sein.
Stell Dir vor, Du hättest 1915 , dem Jahr nachdem die Spezielle Relativitätstheorie publiziert wurde, mit "nur" 1% Varianzaufklärung aber hoher Sicherheit zeigen können, dass eine Uhr in der nähe einer großen Masse langsamer läuft als entfernt von allen Massen. Die Einstein-Lupo-Theorie wäre mindestens dem Namen nach jedem bekannt. Wenn Du nun aber aus dem Datum die Jahreszeit vorhersagen könntest, würde das mutmaßlich keinen interessieren. Schon gar nicht bei "nur" 93% Varianzaufklärung.
Statistik ist dazu da, mit natürlich verbleibenden Zweifeln rational umzugehen. Wenn man etwas "ohne Zweifel" annehmen kann, braucht man keine Statistik. Es sind aber nicht die 24% Varianzaufklärung an denen ich zweifeln würde. Da hat jemand 2017 fast 600€/qm bekommen, alle anderen aber nur maximal 400€/qm. Dieser eine Fall hat mutmaßlich erheblichen Einfluss auf die Steigung Deiner Geraden. Versuch herauszufinden, wer das war und was das für ein Grundstück war. War es ein Grundstück mit Seeblick? Oder hat das der Sohn des Bürgermeisters an die Gemeinde verkauft? Wenn ja, gibt es nur das eine Grundstück mit Seeblick oder werden in der Zukunft noch weitere Grundstücke mit Seeblick verkauft werden? Warum hat im Juli 2018 ein Grundstück für nur 200€/qm den Besitzer gewechselt? Hat das die Gemeinde an den Sohn des Bürgermeisters verkauft oder hat sich da eine riesige landwirtschaftliche Nutzfläche in die Baugrundstücksliste eingeschlichen, weil man auf den Acker einen Schuppen ohne Anschluss an die Wasserversorgung stellen darf?
Mindestens für diese beiden Extremfälle, vielleicht auch noch für den im März 2017 und den im Februar 2020 solltest Du erstens Recherchen anstellen, ob das begründete Einzelfälle waren, die in die Prognose nicht hinein gehören und zweitens die Regression nochmal ohne sie rechnen und schauen, ob die Regressionsgerade erheblich abweicht.
Wenn man nur 19 Beobachtungen hat und die Punkte, so wie bei Dir, leidlich auf einer Geraden liegen, ist lineare Regression eine insgesamt vernünftige Entscheidung. Es muss Dir nur klar sein, dass die Wahrheit nicht linear ist und dass Du nicht von den Jahren 2017 bis 2020 Vorhersagen machen kannst, was Dein Grundstück in 20 Jahren Wert sein wird.
LG,
Bernhard
Lupo123 hat geschrieben:Das heißt, Prognosen mit einer Regression sind auch mit einer Variable, die nur einen geringen Anteil der abhängigen Variable erklärt, zulässig?
Was ein geringer und was ein großer Anteil der erklärten Varianz ist hängt immer von Thema, Fragestellung, Messmethoden etc. ab. Ein Prozent Varianzaufklärung kann nobelpreisverdächtig sein, 99% Varianzaufklärung können zum Gähnen sein.
Stell Dir vor, Du hättest 1915 , dem Jahr nachdem die Spezielle Relativitätstheorie publiziert wurde, mit "nur" 1% Varianzaufklärung aber hoher Sicherheit zeigen können, dass eine Uhr in der nähe einer großen Masse langsamer läuft als entfernt von allen Massen. Die Einstein-Lupo-Theorie wäre mindestens dem Namen nach jedem bekannt. Wenn Du nun aber aus dem Datum die Jahreszeit vorhersagen könntest, würde das mutmaßlich keinen interessieren. Schon gar nicht bei "nur" 93% Varianzaufklärung.
Das habe ich in der Tat schon letzte Woche gemacht, wobei das hier rausgekommen war:bele hat geschrieben:Ich würde jetzt erstmal eine Punktwolke plotten (Streudiagramm) und schauen, ob die Punkte auf einer Linie liegen, durch die mal plausibel eine Funktion legen kann oder ob das wirklich eine "Wolke" ist, die durch eine Linie nur schlecht zu beschreiben ist.
[...]
Ich möchte das aber für meine Gemeinde berechnen, und da sind in diesen letzten Jahren nunmal nur diese 19 Baugrundstücke verkauft worden.
Denkt ihr also, ich kann ohne Zweifel die Regression zur Prognose heranziehen?
Statistik ist dazu da, mit natürlich verbleibenden Zweifeln rational umzugehen. Wenn man etwas "ohne Zweifel" annehmen kann, braucht man keine Statistik. Es sind aber nicht die 24% Varianzaufklärung an denen ich zweifeln würde. Da hat jemand 2017 fast 600€/qm bekommen, alle anderen aber nur maximal 400€/qm. Dieser eine Fall hat mutmaßlich erheblichen Einfluss auf die Steigung Deiner Geraden. Versuch herauszufinden, wer das war und was das für ein Grundstück war. War es ein Grundstück mit Seeblick? Oder hat das der Sohn des Bürgermeisters an die Gemeinde verkauft? Wenn ja, gibt es nur das eine Grundstück mit Seeblick oder werden in der Zukunft noch weitere Grundstücke mit Seeblick verkauft werden? Warum hat im Juli 2018 ein Grundstück für nur 200€/qm den Besitzer gewechselt? Hat das die Gemeinde an den Sohn des Bürgermeisters verkauft oder hat sich da eine riesige landwirtschaftliche Nutzfläche in die Baugrundstücksliste eingeschlichen, weil man auf den Acker einen Schuppen ohne Anschluss an die Wasserversorgung stellen darf?
Mindestens für diese beiden Extremfälle, vielleicht auch noch für den im März 2017 und den im Februar 2020 solltest Du erstens Recherchen anstellen, ob das begründete Einzelfälle waren, die in die Prognose nicht hinein gehören und zweitens die Regression nochmal ohne sie rechnen und schauen, ob die Regressionsgerade erheblich abweicht.
Wenn man nur 19 Beobachtungen hat und die Punkte, so wie bei Dir, leidlich auf einer Geraden liegen, ist lineare Regression eine insgesamt vernünftige Entscheidung. Es muss Dir nur klar sein, dass die Wahrheit nicht linear ist und dass Du nicht von den Jahren 2017 bis 2020 Vorhersagen machen kannst, was Dein Grundstück in 20 Jahren Wert sein wird.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Welches Verfahren für Prognosen oder Schätzungen?
bele hat geschrieben:Hallo Lupo,Lupo123 hat geschrieben:Das heißt, Prognosen mit einer Regression sind auch mit einer Variable, die nur einen geringen Anteil der abhängigen Variable erklärt, zulässig?
Was ein geringer und was ein großer Anteil der erklärten Varianz ist hängt immer von Thema, Fragestellung, Messmethoden etc. ab. Ein Prozent Varianzaufklärung kann nobelpreisverdächtig sein, 99% Varianzaufklärung können zum Gähnen sein.
Stell Dir vor, Du hättest 1915 , dem Jahr nachdem die Spezielle Relativitätstheorie publiziert wurde, mit "nur" 1% Varianzaufklärung aber hoher Sicherheit zeigen können, dass eine Uhr in der nähe einer großen Masse langsamer läuft als entfernt von allen Massen. Die Einstein-Lupo-Theorie wäre mindestens dem Namen nach jedem bekannt. Wenn Du nun aber aus dem Datum die Jahreszeit vorhersagen könntest, würde das mutmaßlich keinen interessieren. Schon gar nicht bei "nur" 93% Varianzaufklärung.
Verstehe ich das richtig, dass diese Varianzaufklärung die Abweichung der einzelnen Messungen von der theoretischen Linie ist? Ich habe das irgendwie so in Erinnerung. In meinem Fall wäre das also ein sehr schwaches R, da mein Ziel es ja ist, die m²-Preise in den kommenden Jahre möglichst richtig zu schätzen, und dieses R dafür nunmal zu schwach ist (für die kommenden zwanzig Jahre muss es nicht sein, ich möchte es erst einmal für die kommenden Jahre bestimmen können).
bele hat geschrieben:bele hat geschrieben:Das habe ich in der Tat schon letzte Woche gemacht, wobei das hier rausgekommen war:bele hat geschrieben:Ich würde jetzt erstmal eine Punktwolke plotten (Streudiagramm) und schauen, ob die Punkte auf einer Linie liegen, durch die mal plausibel eine Funktion legen kann oder ob das wirklich eine "Wolke" ist, die durch eine Linie nur schlecht zu beschreiben ist.
[...]
Ich möchte das aber für meine Gemeinde berechnen, und da sind in diesen letzten Jahren nunmal nur diese 19 Baugrundstücke verkauft worden.
Denkt ihr also, ich kann ohne Zweifel die Regression zur Prognose heranziehen?
Statistik ist dazu da, mit natürlich verbleibenden Zweifeln rational umzugehen. Wenn man etwas "ohne Zweifel" annehmen kann, braucht man keine Statistik. Es sind aber nicht die 24% Varianzaufklärung an denen ich zweifeln würde. Da hat jemand 2017 fast 600€/qm bekommen, alle anderen aber nur maximal 400€/qm. Dieser eine Fall hat mutmaßlich erheblichen Einfluss auf die Steigung Deiner Geraden. Versuch herauszufinden, wer das war und was das für ein Grundstück war. War es ein Grundstück mit Seeblick? Oder hat das der Sohn des Bürgermeisters an die Gemeinde verkauft? Wenn ja, gibt es nur das eine Grundstück mit Seeblick oder werden in der Zukunft noch weitere Grundstücke mit Seeblick verkauft werden? Warum hat im Juli 2018 ein Grundstück für nur 200€/qm den Besitzer gewechselt? Hat das die Gemeinde an den Sohn des Bürgermeisters verkauft oder hat sich da eine riesige landwirtschaftliche Nutzfläche in die Baugrundstücksliste eingeschlichen, weil man auf den Acker einen Schuppen ohne Anschluss an die Wasserversorgung stellen darf?
Mindestens für diese beiden Extremfälle, vielleicht auch noch für den im März 2017 und den im Februar 2020 solltest Du erstens Recherchen anstellen, ob das begründete Einzelfälle waren, die in die Prognose nicht hinein gehören und zweitens die Regression nochmal ohne sie rechnen und schauen, ob die Regressionsgerade erheblich abweicht.
Wenn man nur 19 Beobachtungen hat und die Punkte, so wie bei Dir, leidlich auf einer Geraden liegen, ist lineare Regression eine insgesamt vernünftige Entscheidung. Es muss Dir nur klar sein, dass die Wahrheit nicht linear ist und dass Du nicht von den Jahren 2017 bis 2020 Vorhersagen machen kannst, was Dein Grundstück in 20 Jahren Wert sein wird.
LG,
Bernhard
Verstehe, verstehe. Danke für die Ratschläge. Ich habe alle Ausreißer entfernt, und tatsächlich komme ich jetzt anscheinend auf ein R² von 0,548. Das ist schon deutlich besser.
Was genau bedeutet das nun aus mathematischer Sicht, wenn ich den Kaufpreis für die kommenden Jahre mithilfe der Regressionskoeffizienten schätze? Jetzt vor allem in Hinsicht auf die erklärte Varianz. Bedeutet das, dass die Werte noch zu (1 – 0,548)% variieren können, da hier weitere Merkmale für eine genauere Prognose fehlen? Also sozusagen, dass die Werte noch zu 50% von der theoretischen Regressionsgeraden abweichen könnten?
Habe übrigens noch eine andere Frage, weil ich mir gar nicht sicher bin, ob ich die Regression überhaupt richtig berechne (ich mache das alles in SPSS): Und zwar ob ich das Kaufdatum als Variable verwenden kann, oder ob ich das irgendwie umformen muss in einzelne Werte? Ich weiß nämlich nicht, wie SPSS damit umgeht. Als ich die Regression "händisch" gelernt habe, haben wir bei der Zeitreihenanalyse z.B. bei den Jahren Absolutwerte verwendet, also 1 für das erste Jahr, 2 für das zweite, etc.
In diesem Fall hier müsste ich das wohl für Tage machen, nur werden dann die meisten Tage keine Werte (keinen Kaufpreis, etc.) haben, da an den meisten Tagen ja kein Grundstück verkauft wurde.
- Lupo123
- Beobachter

- Beiträge: 11
- Registriert: Di 20. Feb 2018, 12:45
- Danke gegeben: 4
- Danke bekommen: 0 mal in 0 Post
Re: Welches Verfahren für Prognosen oder Schätzungen?
Hallo Lupo,
Nochmal, der Preis wird abhängen von der Lage, der Anbindung an die Straßen, ob man einen Vorgarten nach Süden haben muss oder den eigentlichen Garten nach Süden haben kann, von der Höhe des Gründstücks (läuft es bei Starkregen von meinem auf das Grundstück des Nachbarn oder von seinem auf mein Grundstück) und hundert weiteren Dingen. Was hast Du denn erwartet, wie genau Du mit einem Datum allein vorhersagen kannst, auf welchen Preis Verkäufer und Käufer sich einigen werden?
Ein besseres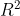 durch Weglassen von Ausreißern bedeutet nicht automatisch auch eine bessere Vorhersagekraft des Modells. Wenn Du alle bis auf zwei Punkte löschst, dann erreichst Du 100% Varianzaufklärung. Das bedeutet aber nicht, dass sich der Quadratmeterpreis in Deiner Gemeinde damit zu 100% aus dem Datum vorhersagen ließe.
durch Weglassen von Ausreißern bedeutet nicht automatisch auch eine bessere Vorhersagekraft des Modells. Wenn Du alle bis auf zwei Punkte löschst, dann erreichst Du 100% Varianzaufklärung. Das bedeutet aber nicht, dass sich der Quadratmeterpreis in Deiner Gemeinde damit zu 100% aus dem Datum vorhersagen ließe.
Ich habe auch nicht gesagt, dass Du Ausreißer mal weglassen sollst, um das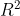 zu verbessern, sondern um zu schauen, wie das die Koeffizienten beeinflusst.
zu verbessern, sondern um zu schauen, wie das die Koeffizienten beeinflusst.
Nein.
Sorry, zu SPSS kann ich garnichts sagen. Vielleicht meldet sich jemand anderes dazu. Ich gehe aber davon aus, dass das von den Programmierern von SPSS schon vernünftig gelöst wurde und vermute daher, dass Du nichts weiter machen musst. Sollte sich hier keiner zu der Frage äußern, frag beispielsweise hier: http://www.spss-forum.de
LG,
Bernhard
Lupo123 hat geschrieben:Verstehe ich das richtig, dass diese Varianzaufklärung die Abweichung der einzelnen Messungen von der theoretischen Linie ist? Ich habe das irgendwie so in Erinnerung. In meinem Fall wäre das also ein sehr schwaches R, da mein Ziel es ja ist, die m²-Preise in den kommenden Jahre möglichst richtig zu schätzen, und dieses R dafür nunmal zu schwach ist (für die kommenden zwanzig Jahre muss es nicht sein, ich möchte es erst einmal für die kommenden Jahre bestimmen können).
Nochmal, der Preis wird abhängen von der Lage, der Anbindung an die Straßen, ob man einen Vorgarten nach Süden haben muss oder den eigentlichen Garten nach Süden haben kann, von der Höhe des Gründstücks (läuft es bei Starkregen von meinem auf das Grundstück des Nachbarn oder von seinem auf mein Grundstück) und hundert weiteren Dingen. Was hast Du denn erwartet, wie genau Du mit einem Datum allein vorhersagen kannst, auf welchen Preis Verkäufer und Käufer sich einigen werden?
Verstehe, verstehe. Danke für die Ratschläge. Ich habe alle Ausreißer entfernt, und tatsächlich komme ich jetzt anscheinend auf ein R² von 0,548. Das ist schon deutlich besser.
Ein besseres
Ich habe auch nicht gesagt, dass Du Ausreißer mal weglassen sollst, um das
Jetzt vor allem in Hinsicht auf die erklärte Varianz. Bedeutet das, dass die Werte noch zu (1 – 0,548)% variieren können, da hier weitere Merkmale für eine genauere Prognose fehlen? Also sozusagen, dass die Werte noch zu 50% von der theoretischen Regressionsgeraden abweichen könnten?
Nein.
(ich mache das alles in SPSS): Und zwar ob ich das Kaufdatum als Variable verwenden kann, oder ob ich das irgendwie umformen muss in einzelne Werte? Ich weiß nämlich nicht, wie SPSS damit umgeht.
Sorry, zu SPSS kann ich garnichts sagen. Vielleicht meldet sich jemand anderes dazu. Ich gehe aber davon aus, dass das von den Programmierern von SPSS schon vernünftig gelöst wurde und vermute daher, dass Du nichts weiter machen musst. Sollte sich hier keiner zu der Frage äußern, frag beispielsweise hier: http://www.spss-forum.de
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 5 Gäste


