Hallo zusammen.
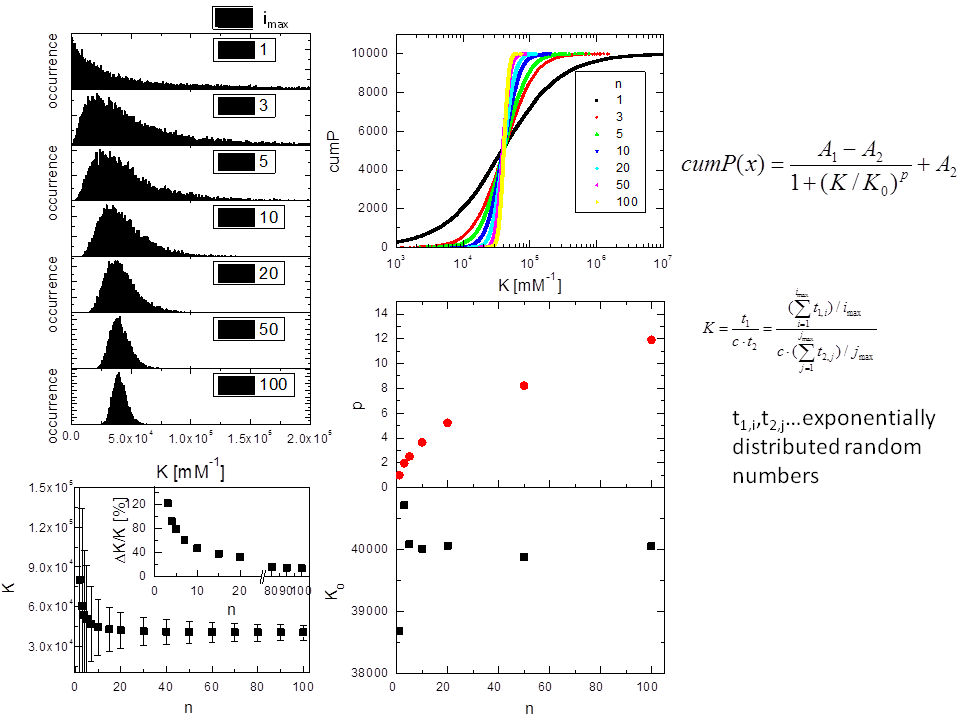
In der angehängten Datei habe ich das Problem grafisch zusammengefasst, welches mich interessiert. Ich möchte wissen mit welchen analytischen Funktionen ich die Verteilungen von K auf der linken Seite beschreiben kann.
K = t1/(c*t2) und t1 bzw. t2 sind Mittelwerte mono-exponential verteilter Zufallszahlen t1,i bzw. t1,j mit dem Erwartungswert t1 und t2 (Matlab: 'random('exp',10)',imax,2). In der Grafik ist sind die Erwartungswerte beide 10 und in der Berechnung für K gibt es noch eine Konstante c. Insgesamt wurden 10000 K Werte generiert und als Histogramm zusammengefasst. Die Konstante c hat mit dem Ursprung in der Chemie zu tun, welche hier zugrunde liegt. Das c ist aber konstant, sollte also nicht weiter stören.
Ich habe mir damit geholfen die K-Verteilungen kumulativ darzustellen und mit einer Logistikfunktion anzupassen, was recht gut funktioniert.
Im Grunde möchte ich aber am Ende bei bekanntem i_max wissen welche Funktion ich benutzen müsste um bspw. 2 oder 3 überlagerte K-Verteilungen voneinander zu trennen durch entsprechende Fitfunktionen. Deswegen interessiert mich, ob es neben einer analytisch-exakten auch eine Funktion gibt, die man üblicherweise zur Annäherung benutzen kann und die vielleicht als Standard(fit)funktion in Origin 8.X oder Matlab Curve Fitting Toolbox vorhanden ist.
Viele Grüsse,
Danny
Division 2er Exponentialverteilungen u.ä.
Thema bewerten: 




 • 5 Beiträge
• Seite 1 von 1
• 5 Beiträge
• Seite 1 von 1
Division 2er Exponentialverteilungen u.ä.
- Dateianhänge
-
- Distribtion.png (19.7 KiB) 1571-mal betrachtet
- koda
- Grünschnabel

- Beiträge: 3
- Registriert: Fr 11. Mai 2012, 09:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Division 2er Exponentialverteilungen u.ä.
Hallo,
verstehe ich das richtig, dass die Parameter der Exponentialverteilungen t1,...,tj generell unbekannt sind und durch das Fitten einer entsprechenden Mischverteilung (in diesem Fall ein Exponential Mixture) gefittet werden sollen?
VG
STATWORX
verstehe ich das richtig, dass die Parameter der Exponentialverteilungen t1,...,tj generell unbekannt sind und durch das Fitten einer entsprechenden Mischverteilung (in diesem Fall ein Exponential Mixture) gefittet werden sollen?
VG
STATWORX
- STATWORX
- Foreninhaber

- Beiträge: 85
- Registriert: Di 14. Jun 2011, 19:45
- Danke gegeben: 0
- Danke bekommen: 18 mal in 18 Posts
Re: Division 2er Exponentialverteilungen u.ä.
Ja t_i and t_j sind Zufallszahlen (im realen Sinne von Verweilzeiten), die exponential und nicht normal- oder gleich-verteilt sind (mittels Zufallszahlengenerator).
Die Verteilungen die sich ergeben sollen gefittet werden:
für i_max=1 weiss ich dass sich eine Verteilung ~1/(z+1)^2 ergeben soll von einem Mathe-Doktoranden (mit z = l1t1/(l2t2)). Für i_max>1 ist es eine andere analytische Funktion, die vermutlich etwas mit der Gammaverteilung zu tun hat.
Die Idee ist am Ende an experimentellen Daten eben jene analytische Funktion anzupassen die sich bei einem bestimmten i_max ergibt oder anders: i_max beeinflusst ja die Breite/Form der Verteilung und müsste sich als Parameter der Verteilungsfunktion widerspiegeln und man könnte das als fixen Parameter in der Anpassfunktion berücksichtigen. Am Ende möchte man den <K>-Wert aus dem Fit erhalten. i_max ist meist aber <10 und die Gaussverteilung somit nicht die optimale Anpassfunktion.
In den experimentellen Daten könnte es auch dazu kommen, dass sich 2 Verteilungen überlagern, dann würde man aus der einfachen Fitfunktion eben additiv die neue Fitfunktion erstellen und bekäme 2 <K> Werte (und deren Amplituden) heraus. Beantwortet das deine Frage?
Und danke für die Hilfe,
Danny
Die Verteilungen die sich ergeben sollen gefittet werden:
für i_max=1 weiss ich dass sich eine Verteilung ~1/(z+1)^2 ergeben soll von einem Mathe-Doktoranden (mit z = l1t1/(l2t2)). Für i_max>1 ist es eine andere analytische Funktion, die vermutlich etwas mit der Gammaverteilung zu tun hat.
Die Idee ist am Ende an experimentellen Daten eben jene analytische Funktion anzupassen die sich bei einem bestimmten i_max ergibt oder anders: i_max beeinflusst ja die Breite/Form der Verteilung und müsste sich als Parameter der Verteilungsfunktion widerspiegeln und man könnte das als fixen Parameter in der Anpassfunktion berücksichtigen. Am Ende möchte man den <K>-Wert aus dem Fit erhalten. i_max ist meist aber <10 und die Gaussverteilung somit nicht die optimale Anpassfunktion.
In den experimentellen Daten könnte es auch dazu kommen, dass sich 2 Verteilungen überlagern, dann würde man aus der einfachen Fitfunktion eben additiv die neue Fitfunktion erstellen und bekäme 2 <K> Werte (und deren Amplituden) heraus. Beantwortet das deine Frage?
Und danke für die Hilfe,
Danny
- koda
- Grünschnabel

- Beiträge: 3
- Registriert: Fr 11. Mai 2012, 09:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Division 2er Exponentialverteilungen u.ä.
Hallo,
ich bin etwas verwirrt: in Deinem MATLAB-Code gibt, iMax die Stichprobengröße der zu simulierenden Exponentialverteilung an. Heißt das also, dass Deine Datenbasis, iMax, üblicherweise sehr viel kleiner ist als 10? In diesem Falle dürfte es äußerst schwierig werden, entsprechende Parameter einer wie auch immer gearteten Verteilung zu fitten. Zudem wirst Du hierfür kaum eine analytische Lösung finden, da Parameter komplexer Verteilungen meistens numerisch bestimmt werden.
Wenn Dich am Ende "nur" K interessiert und die Form der beiden Exponentialverteilungen egal ist, könntest Du jede beliebige Verteilung an Deine experimentellen Daten fitten, die flexibel genug ist, verschiedene Schiefen (je nach iMax) abzubilden (z.B. Beta-oder Gamma-Verteilung).
Alternativ, falls Du an den Parametern der Exponentialverteilungen interessiert bist, musst Du eine Likelihood-Funktion für Deine Formel K = t1 / t2 mit t1 und t2 Exponentialdichtefunktionen mit unbekanntem (aber scheinbar gleichem(?) Mittelwert) formulieren und diese in MATLAB numerisch schätzen. Hierfür bietet MATLAB entsprechende Routinen.
VG
STATWORX
ich bin etwas verwirrt: in Deinem MATLAB-Code gibt, iMax die Stichprobengröße der zu simulierenden Exponentialverteilung an. Heißt das also, dass Deine Datenbasis, iMax, üblicherweise sehr viel kleiner ist als 10? In diesem Falle dürfte es äußerst schwierig werden, entsprechende Parameter einer wie auch immer gearteten Verteilung zu fitten. Zudem wirst Du hierfür kaum eine analytische Lösung finden, da Parameter komplexer Verteilungen meistens numerisch bestimmt werden.
Wenn Dich am Ende "nur" K interessiert und die Form der beiden Exponentialverteilungen egal ist, könntest Du jede beliebige Verteilung an Deine experimentellen Daten fitten, die flexibel genug ist, verschiedene Schiefen (je nach iMax) abzubilden (z.B. Beta-oder Gamma-Verteilung).
Alternativ, falls Du an den Parametern der Exponentialverteilungen interessiert bist, musst Du eine Likelihood-Funktion für Deine Formel K = t1 / t2 mit t1 und t2 Exponentialdichtefunktionen mit unbekanntem (aber scheinbar gleichem(?) Mittelwert) formulieren und diese in MATLAB numerisch schätzen. Hierfür bietet MATLAB entsprechende Routinen.
VG
STATWORX
- STATWORX
- Foreninhaber

- Beiträge: 85
- Registriert: Di 14. Jun 2011, 19:45
- Danke gegeben: 0
- Danke bekommen: 18 mal in 18 Posts
Re: Division 2er Exponentialverteilungen u.ä.
Hi Statworx, ich habe den folgenden matlab-Code verwendet, um die cumP(K) Verteilungen zu erhalten:
k=0; for i = [1 2 3 4 5 7 10 15 20 30 40 50 60 70 80 90 100] k = k + 1; rand_nr2(:,k) = 40000*sort(mean(random('exp',10,10000,i),2)./mean(random('exp',10,10000,i),2));
Es ist mir klar, dass ich beliebige Funktionen anpassen kann um den K-Wert (Wendepunkt) und p (Anstieg/Steilheit) zu erhalten. Die mono-exponentiell verteilten t1 und t2 interessieren mich erstmal nicht, sondern nur das K. <t1> und <t2> sind bei mir gleich 10, das stimmt. Aber möchte eben wissen ob es für K eine analytisch exakte Funktion gibt oder einen Ansatz, welcher dann meinetwegen nur numerisch lösbar ist.
Als Teilschritt muss man erstmal die Frage beantworten: z.B. wenn t1 = (t1,1 +t1,2)/2 also der Mittelwert 2er mono-exponentiell verteilter zeiten ist und ich 10000 solcher wertepaare kreiere und anschliessen die 10000 t1 werte zu einem histogramm zusammenfasse, welche funktion diese verteilung analytisch beschreibt und welchen effekt es hat wenn man den mittelwert aus mehr als 2 werten berechnet.
der 2. teilschritt ist ob die division 2er gleichartiger verteilungen dann wieder analytisch beschreibbar ist.
Ich möchte deine Geduld nicht überstrapazieren, aber falls dich das Thema doch genauer interessiert und du Zugang zu elektronischen Journalen hast, schau mal in folgenden Artikel: http://www.sciencedirect.com/science/ar ... 9510005473
Das problem ist anderer natur, aber die erhaltenen Funktionen sehen ähnlich aus und auch die Grundannahmen. eine ähnliche problematik hat man bei der o.g. 1. teilfragestellung
Dort sind bereits die Verweilzeiten tau nicht mehr monoexponentiell verteilt, weil die die Annahmen machen dass tau sich aus mindestens n (unsichtbaren) Verweilzeiten zu einem scheinbaren tau = t1+t2 + ...+ tn aufzummieren. (Bei mir ist es eben der mittelwert statt der summe). Dieses tau ist dann nicht mehr mono-exponentiell verteilt, obwohl die nicht sichtbaren teilverweilzeiten ti mono-exponentiell verteilt waren.
Viele Grüsse, Danny
k=0; for i = [1 2 3 4 5 7 10 15 20 30 40 50 60 70 80 90 100] k = k + 1; rand_nr2(:,k) = 40000*sort(mean(random('exp',10,10000,i),2)./mean(random('exp',10,10000,i),2));
Es ist mir klar, dass ich beliebige Funktionen anpassen kann um den K-Wert (Wendepunkt) und p (Anstieg/Steilheit) zu erhalten. Die mono-exponentiell verteilten t1 und t2 interessieren mich erstmal nicht, sondern nur das K. <t1> und <t2> sind bei mir gleich 10, das stimmt. Aber möchte eben wissen ob es für K eine analytisch exakte Funktion gibt oder einen Ansatz, welcher dann meinetwegen nur numerisch lösbar ist.
Als Teilschritt muss man erstmal die Frage beantworten: z.B. wenn t1 = (t1,1 +t1,2)/2 also der Mittelwert 2er mono-exponentiell verteilter zeiten ist und ich 10000 solcher wertepaare kreiere und anschliessen die 10000 t1 werte zu einem histogramm zusammenfasse, welche funktion diese verteilung analytisch beschreibt und welchen effekt es hat wenn man den mittelwert aus mehr als 2 werten berechnet.
der 2. teilschritt ist ob die division 2er gleichartiger verteilungen dann wieder analytisch beschreibbar ist.
Ich möchte deine Geduld nicht überstrapazieren, aber falls dich das Thema doch genauer interessiert und du Zugang zu elektronischen Journalen hast, schau mal in folgenden Artikel: http://www.sciencedirect.com/science/ar ... 9510005473
Das problem ist anderer natur, aber die erhaltenen Funktionen sehen ähnlich aus und auch die Grundannahmen. eine ähnliche problematik hat man bei der o.g. 1. teilfragestellung
Dort sind bereits die Verweilzeiten tau nicht mehr monoexponentiell verteilt, weil die die Annahmen machen dass tau sich aus mindestens n (unsichtbaren) Verweilzeiten zu einem scheinbaren tau = t1+t2 + ...+ tn aufzummieren. (Bei mir ist es eben der mittelwert statt der summe). Dieses tau ist dann nicht mehr mono-exponentiell verteilt, obwohl die nicht sichtbaren teilverweilzeiten ti mono-exponentiell verteilt waren.
Viele Grüsse, Danny
- koda
- Grünschnabel

- Beiträge: 3
- Registriert: Fr 11. Mai 2012, 09:31
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 5 Beiträge
• Seite 1 von 1
• 5 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 5 Gäste