Hallo zusammen,
das ist mein erster Beitrag und eventuell befinde Ich mich auch schon direkt auf dem Holzweg.
Ich habe in einer Stichprobe von 600 Probanden eine potenzielle Subkohorte von 200 in meine Versuchsreihe einschließen können.
Asl Zielparameter wird ausgerechnet, bei wie vielen dieser Patienten eine Therapie erfolgreich abgeschlossen werden konnte. Das waren in der Subkohorte 50% also 100 der 200.
Nun möchte Ich ein Konfidenzintervalll des N für diese Erfolgsquote ausrechnen, wenn folgende Parameter variieren.
Diese zweite Gruppe umfasst viermal so viele Probanden 2400, Ziel wäre es dass mindestens 10% davon die Therapie erfolgreich abgeschlossen haben.
Also kurz Zusammengefasst:
Bekannte Parameter:
Gesamtheit 1: 600, Rekrutierungsquote für Subkohorte 30%: 200, Davon erfolgreich therapiert 50%: 100
Neue Kohorte:
Gesamtheit 2: 2400, Rekrutierungsquote für Subkohorte 30%: 480, Davon vermutlich erfolgreich therapiert: 240
Kann ich denn für die zweite Annahme in Relation zur 1. Kohorte nun Berechnungen durchführen?
Sorry falls es etwas cahotisch konzipiert ist, vielen Dank
Konfidenzintervall bei rel Häüfigkeiten
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
- nash13
- Grünschnabel

- Beiträge: 5
- Registriert: Mi 12. Mai 2021, 11:35
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Konfidenzintervall bei rel Häüfigkeiten
Hallo Nash,
Das 95%-Konfidenzintervall für den Anteil der erfolgreich abgeschlossenen Therapien lässt sich auf verschiedene Arten bestimmen. Ich rechne meine Statistiken in R, deshalb würde ich das so machen:
Demnach reicht das 95%-Konfidenzintervall für den Anteil der positiven Fälle von 42,8% bis 57,1%.
Den Rest Deiner Frage verstehe ich nicht. Wie das Konfidenzintervall läge wenn man etwas beobachtet hätte was man nicht beobachtet hat ist schwer zu sagen. Vielleicht wird alles viel verständlicher, wenn Du mal ein oder zwei Abstraktionsebenen herunterschaltest und berichtest, was Du eigentlich vorhast, welches Problem im echten Leben Du angehen möchtest. Gerne in einfachem Deutsch und es müssen auch keine statistischen Fachbegriffe drin sein, wenn Du Dir mit denen etwas unsicher sein solltest.
LG,
Bernhard
nash13 hat geschrieben:Asl Zielparameter wird ausgerechnet, bei wie vielen dieser Patienten eine Therapie erfolgreich abgeschlossen werden konnte. Das waren in der Subkohorte 50% also 100 der 200.
Nun möchte Ich ein Konfidenzintervalll des N für diese Erfolgsquote ausrechnen,...
Das 95%-Konfidenzintervall für den Anteil der erfolgreich abgeschlossenen Therapien lässt sich auf verschiedene Arten bestimmen. Ich rechne meine Statistiken in R, deshalb würde ich das so machen:
- Code: Alles auswählen
> binom.test(100, 200)$conf.int
[1] 0.4286584 0.5713416
Demnach reicht das 95%-Konfidenzintervall für den Anteil der positiven Fälle von 42,8% bis 57,1%.
Den Rest Deiner Frage verstehe ich nicht. Wie das Konfidenzintervall läge wenn man etwas beobachtet hätte was man nicht beobachtet hat ist schwer zu sagen. Vielleicht wird alles viel verständlicher, wenn Du mal ein oder zwei Abstraktionsebenen herunterschaltest und berichtest, was Du eigentlich vorhast, welches Problem im echten Leben Du angehen möchtest. Gerne in einfachem Deutsch und es müssen auch keine statistischen Fachbegriffe drin sein, wenn Du Dir mit denen etwas unsicher sein solltest.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5947
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Konfidenzintervall bei rel Häüfigkeiten
Hallo bele,
zunächst vielen Dank für deine hilfreiche Antwort.
Ich hatte schon befürchtet, dass meine Darstellung zu konfus erscheint.
Allgemein gesprochen geht es darum, dass die Anteile der ersten Kohorte bekannt sind, die der zweiten aber fiktiv und nicht getestet.
Wie wahrscheinlich ist es, dass 240 der 2400 aus Gruppe 2 erfolgreich therapiert werden, wenn bei Gruppe 1 es 100 von 600 waren?
zunächst vielen Dank für deine hilfreiche Antwort.
Ich hatte schon befürchtet, dass meine Darstellung zu konfus erscheint.
Allgemein gesprochen geht es darum, dass die Anteile der ersten Kohorte bekannt sind, die der zweiten aber fiktiv und nicht getestet.
Wie wahrscheinlich ist es, dass 240 der 2400 aus Gruppe 2 erfolgreich therapiert werden, wenn bei Gruppe 1 es 100 von 600 waren?
- nash13
- Grünschnabel

- Beiträge: 5
- Registriert: Mi 12. Mai 2021, 11:35
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Konfidenzintervall bei rel Häüfigkeiten
Hallo nash,
bitte formuliere präzise, damit hilfsbereite hier im Forum nur nach der Lösung suchen, die Dich auch interessiert und nicht Zeit und Mühe in eine Lösung stecken, die dann nicht passt.
Sind es in der ersten Kohorte genau 100 von 200? Oder waren es 100 von 600? Geht es darum, ob in der zweiten Kohorte genau 240 von 480 werden oder mindestens 10% von 2400 oder genau 240 aus 2400? Ist der Anteil in der ersten Kohorte bekannt oder muss er aus einer Stichprobe geschätzt werden? Das kann man alles im bisher geschriebenen finden und das geht nicht zusammen. Außerdem muss noch geklärt werden, ob die 600 Teil der 2400 sind oder ob das unanhängige Stichproben sind.
Dann solltest Du Dir Mühe geben, die Darstellung un-konfus zu formulieren und vielleicht meinen Ratschlag befolgen, nicht allgemein zu sprechen sondern ganz konkret das Problem zu schildern. Letzteres ist nicht notwendig, aus vielen Jahren Forumserfahrung aber am erfolgversprechendsten.
LG,
Bernhard
LG,
Bernhard
bitte formuliere präzise, damit hilfsbereite hier im Forum nur nach der Lösung suchen, die Dich auch interessiert und nicht Zeit und Mühe in eine Lösung stecken, die dann nicht passt.
Sind es in der ersten Kohorte genau 100 von 200? Oder waren es 100 von 600? Geht es darum, ob in der zweiten Kohorte genau 240 von 480 werden oder mindestens 10% von 2400 oder genau 240 aus 2400? Ist der Anteil in der ersten Kohorte bekannt oder muss er aus einer Stichprobe geschätzt werden? Das kann man alles im bisher geschriebenen finden und das geht nicht zusammen. Außerdem muss noch geklärt werden, ob die 600 Teil der 2400 sind oder ob das unanhängige Stichproben sind.
nash13 hat geschrieben:Ich hatte schon befürchtet, dass meine Darstellung zu konfus erscheint.
Allgemein gesprochen ...
Dann solltest Du Dir Mühe geben, die Darstellung un-konfus zu formulieren und vielleicht meinen Ratschlag befolgen, nicht allgemein zu sprechen sondern ganz konkret das Problem zu schildern. Letzteres ist nicht notwendig, aus vielen Jahren Forumserfahrung aber am erfolgversprechendsten.
LG,
Bernhard
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5947
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Konfidenzintervall bei rel Häüfigkeiten
Hallo Bernhard,
da hast du natürlich Recht. Man sollte einerseits Äpfel und Birnen nicht vertauschen und zweitens das Problem präzise, aber auch verständlich schildern.
Nun noch ein Mal der Versuch es zu präzisieren.
Erste Kohorte sind bekannte Parameter.
600 werden eingeschlossen davon qualifizieren sich 200 für die Medikamentenstudie und 100 sind erfolgreich therapiert.
Aus Kohorte 2 kennen wir nurdie Anzahl derer, die primär rekrutiert werden 2400 analog zu den 600 aus Gruppe 1.
Wie kann ich jetzt berechnen wie viele Patienten sich qualifizieren und welche davon erfolgreich therapiert werden?
Ich hatte an eine Aussage gedacht in folgender Form:
Mit einem CI von 95% liegt der Rekrutierungsbereich bei (445-515) und die Anzahl der erfolgreich therapierten Patienten bei (87-113). (fiktive Werte von mir gewählt)
Ist so etwas überhaupt in diesem Fall zulässig? Ist dann so eine Verschachtelung zu vernachlässigen? Oder geht man besser auf die "höhere" Ebene und sagt "Im Endeffekt wurden 100 von 600 erfolgreich therapiert, wie ist es nun bei 2400 Patienten?"
Vielen Dank nochmals.
da hast du natürlich Recht. Man sollte einerseits Äpfel und Birnen nicht vertauschen und zweitens das Problem präzise, aber auch verständlich schildern.
Nun noch ein Mal der Versuch es zu präzisieren.
Erste Kohorte sind bekannte Parameter.
600 werden eingeschlossen davon qualifizieren sich 200 für die Medikamentenstudie und 100 sind erfolgreich therapiert.
Aus Kohorte 2 kennen wir nurdie Anzahl derer, die primär rekrutiert werden 2400 analog zu den 600 aus Gruppe 1.
Wie kann ich jetzt berechnen wie viele Patienten sich qualifizieren und welche davon erfolgreich therapiert werden?
Ich hatte an eine Aussage gedacht in folgender Form:
Mit einem CI von 95% liegt der Rekrutierungsbereich bei (445-515) und die Anzahl der erfolgreich therapierten Patienten bei (87-113). (fiktive Werte von mir gewählt)
Ist so etwas überhaupt in diesem Fall zulässig? Ist dann so eine Verschachtelung zu vernachlässigen? Oder geht man besser auf die "höhere" Ebene und sagt "Im Endeffekt wurden 100 von 600 erfolgreich therapiert, wie ist es nun bei 2400 Patienten?"
Vielen Dank nochmals.
- nash13
- Grünschnabel

- Beiträge: 5
- Registriert: Mi 12. Mai 2021, 11:35
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Konfidenzintervall bei relativen Häufigkeiten
Hallo nash,
ich würde das als zwei verschiedene Binomialprozesse verstehen. Jeder gescreente (600 bzw 2400) hat eine Wahrscheinlichkeit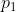 in eine Medikamentenstudie zu kommen und jeder in die Medikamentenstudie gekommene hat eine Wahrscheinlichkeit
in eine Medikamentenstudie zu kommen und jeder in die Medikamentenstudie gekommene hat eine Wahrscheinlichkeit 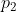 dass er auf das Medikament anspricht.
dass er auf das Medikament anspricht.
Machen wir erst den ersten Schritt: Wenn von 600 gescreenten 200 eingeschlossen werden, dann ist das 1/3. Die wahre Wahrscheinlichkeit kann aber auch ein wenig darüber oder ein wenig darunter liegen. Welche Wahrscheinlichkeit jetzt wie plausibel ist hängt ein wenig von Deinen Vorabannahmen ab, aber sagen wir ganz grob, die Wahrscheinlichkeitsverteilung von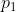 entspricht einer Beta-Verteilung mit den Lageparametern 200 und 400. Blöderweise kann man hier im Forum keine Grafiken hochladen. Ich empfehle Dir, Dir das Programm R von http://www.r-project.org herunterzuladen und zu installieren. Die Wahrscheinlichkeitsdichte von
entspricht einer Beta-Verteilung mit den Lageparametern 200 und 400. Blöderweise kann man hier im Forum keine Grafiken hochladen. Ich empfehle Dir, Dir das Programm R von http://www.r-project.org herunterzuladen und zu installieren. Die Wahrscheinlichkeitsdichte von 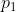 kannst Du Dir dort zeichnen lassen, indem Du folgendes Kommando in R kopierst:
kannst Du Dir dort zeichnen lassen, indem Du folgendes Kommando in R kopierst:
Das 5. und das 95. Perzentil dieser Verteilung:
Man kann sagen, dass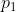 zu 90% zwischen 30.2% und 38,5% liegt. Jetzt ziehen wir uns aus der Wahrscheinlichkeitsverteilung zehntausend plausible Werte
zu 90% zwischen 30.2% und 38,5% liegt. Jetzt ziehen wir uns aus der Wahrscheinlichkeitsverteilung zehntausend plausible Werte  und simulieren damit zehntausend mal, wieviele von 2400 in die Medikamentenstudie einbezogen worden wären, wenn Fortuna frei spielt:
und simulieren damit zehntausend mal, wieviele von 2400 in die Medikamentenstudie einbezogen worden wären, wenn Fortuna frei spielt:
Auch hier gilt: Wenn Du das in R kopierst werden verschiedene Grafiken erstellt und es gibt eine Ausgabe in der Art wie
Also erwarten wir zu 90%, dass von den 2400 zwischen 716 und 886 in die Medikamentenstudie eingeschlossen werden können (ok, das ging zu schnell. Eigentlich solltest Du die Zahl zehntausend etwas erhöhen und das mehrmals laufen lassen um ein Gefühl dafür zu bekommen, wie reproduzierbar diese Simulationsrechnung ist bzw. ob die Zahl der Wiederholungen für Deine Zwecke ausreicht).
Im nächsten Schritt müsste man jetzt mit den zehntausend (oder mehr) Eingeschlossenenzahlen und den möglichen Wahrscheinlichkeiten von der Therapie zu profitieren weiter simulieren. Dafür will ich aber erstmal hören, ob das für Dich so nachvollziehbar ist, ob R als Beschreibungssprache infrage kommt, kurz, ob es Sinn hat, so weiter zu machen.
Im wirklichen Leben werden die Unsicherheiten immer noch größer sein, weil man es nicht schafft, die 2400 Teilnehmer aus de identischen Grundgesamtheit wie die 600 zu rekrutieren. Irgendwas ist bei denen immer anders und daher reicht es vielleicht auch zu sagen: Wir rechnen mit den 716 Einschlüssen weiter, die wir auch im ungünstigen Fall aus den 2400 noch erwarten dürfen.
LG,
Bernhard
ich würde das als zwei verschiedene Binomialprozesse verstehen. Jeder gescreente (600 bzw 2400) hat eine Wahrscheinlichkeit
Machen wir erst den ersten Schritt: Wenn von 600 gescreenten 200 eingeschlossen werden, dann ist das 1/3. Die wahre Wahrscheinlichkeit kann aber auch ein wenig darüber oder ein wenig darunter liegen. Welche Wahrscheinlichkeit jetzt wie plausibel ist hängt ein wenig von Deinen Vorabannahmen ab, aber sagen wir ganz grob, die Wahrscheinlichkeitsverteilung von
- Code: Alles auswählen
curve(dbeta(x, 200, 400), xlab = expression(p[1]), ylab = "Wahrscheinlichkeitsdichte")
Das 5. und das 95. Perzentil dieser Verteilung:
- Code: Alles auswählen
> qbeta(c(.05, .95), 200, 400)
[1] 0.3020199 0.3652790
Man kann sagen, dass
- Code: Alles auswählen
# zehntausend Werte p1
p1 <- rbeta(10000, 200, 400)
plot(density(p1))
# zehntausend mal wird jetzt 2400mal gewürfelt und
# gezählt, wie oft "Einschluss" fällt:
inc <- sapply(p1,
function(p) sum(sample(c(1,0), 2400, TRUE, prob = c(p, 1-p))))
hist(inc)
# jetzt suchen wir wieder das 5. und das 95. Quantil dieser Würfelwerte
quantile(inc, c(.05, .95))
Auch hier gilt: Wenn Du das in R kopierst werden verschiedene Grafiken erstellt und es gibt eine Ausgabe in der Art wie
- Code: Alles auswählen
> quantile(inc, c(.05, .95))
5% 95%
716 886
Also erwarten wir zu 90%, dass von den 2400 zwischen 716 und 886 in die Medikamentenstudie eingeschlossen werden können (ok, das ging zu schnell. Eigentlich solltest Du die Zahl zehntausend etwas erhöhen und das mehrmals laufen lassen um ein Gefühl dafür zu bekommen, wie reproduzierbar diese Simulationsrechnung ist bzw. ob die Zahl der Wiederholungen für Deine Zwecke ausreicht).
Im nächsten Schritt müsste man jetzt mit den zehntausend (oder mehr) Eingeschlossenenzahlen und den möglichen Wahrscheinlichkeiten von der Therapie zu profitieren weiter simulieren. Dafür will ich aber erstmal hören, ob das für Dich so nachvollziehbar ist, ob R als Beschreibungssprache infrage kommt, kurz, ob es Sinn hat, so weiter zu machen.
Im wirklichen Leben werden die Unsicherheiten immer noch größer sein, weil man es nicht schafft, die 2400 Teilnehmer aus de identischen Grundgesamtheit wie die 600 zu rekrutieren. Irgendwas ist bei denen immer anders und daher reicht es vielleicht auch zu sagen: Wir rechnen mit den 716 Einschlüssen weiter, die wir auch im ungünstigen Fall aus den 2400 noch erwarten dürfen.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5947
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Konfidenzintervall bei rel Häüfigkeiten
Hallo Bernhard,
vielen Dank für die ausführliche und sehr gut aufgearbeitete Problemstellung.
Ich schaue mir das im Detail heute an und glaube, dass damit meine eigentliche Frage beantwortet sein dürfte.
Ein schönes Wochenende.
vielen Dank für die ausführliche und sehr gut aufgearbeitete Problemstellung.
Ich schaue mir das im Detail heute an und glaube, dass damit meine eigentliche Frage beantwortet sein dürfte.
Ein schönes Wochenende.
- nash13
- Grünschnabel

- Beiträge: 5
- Registriert: Mi 12. Mai 2021, 11:35
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 7 Beiträge
• Seite 1 von 1
• 7 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 1 Gast


