STATISTIK-FORUM.de

[ahundler]

Hallo liebe Community,

ich möchte eine einfache lineare Regression durchführen, wozu ich ja die folgenden Modellannahmen überprüfen muss:

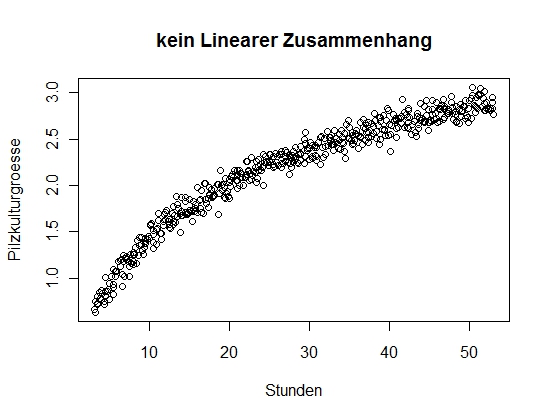
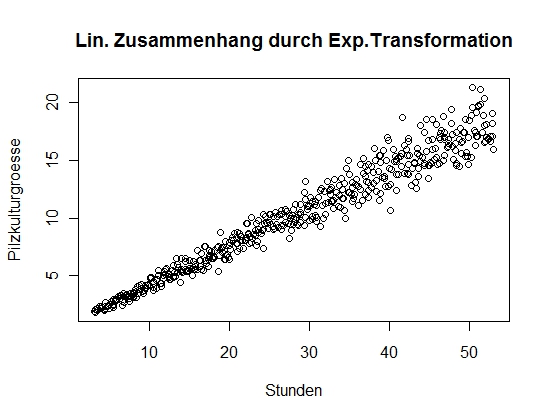
1. Linearität
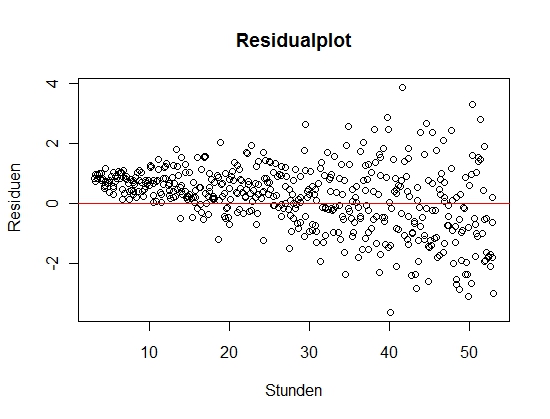
2. Homoskedastizität
3. Normalität

Meine erste Frage: gibt es gute Literaturhinweise, wo ich die Überprüfung dieser Modellannahmen in SPSS nachschauen kann?

Außerdem hätte ich bereits eine Frage zur Überprüfung der Linearität: Ich verstehe nicht, was es mit dem studentisierten ausgeschlossenenen Residuen auf sich hat.

Ich habe gelesen, dass man mit der abhängigen Variable auf der X-Achse und den studentisierten ausgeschlossenenen Residuen auf der Y-Achse anhand eines Diagramms die Linearität überprüfen kann. Inhaltlich kann ich aber leider nicht nachvollziehen, wieso man so vorgeht...


Ich wäre sehr dankbar, wenn ihr mir helfen könntet! Ich bin leider noch eine Einsteiger im Gebiet der Statistik, deswegen hoffe ich auf verständliche Erklärungen...

[Streuner]

Hey ahnundler,

mit SPSS kenn ich mich leider nicht aus, da ich meist mittels R arbeite.

Zu deinen aufgeführten Punkten 1. und 3. kann ich dir ein Beispiel zeigen (siehe Grafiken unten)

Wie du zu 1. schon sagtest, kann man Linearität grafisch daran überprüfen, ob (wie der Name schon sagt) ein linerar Zusammenhang zwischen deiner abhängigen Variablen y und deiner unabhängigen Variablen x besteht.

Rplot03.jpeg (66.62 KiB) 7195-mal betrachtet

Falls dies, wie in der Grafik, nicht der Fall ist kann man die Daten so transformieren, dass sich ein lin. Zusammenhang einstellt

Rplot.jpeg (73.04 KiB) 7195-mal betrachtet

Deinen Punkt 3. kann man ebenfalls grafisch überprüfen, indem man sich den Residualplot anschaut, und überprüft ob man eine Struktur in den Fehlern erkännt.

Rplot01.jpeg (87.47 KiB) 7195-mal betrachtet

Hier erkennt man eine klare Struktur in den Fehlern (erster Teil konsequent über der Null-Linie im weiteren verlauf stellt sich eine symmetrische Fehlerverteilung um 0 ein), daher kann man schließen, dass die Fehler nicht normalverteilt sind.


Zu 2. kann ich dir leider so spontan nichts sagen, aber da findet sich bestimmt noch jemand für.


Hoffe ich konnte dir soweit erstmal etwas Klarheit verschaffen.


Mit freundlichen Grüßen,

M.

[ahundler]

Vielen Dank schonmal soweit!!

Ich habe zur Überprüfung der Linearität auch schon eine "augenscheinliche" Prüfung vorgenommen. Aber ich habe gelesen, dass dies nicht ausreichend ist und man deswegen auch eine Prüfung anhand der studentisierten Residuen vornehmen soll...

Und wie ich das verstanden habe macht man eine solche Überprüfung auch für jede Variable einzeln- ist das richtig? Das macht für mich irgendwie garkeinen Sinn...

Kann mir jemand dieses Konzept vielleicht erklären- oder mir wie gesagt zu der gesamten Thematik einen guten Literaturtipp nennen?

[Berry]

Hallo ahundler.

Unter

Und wie ich das verstanden habe macht man eine solche Überprüfung auch für jede Variable einzeln- ist das richtig? Das macht für mich irgendwie garkeinen Sinn...

verstehe ich, dass es sich nicht um eine einfache sondern eine multiple Regression handelt. In diesem Fall musst Du den Component+Residuals-Plot verwenden, in dem die partiellen Residuen der einzelnen (metrischen!) Variablen gegen diese Variablen abgetragen sind.

Hier evtl. ein Literaturhinweis: "Regression..." von Fahrmeir. Ich habe die genaue Buchbezeichnung leider nicht zur Hand, aber wenn Du so googelst, müsstest Du es auch finden.

Sollte es sich doch um einfache Regression handeln, dann auch die einfachen Residuen gegen die (einzige) Variable plotten.

[Streuner]

Nabend zusammen,

ich weiß, dass Thema ist schon was älter und soweit auch beantwortet worden, aber ich wollte noch etwas ergänzen, was dem einem oder anderem vielleicht weiterhilft, der nach dieser Thematik sucht:

Für die Überprüfung der Modellannahmen gibt es statistische Tests auf die ich im folgenden nur verweise, aber nicht genauer eingehe (bei Bedarf bitte selbst in der Literatur nachschlagen):

Bei den Tests geht es in erster Linie um die Modellannahme, dass die Fehler Normalverteilt sind, dies kann sich in 2 Themen splitten lassen:
- Heteroskedastizität und
- Autokorrellation.

Heteroskedastizität oder der gegenteilige Begriff Homoskedastizität sind Begriffe, welche die Streuung innerhalb der Daten charakterisiert ; hier zu nennen sind:
White-, Breusch-Pagan-,Goldfeld-Quandt-Test

Bei Autokorrellation, wie der Name schon sagt, handelt es sich um die Korrelation der Störgrößen, diese sollten im Regressionsmodell unkorreliert sein ; hier zu nennen sind:
Durbin-Watson-, Box-Pierce-,Ljung-Box-Test


Hoffe dies kann einigen, die vielleicht per Suchfunktion auf dieses Thema stoßen, helfen.



Mit freundlichen Grüßen,

M.