STATISTIK-FORUM.de

[Tupe]

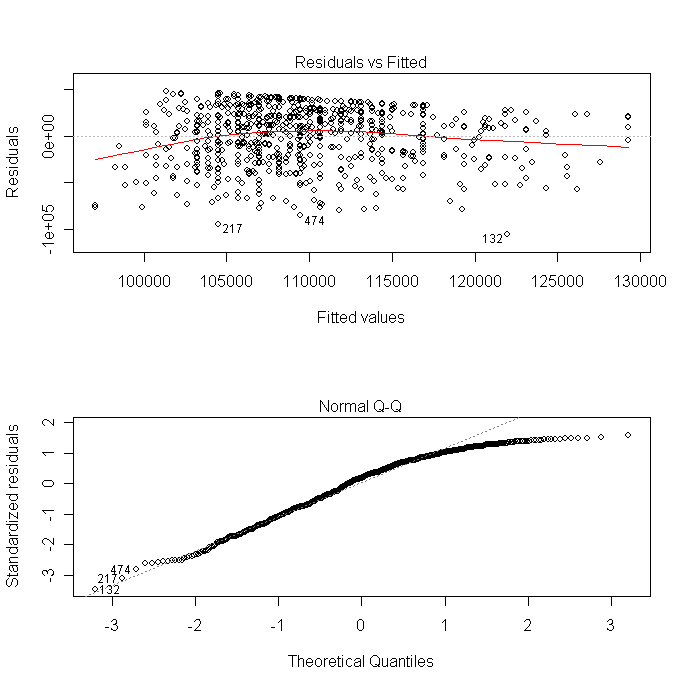
Hallo Leute, hab mal ein paar Fragen... Wir machen jetzt angewandte Statistik und sollten ein lineares Modell schätzen und dann die Residuen ausgeben... Wir haben einen Datensatz über Immobilien und haben uns ein Streudiagram mit dem Preis in abhängigkeit von der Wohnfläche angegeben. Ich habe mal eine Datei eingefügt.. ich soll das interpretieren aber weiss garnicht was man da schreiben soll.. bzw. wo man das gut nachlesen kann.. Kann mir da jemand nen Tipp geben was man da zum Beispiel sagen könnte.

[Streuner]

Morgen Tupe,

an einem Residualplot kann man verschiedene Dinge betrachten:

1) Wie gut schätzt dein Model den tatsächlichen Wert. Deine geschätzten Fehler, also Residuen, ergeben sich ja aus der Gleichung:
Zielgröße(y) = Designmatrix(X) * geschätzte Einflussgröße (beta_Dach)

Dabei, wie in deinem Plot richtig eingezeichnet, gibt die Nullgrade die perfekte Anpassung wieder. Du kannst nun betrachten wie weit deine Residuen um die 0 streuen bzw wie sie im Verhältnis zur Nullgraden liegen, was ist die größte Abweichung etc. um Aussagen über die Güte deines Modells zu treffen

2) Kannst du damit die Annahme von (Multi-) normalverteilten Fehlern "testen" (hier gemeint jediglich grafischer teste, es gibt andere richtige Testverfahren dafür).
Ist eine Struktur in den Fehler zu erkennen, so ist die Annahme der normalverteilten Fehler nicht mehr tragbar.

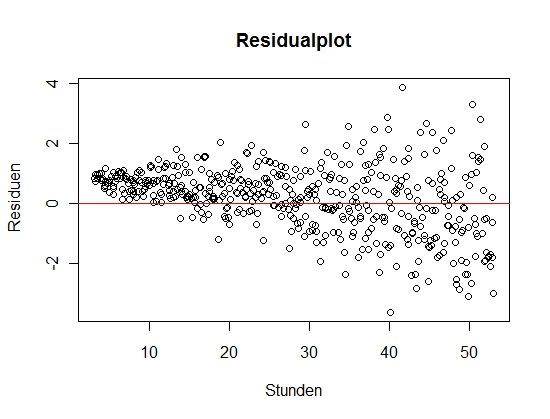
Hier mal ein Plot, wo man recht gut eine Struktur erkennen kann, also eine Verletzung der normalverteilten Fehler annehmen kann.

Rplot01.jpeg (87.47 KiB) 646-mal betrachtet

Mit freundlichen Grüßen,
M