STATISTIK-FORUM.de

[mammut]

Hallo liebe statistik Freunde,

leider, bin ich eine ziemlich lange Zeit aus dem Thema raus und benötige einen Hinweis welchen Test man verwenden sollte.

Es geht um zwei Stichproben (Bezugsstichprobe und Teststichprobe) mit jeweils (x,y)-Werten x und y müssen einen linearen Zusammenhang abbilden. Wenn nicht, dann sind die Daten Schrott und somit die Erhebung nicht brauchbar.

Um den linearen Zusammenhang je Stichprobenreihe zu ermitteln wird eine klassische Regression durchgeführt und anhand des Bestimmtheitsmaß wir festgelegt,
linearer Zusammenhang besteht oder nicht.
Wenn nun beide Stichproben linear sind, muss getestet werden, ob die beiden linearen Funktionen identisch sind (oder besser H0 beide Funktionen sind nicht identisch), und an dieser Stelle habe ich keinen Test gefunden, der augenscheinlich passt.
Daher die freundliche Bitte mir ein Hinweis zu geben welcher Test hier infrage kommt.

Vielen Dank

[PonderStibbons]

Gesamtdatensatz bilden, die beiden Substichproben mit 0 und 1 codieren,
Produkt aus Stichprobenindikator und Prädiktor bilden (repräsentiert die
Wechselwirkung, d.h. ob die Steigung je nach Substichprobe unterschiedlich
ist), Stichprobenindikator und Wechselwirkung in die Gleichung aufnehmen.

Mit freundlichen Grüßen

PonderStibbons

[bele]

Hallo mammut,

in der Regel wird es am einfachsten sein, ein gemeinsames lineares Modell für beide Messungen aufzustellen und eine Dummyvariable einzubeziehen, die Bezugs- und Teststichprobe unterscheidet. Sei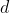 eine Dummyvariable die bei der Bezugsstichprobe Null und bei der Testsichprobe Eins wird. Jetzt rechnen wir ein Modell der Art:


Wenn dann ist das eine einfache lineare Regression. Wenn aber wird, dann steigert sich der Intercept von 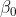auf und die Steigung steigert sich von 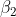auf . Deine Frage reduziert sich sich also darauf, ob 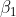und 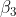jeweils Null sind.

LG,
Bernhard

PS: PonderStibbons war schneller, aber nachdem ich das so ausführlich geschrieben hatte, wollte ich es auch nicht verwerfen.