Guten Morgen,
zur Zeit möchte ich eine Versuchsplanung erstellen, die insgesamt 8 verschiedene Einstellungen benötigt. Da ich jedoch nur mit den klassischen zwei Einstellungen ,,-" und ,,+" vertraut bin, bräuchte ich hier ein Paar Impulse zur Erstellung meiner Versuchsplanung. Zur Übersicht habe ich alle mir bekannten Daten zusammengefasst:
a.) Hypothese:
→ Nanopartikel können durch bestimmte Chemikalien funktionalisiert werden
► Funktionalisierung: die funktionellen Gruppen der Chemikalien können an die Oberfläche der Nanopartikel angedockt werden
► Methode: Mit einem Spektrometer kann die Wellenzahl der funktionellen Gruppen detektiert werden
╚> keine Detektion möglich: Funktionalisierung nicht erfolgreich
╚> Detektion möglich: Funktionalisierung erfolgreich
b.) Zielgröße/Qualitätsmerkmal
→ Abweichung Alpha [%]
► die Abweichung berechnet sich wie folgt:
A = {1 - [v(exp)/v(Ref)]} * 100 %
mit
v(exp): entspricht dem experimentell bestimmten Wert der Wellenzahl
V(Ref): entspricht einem Referenzwert der Wellenzahl (Literatur)
c.) Einstellung
→ es wird das molare Verhältnis zwischen der Chemikalie und den Nanopartikeln verwendet
► 8 Abstufungen:
z.B
0,1:1
0,2:1
etc.
d) Parameter
→ es werden drei Chemikalien (A, B, C) eingesetzt
Problem:
Nach der vollfaktoriellen Methode würde ich ja 3^8 = 6561 Versuchsdurchläufe brauchen. Den Aufwand möchte ich aber selbst mit Softwarelösungen nicht betreiben.
Daher wollte ich wissen, wie man mit den Eingangsdaten sinnvoller umgehen könnte
Wissensstand:
nach Karl Siebert gabs ja bereits das Beispiel mit dem Rasensprenger. Dort wurden drei Variablen mit zwei Einstellungen untersucht.
Aber wie geht man mit Variablen um, die einer Gruppe zugeordnet (3 Chemikalien) und nur in ihren Eigenschaften unterscheidbar sind (molare Masse, Dichte, etc.)?
Mfg
Xalgy
Versuchsplanung mit mehr als zwei Einstellungen erstellen
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
- Xalgy
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 19. Nov 2022, 10:28
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
Hallo Xalgy,
Nur so als kleiner Tipp am Rande, der Forumsbetreiber ermöglicht es uns, hier LaTeX zu benutzen. So kannst Du auch\cdot 100%) schreiben. Spielt erstmal keine Rolle, ist aber nützlich, wenn man als Naturwissenschaftler LaTeX-Formelsatz ein wenig kann und hier ist ein schöner Ort, das zu üben.
schreiben. Spielt erstmal keine Rolle, ist aber nützlich, wenn man als Naturwissenschaftler LaTeX-Formelsatz ein wenig kann und hier ist ein schöner Ort, das zu üben.
Das habe ich nicht verstanden. Du müsstest für jede Chemikalie jede Konzentration ausprobieren. Sind das dann nicht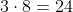 Kombinationen?
Kombinationen?
Muss man das kennen? Die Formulierung legt das nahe aber weder meine Google-Suche nach "Karl Siebert Rasensprenger" noch https://de.wikipedia.org/wiki/Karl_Siebert lösen das auf. Ist das Beispiel weltberühmt bei den Lesern Deines Lehrbuchs?
LG,
Bernhard
die Abweichung berechnet sich wie folgt:
A = {1 - [v(exp)/v(Ref)]} * 100 %
Nur so als kleiner Tipp am Rande, der Forumsbetreiber ermöglicht es uns, hier LaTeX zu benutzen. So kannst Du auch
Nach der vollfaktoriellen Methode würde ich ja 3^8 = 6561 Versuchsdurchläufe brauchen.
Das habe ich nicht verstanden. Du müsstest für jede Chemikalie jede Konzentration ausprobieren. Sind das dann nicht
nach Karl Siebert gabs ja bereits das Beispiel mit dem Rasensprenger.
Muss man das kennen? Die Formulierung legt das nahe aber weder meine Google-Suche nach "Karl Siebert Rasensprenger" noch https://de.wikipedia.org/wiki/Karl_Siebert lösen das auf. Ist das Beispiel weltberühmt bei den Lesern Deines Lehrbuchs?
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
Nochmal Hallo,
Da wird man von einem Chemiker in Erfahrung bringen können, ob man bei einer Zunahme der Konzentration um einen Schritt eher mit einer konstanten Zunahme von rechnen darf oder bei einer Multiplikation der der Konzentration um einen festen Betrag mit einer konstanten Zunahme rechnen darf oder was da so üblicherweise zu erwarten ist. Vielleicht kann ein Chemiker einem auch sagen, ob es realistisch ist, dass Chemikalie A (das ist unglücklich, die genauso zu benennen wie die Zielgröße
rechnen darf oder bei einer Multiplikation der der Konzentration um einen festen Betrag mit einer konstanten Zunahme rechnen darf oder was da so üblicherweise zu erwarten ist. Vielleicht kann ein Chemiker einem auch sagen, ob es realistisch ist, dass Chemikalie A (das ist unglücklich, die genauso zu benennen wie die Zielgröße  ) bei gleicher Konzentration immer ein 2,3fache so hohes
) bei gleicher Konzentration immer ein 2,3fache so hohes  erzielt wie Chemikalie B und ein 0,5 fach so hohes wie Chemikalie C oder welche Art von Zusammenhang da zu erwarten ist.
erzielt wie Chemikalie B und ein 0,5 fach so hohes wie Chemikalie C oder welche Art von Zusammenhang da zu erwarten ist.
Wenn es dazu gute theoretische Annahmen geben sollte, kann man sich überlegen, wie man die in einem statistischen Modell abbilden will. Wenn es keine gute Theorie dazu geben sollte, dann könnte man erstmal die Messreihen durchführen und die Ergebnisse grafisch auftragen bevor man sich überlegt, wie man damit umgehen will. Besonders nützlich ist es für die statistische Modellbildung aber oft, wenn man weiß, welche Fragestellung am Ende mit der Versuchsreihe beantwortet werden soll.
LG,
Bernhard
Xalgy hat geschrieben:Aber wie geht man mit Variablen um, die einer Gruppe zugeordnet (3 Chemikalien) und nur in ihren Eigenschaften unterscheidbar sind (molare Masse, Dichte, etc.)?
Da wird man von einem Chemiker in Erfahrung bringen können, ob man bei einer Zunahme der Konzentration um einen Schritt eher mit einer konstanten Zunahme von
Wenn es dazu gute theoretische Annahmen geben sollte, kann man sich überlegen, wie man die in einem statistischen Modell abbilden will. Wenn es keine gute Theorie dazu geben sollte, dann könnte man erstmal die Messreihen durchführen und die Ergebnisse grafisch auftragen bevor man sich überlegt, wie man damit umgehen will. Besonders nützlich ist es für die statistische Modellbildung aber oft, wenn man weiß, welche Fragestellung am Ende mit der Versuchsreihe beantwortet werden soll.
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
bele hat geschrieben:Hallo Xalgy,die Abweichung berechnet sich wie folgt:
A = {1 - [v(exp)/v(Ref)]} * 100 %
Nur so als kleiner Tipp am Rande, der Forumsbetreiber ermöglicht es uns, hier LaTeX zu benutzen. So kannst Du auchschreiben. Spielt erstmal keine Rolle, ist aber nützlich, wenn man als Naturwissenschaftler LaTeX-Formelsatz ein wenig kann und hier ist ein schöner Ort, das zu üben.
Nach der vollfaktoriellen Methode würde ich ja 3^8 = 6561 Versuchsdurchläufe brauchen.
Das habe ich nicht verstanden. Du müsstest für jede Chemikalie jede Konzentration ausprobieren. Sind das dann nichtKombinationen?
nach Karl Siebert gabs ja bereits das Beispiel mit dem Rasensprenger.
Muss man das kennen? Die Formulierung legt das nahe aber weder meine Google-Suche nach "Karl Siebert Rasensprenger" noch https://de.wikipedia.org/wiki/Karl_Siebert lösen das auf. Ist das Beispiel weltberühmt bei den Lesern Deines Lehrbuchs?
LG,
Bernhard
a.) Literaturverweis
meine Grundlagen zur statistischen Versuchsplanung habe ich aus der folgenden Literatur gezogen:
Siebertz et al., Karl (2010) Statistische Versuchsplanung: Design of Experiments (Vgl. S. 10). Springer. Doi: 10.1007/978-3-642-05493-8
c.) Berechnung der Kombinationen / benötigten Versuchsdurchführung
so wie ich das in Erinnerung habe, muss ich ja die Anzahl der Variablen zur Potenz mal die Anzahl der Stufen (Einstellungen) mit berücksichtigen
(Verweis auf die obiges Literaturbeispiel)
- Xalgy
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 19. Nov 2022, 10:28
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
bele hat geschrieben:Nochmal Hallo,Xalgy hat geschrieben:Aber wie geht man mit Variablen um, die einer Gruppe zugeordnet (3 Chemikalien) und nur in ihren Eigenschaften unterscheidbar sind (molare Masse, Dichte, etc.)?
Da wird man von einem Chemiker in Erfahrung bringen können, ob man bei einer Zunahme der Konzentration um einen Schritt eher mit einer konstanten Zunahme vonrechnen darf oder bei einer Multiplikation der der Konzentration um einen festen Betrag mit einer konstanten Zunahme rechnen darf oder was da so üblicherweise zu erwarten ist. Vielleicht kann ein Chemiker einem auch sagen, ob es realistisch ist, dass Chemikalie A (das ist unglücklich, die genauso zu benennen wie die Zielgröße
) bei gleicher Konzentration immer ein 2,3fache so hohes
erzielt wie Chemikalie B und ein 0,5 fach so hohes wie Chemikalie C oder welche Art von Zusammenhang da zu erwarten ist.
Wenn es dazu gute theoretische Annahmen geben sollte, kann man sich überlegen, wie man die in einem statistischen Modell abbilden will. Wenn es keine gute Theorie dazu geben sollte, dann könnte man erstmal die Messreihen durchführen und die Ergebnisse grafisch auftragen bevor man sich überlegt, wie man damit umgehen will. Besonders nützlich ist es für die statistische Modellbildung aber oft, wenn man weiß, welche Fragestellung am Ende mit der Versuchsreihe beantwortet werden soll.
LG,
Bernhard
Mit der Versuchsreihe möchte ich herausfinden, welche der drei Chemikalien am Besten für eine Funktionalisierung der Nanopartikel-Oberfläche geeignet ist.
Zur Beantwortung dieser Frage möchte ich die FTIR-Spektroskopie heranziehen. Nach meinen Recherchen gibt es bestimmte Wellenzahlen, welche (theoretisch) für den Erfolg jener Funktionalisierung sprechen.
Um die Eignung dieser Chemikalien für eine Funktionalisierung zu überprüfen, möchte ich durch meine funktionalisierten Nanopartikel einen experimentellen Wert der Wellenzahl erheben.
Zur Vergleichbarkeit der Chemikalien untereinander setze ich die experimentellen Wellenzahl in Beziehung mit den theoretischen Wellenzahlen. Diese Beziehung definiere ich als Abweichung des experimentellen Wertes zum theoretischen Wert.
Nach der obigen Formel würde ich im optimalen Fall (beide Werte stimmen überein) eine Abweichung von 0 % erhalten: somit kann ich das jeweilige molare Verhältnis weiterverwenden
Im Kontrast hierzu würde ich im ungünstigen Fall (der experimentelle Wert ist erheblich kleiner als der theoretische Wert) eine Abweichung größer als 99 %: somit könnte ich das molare Verhältnis, welches für diese Abweichung verantwortlich ist, ausschließen.
Die Frage wäre dann eben, wie eine solche Versuchsplanung aussehen könnte, um die Eignung der Chemikalien untereinander vergleichen zu können...
- Xalgy
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 19. Nov 2022, 10:28
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
Hallo Xalgy,
wenn der Herr Siebert jetzt ein z am Ende hat und Siebertz heißt, dann findet man ganz leicht PDFs in denen auch ein Rasensprengerbeispiel super ausführlich behandelt wird. Das Beispiel scheint sich durch verschiedene Kapitel und einen Anhang durchzuziehen, daher müsste man wohl weite Teile des Buches lesen. Auf der angeführten Seite 10 finde ich das Wort Potenz oder sonst irgendeine Rechenanweisung jedenfalls nicht ( https://docplayer.org/83759908-Statisti ... anung.html )
Wenn eine Mischung aus allen drei Chemikalien in je acht verschiedenen Konzentrationen anzurühren wäre, dann würde ich sagen, dass 8^3 = 512 Mischungsverhältnisse erstellt werden können, aber Deine Problembeschreibung liest sich eher so, als ob jeweils nur eine der drei Chemikalien einzusetzen ist, dann bleibe ich bei 8*3. Wie man so auf 3^8 kommen soll bleibt mir unklar.
Soweit die Kombinatorik. Ich behaupte aber nicht, dass ich von DoE viel verstehen würde, daher halte ich mich aus diesem Thread vielleicht besser heraus.
Viel Erfolg noch,
Bernhard
wenn der Herr Siebert jetzt ein z am Ende hat und Siebertz heißt, dann findet man ganz leicht PDFs in denen auch ein Rasensprengerbeispiel super ausführlich behandelt wird. Das Beispiel scheint sich durch verschiedene Kapitel und einen Anhang durchzuziehen, daher müsste man wohl weite Teile des Buches lesen. Auf der angeführten Seite 10 finde ich das Wort Potenz oder sonst irgendeine Rechenanweisung jedenfalls nicht ( https://docplayer.org/83759908-Statisti ... anung.html )
Wenn eine Mischung aus allen drei Chemikalien in je acht verschiedenen Konzentrationen anzurühren wäre, dann würde ich sagen, dass 8^3 = 512 Mischungsverhältnisse erstellt werden können, aber Deine Problembeschreibung liest sich eher so, als ob jeweils nur eine der drei Chemikalien einzusetzen ist, dann bleibe ich bei 8*3. Wie man so auf 3^8 kommen soll bleibt mir unklar.
Soweit die Kombinatorik. Ich behaupte aber nicht, dass ich von DoE viel verstehen würde, daher halte ich mich aus diesem Thread vielleicht besser heraus.
Viel Erfolg noch,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
bele hat geschrieben:Hallo Xalgy,
wenn der Herr Siebert jetzt ein z am Ende hat und Siebertz heißt, dann findet man ganz leicht PDFs in denen auch ein Rasensprengerbeispiel super ausführlich behandelt wird. Das Beispiel scheint sich durch verschiedene Kapitel und einen Anhang durchzuziehen, daher müsste man wohl weite Teile des Buches lesen. Auf der angeführten Seite 10 finde ich das Wort Potenz oder sonst irgendeine Rechenanweisung jedenfalls nicht ( https://docplayer.org/83759908-Statisti ... anung.html )
Wenn eine Mischung aus allen drei Chemikalien in je acht verschiedenen Konzentrationen anzurühren wäre, dann würde ich sagen, dass 8^3 = 512 Mischungsverhältnisse erstellt werden können, aber Deine Problembeschreibung liest sich eher so, als ob jeweils nur eine der drei Chemikalien einzusetzen ist, dann bleibe ich bei 8*3. Wie man so auf 3^8 kommen soll bleibt mir unklar.
Soweit die Kombinatorik. Ich behaupte aber nicht, dass ich von DoE viel verstehen würde, daher halte ich mich aus diesem Thread vielleicht besser heraus.
Viel Erfolg noch,
Bernhard
Vielen Dank schonmal für den Input. Ich selbst bin kein Naturwissenschaftler, welcher sich ausgiebig mit der Grundlagenforschung beschäftigt. Ich bin ein eher praktisch orientierter Ingenieur. Das obige Problem soll mir später beim 3D-Drucken von Keramiken im FDM-Drucker weiterhelfen. Dazu brauche ich ein thermoplastisches Filament, in dem die Partikel (ähnlich einem Verbundwerkstoff) eingebettet und stabil extrudiert werden können. Das hat leider noch nie geklappt. Deswegen habe ich mal einen Chemiker gefragt, wie ich die Haftung der keramischen Partikel zum Thermoplast verbessern kann. Und jetzt versuche ich, seinen Lösungsvorschlag der Funktionalisierung umzusetzen.
Um nochmal auf deinen Vorschlag zu kommen: Mit deinem Ansatz kommst zu auf insgesamt 24 Versuchsdurchläufe (alle Chemikalien soll also mit 8 Stufen getestet werden → jede Versuchsreiche wird unabhängig getestet?)
Nach welchen ,,Kriterien" würdest du diese Versuchsreihen untereinander vergleichen? (Vgl. Punkt b.) im unteren Beispiel)
Ich kenne das Vorgehen nur in der Form (als Beispiel):
a.) Zielgröße/Qualitätsmerkmal
→ elastische Verformungsenergie
► Frage: Welche elastische Verformungsenergie muss beim Aufprall eines Fahrzeugs bereitgestellt werden, ohne dessen Insassen lebensgefährlich zu verletzen?
Ich habe z.B die drei Variablen
X: Geschwindigkeit eines Fahrzeugs
Y: Nutzlast des Fahrzeug (Fahrer, Gepäck, etc.)
Z: Bremsweg
mit den Einstellungen
X: ,,-": Geschwindigkeit (innerorts) und Richtgeschwindigkeit ,,Autobahn"
Y: ,,-": Masse des Fahrers und ,,+" Masse des Fahrers+Gepäck+weitere Insassen
Z: ,,-": Bremsweg im Sommer und ,,+": Bremsweg im Winter
b.) Berechnung der Effektdiagramme und Haupt-Wechselwirkungen
c.) Vergleich der experimentell ermittelten elastischen Verformungsenergien
- Xalgy
- Grünschnabel

- Beiträge: 4
- Registriert: Sa 19. Nov 2022, 10:28
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Versuchsplanung mit mehr als zwei Einstellungen erstelle
Hallo Xalgy,
Ich bin Arzt, der sich hauptsächlich mit Patientenversorgung (also praktisch) und als Freizeitwissenschaftler (also schon beruflich aber eben nur aus Interesse uns Spaß) mit Wissenschaft und Statistik beschäftigt. Meine Kombinatorikkenntnisse stammen noch aus dem Gymnasium, damals war ich ziemlich gut im Matheleistungskurs.
Als Arzt kann ich bei allem, was Du danach geschrieben hast nicht mitreden. Ich war davon ausgegangen, dass Du oben eine Zielgröße definiert hast, die Du optimieren willst. Demnach hätten die Bedingungen "gewonnen", bei denen
definiert hast, die Du optimieren willst. Demnach hätten die Bedingungen "gewonnen", bei denen  möglichst groß (oder klein?) wird. Wenn das nicht so ist, habe ich oben offensichtlich nichts verstanden und dann solltest Du das von mir geschriebene auch nicht allzu ernst nehmen.
möglichst groß (oder klein?) wird. Wenn das nicht so ist, habe ich oben offensichtlich nichts verstanden und dann solltest Du das von mir geschriebene auch nicht allzu ernst nehmen.
LG,
Bernhard
Xalgy hat geschrieben:Ich selbst bin kein Naturwissenschaftler, welcher sich ausgiebig mit der Grundlagenforschung beschäftigt. Ich bin ein eher praktisch orientierter Ingenieur.
Ich bin Arzt, der sich hauptsächlich mit Patientenversorgung (also praktisch) und als Freizeitwissenschaftler (also schon beruflich aber eben nur aus Interesse uns Spaß) mit Wissenschaft und Statistik beschäftigt. Meine Kombinatorikkenntnisse stammen noch aus dem Gymnasium, damals war ich ziemlich gut im Matheleistungskurs.
Nach welchen ,,Kriterien" würdest du diese Versuchsreihen untereinander vergleichen? (Vgl. Punkt b.) im unteren Beispiel)
Als Arzt kann ich bei allem, was Du danach geschrieben hast nicht mitreden. Ich war davon ausgegangen, dass Du oben eine Zielgröße
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Thema bewerten: 




 • 8 Beiträge
• Seite 1 von 1
• 8 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 0 Gäste


