Dear Statistik Forum,
I hope this is the right spot for my problem. I really need some help solving this task, I appreciate every solution/ explanation (you can also answer in German/deutsch I will probably understand!)
Let Y1, . . . , Yn ∼ B(1, π) be an iid sample of Bernoulli random variables with n ≥ 5. Recall that E[Yi] = π and Var[Yi] = π(1 − π).
The following statistics are possible estimators of π:
I cannot upload an image but please find it here
https://www.directupload.net/file/d/674 ... ew_png.htm
1. Which of the proposed estimators for π is unbiased? Which of them is asymptotically unbiased?
2. Compute the variances of ˆπ1, ˆπ2, and ˆπ3.
please do not hesitate to help me
kind regards,
karolin
Bernoulli random variables
Thema bewerten: 




 • 3 Beiträge
• Seite 1 von 1
• 3 Beiträge
• Seite 1 von 1
- karolin25
- Grünschnabel

- Beiträge: 2
- Registriert: So 27. Nov 2022, 14:49
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Re: Bernoulli random variables
Hi karolin,
we do usually ask people with homework questions to present some thoughts or computations of their own in order to better understand, where exactly the problem arises and because we do not see ourselves as a homework solution service.
However, as this is your first post here:
Solution (ii) is the easiest to address: with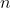 being unknown and all
being unknown and all 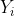 identically distributed, is there any reasoning for a constant of 4 in the denumerator or treating
identically distributed, is there any reasoning for a constant of 4 in the denumerator or treating 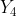 especially? I could not think of any so I feel (ii) is just a distractor item.
especially? I could not think of any so I feel (ii) is just a distractor item.
So it comes down to (i) and (iii). One of them should be an unbiased predictor, the other should turn into an unbiased predictor when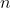 grows towards
grows towards 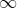 . So that will be a formula where a bias is introduced that is dependent on
. So that will be a formula where a bias is introduced that is dependent on 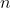 .
.
Now let's approach this in a very simple manner. Imagine you draw cards with either a 0 or a 1 on them. After ten draws you have got three 0`s and seven 1`s. What is your best guess for the percentage of 0`s in the deck? How did you calculate that and which role did the number ten play in that calculation?
Cheers,
Bernhard
PS: for future reference and prevention of link rot: (i) is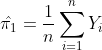 and (iii) is
and (iii) is 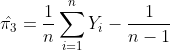
we do usually ask people with homework questions to present some thoughts or computations of their own in order to better understand, where exactly the problem arises and because we do not see ourselves as a homework solution service.
However, as this is your first post here:
Solution (ii) is the easiest to address: with
So it comes down to (i) and (iii). One of them should be an unbiased predictor, the other should turn into an unbiased predictor when
Now let's approach this in a very simple manner. Imagine you draw cards with either a 0 or a 1 on them. After ten draws you have got three 0`s and seven 1`s. What is your best guess for the percentage of 0`s in the deck? How did you calculate that and which role did the number ten play in that calculation?
Cheers,
Bernhard
PS: for future reference and prevention of link rot: (i) is
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5963
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1410 mal in 1396 Posts
Re: Bernoulli random variables
thank you for your help.
I am not quite sure, could you explain what I need to calculate, and especially how?
Best regards
I am not quite sure, could you explain what I need to calculate, and especially how?
Best regards
- karolin25
- Grünschnabel

- Beiträge: 2
- Registriert: So 27. Nov 2022, 14:49
- Danke gegeben: 0
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 3 Beiträge
• Seite 1 von 1
• 3 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 5 Gäste