STATISTIK-FORUM.de

[timh86]

Hallo zusammen,
ich stehe bei der Interpretation eines Z-Score Diagramms etwas auf dem Schlauch.



Das Mean meiner unabhängigen Variable (X) liegt bei .746, die Std.Dev. bei .320, das Minimum bei 0, das Maximum bei 1.

Wenn ich es richtig verstanden habe, stellt bspw.
[*] der Z-Score = 0 exakt die Ergebnisse bei X = Mean (=.746) dar und
[*] ein Z-Score = 1 die Ergebnisse bei Mean + (1x) Std.Dev., also .746+.320=1.066.
[*] ein Z-Score = 2 die Ergebnisse bei Mean + (2x) Std.Dev., also .746+.640=1.386.

Nun frage ich mich, welche Bedeutung ein Z-Score von 1 oder gar 2 in diesem Diagramm haben kann, wenn X in diesem Beispiel doch niemals größer als 1 ist. Es kann doch gar kein X geben, welches bspw. 2 Standardabweichungen oberhalb des Mittelwerts liegt.

Kann mir jemand auf die Sprünge helfen?

Die Skalierung des Diagramms wurde vom Professor gewählt, aber mir ist es erst später aufgefallen.

[bele]

Hallo Tim,

zunächst einmal wäre es schön, ein wenig mehr über den Hintergrund zu erfahren. Worum es geht, was dieses Diagramm darstellen soll und persönlich bin ich ja ein Fan von beschrifteten Achsen. Aber ok, Du willst aus irgendeinem X aus dem Intervall [0, 1] ein Y vorhersagen und auf der y-Achse wird dieses Y abgetragen sein. Dann hast Du irgendeine Form von Regression gemacht und die "Fehlerbalken" markieren, wie sicher das Regressionsverfahren bei welchem x ist. Bei z = 0,5 sind die Fehlerbalken sehr klein, also liegen hier möglicherweise besonders viele Beobachtungen vor?

Insgesamt ist das Vorgehen etwas merkwürdig: z-Standardisierung ist oft sinnvoll, wenn der absolute Wert von x nicht so wichtig ist und vielleicht keine bedeutsame Erklärung hat. Wenn x aber in [0, 1] liegt ist der Verdacht naheliegend, dass der absolute Wert durchaus seine Berechtigung haben kann. Aber vielleicht handelt es sich um ein Regressionsverfahren, das aus anderen Gründen mit standardisierten Messwerte durchgeführt werden sollte? Entweder aus Konvergenzgründen oder weil man so hofft, den Einfluss verschiedener Prädiktoren vergleichbar zu machen?

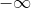
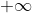
Bei sehr vielen statistischen Verfahren wird der Bequemlichkeit halber Normalverteilung angenommen. Dann kann man oft die Ergebnisse bis nach oder extrapolieren und irgendwelche parametrischen Annahmen machen, um wieviel ungenauer die Vorhersagekraft dann wäre. Wenn ich für eine Variable, die nur Werte von 0 bis 1 annehmen kann ein Modell verwende, dass sich dessen nicht bewusst ist, dann kann dieses Modell auch Vorhersagen treffen für Werte, die gar nicht beobachtet wurden. In Deinem Fall vielleicht auch für Werte, die gar a priori nicht beobachtbar sind. Da kann das Modell nichts für. Da muss man sich dann die Frage stellen, ob man bei diesem Modell bleiben möchte oder ob man ein passenderes Modell finden kann, ob man so ein Diagramm wirklich auch in den Bereichen zeichnen möchte oder ob man das Diagramm dann bei den z-Werte abschneidet, für die es noch eine Basis in den Daten gibt.

HTH,
Bernhard