Ein Kunde einer Bank will einen Kredit haben. Der Kredit soll 1 Mio. Euro betragen, über ein Jahr laufen und am Ende des Jahres getilgt werden. Die Bank stellt Nachfor- schungen über die Bonität des Kunden an und erfährt,
-> dass der Kunde mit einer Wahrscheinlichkeit von 70% Zinsen und Tilgung zahlt,
-> dass der Kunde mit einer Wahrscheinlichkeit von 20% weder Zinsen noch Tilgung zahlt,
->dass der Kunde mit einer Wahrscheinlichkeit von 10% zwar keine Zinsen zahlt, aber einen Betrag von X tilgt, wobei X eine stetige Zufallsvariable ist (in Mio. Euro) mit Dichtefunktion
-> fx(x)= 2x für 0<x<1
Welchen Zinssatz müsste die Bank fordern, damit sie eine erwartet Rendite von 6% erzielt.
Ich finde absolut keinen Ansatz für diese Problem und weiß nicht, wie ich das berechnen soll...
Data Science Klausuraufgabe
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
- lsd03
- Grünschnabel

- Beiträge: 6
- Registriert: Sa 11. Nov 2023, 11:02
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Data Science Klausuraufgabe
Sei 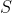 die Schuld des Kreditnehmers (also Kredit und 6% Zinsen) und
die Schuld des Kreditnehmers (also Kredit und 6% Zinsen) und 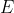 der Erwartungswert dafür, wieviel er zurückzahlt.
der Erwartungswert dafür, wieviel er zurückzahlt.
Dann sei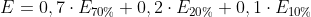
wobei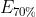 der Erwartungswert im 70%-Fall,
der Erwartungswert im 70%-Fall, 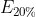 der Erwartungswert im 20%-Fall und
der Erwartungswert im 20%-Fall und 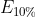 der Erwartungswert im 10%-Fall ist. Das sind bedingte Wahrscheinlichkeiten von einander ausschließenden Fällen: https://de.wikipedia.org/wiki/Bedingte_ ... inlichkeit
der Erwartungswert im 10%-Fall ist. Das sind bedingte Wahrscheinlichkeiten von einander ausschließenden Fällen: https://de.wikipedia.org/wiki/Bedingte_ ... inlichkeit
Ich kann Dir verraten, dass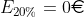 ist und dass Du auf
ist und dass Du auf 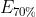 ganz leicht selbst kommen wirst.
ganz leicht selbst kommen wirst.
Bleibt also als Aufgabe noch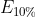 zu errechnen und da wir hier Hausaufgaben nicht lösen, sondern nur Hinweise geben, muss ich Dir den Teil selbst überlassen.
zu errechnen und da wir hier Hausaufgaben nicht lösen, sondern nur Hinweise geben, muss ich Dir den Teil selbst überlassen.
Viel Erfolg,
Bernhard
Dann sei
wobei
Ich kann Dir verraten, dass
Bleibt also als Aufgabe noch
Viel Erfolg,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Data Science Klausuraufgabe
Moin Bernhard, das ist auf jeden Fall ein super Hinweis!
Vielen Dank dir!
Vielen Dank dir!
- lsd03
- Grünschnabel

- Beiträge: 6
- Registriert: Sa 11. Nov 2023, 11:02
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Data Science Klausuraufgabe
Dann sei 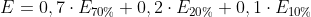
Ich kann Dir verraten, dass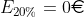 ist und dass Du auf
ist und dass Du auf 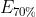 ganz leicht selbst kommen wirst.
ganz leicht selbst kommen wirst.
Bedeutet das dann, dass E= 0,7*1.060.000 + 0,2*0 + 0,1* (2/3*1.000.000)= 808.666,66
Oder wie kann ich das verstehen?
Weil E70% für mich die erwarte Rückzahlung des ganzen Betrags ist, und der Erwartungswert von E10% ist für mich ausgehend von der Dichtefunktion 2/3 also (2/3*1.000.000)
Das Ergebnis ergibt für mich aber noch nicht so richtig Sinn. Bitte nochmal um Hilfe.
Ich kann Dir verraten, dass
Bedeutet das dann, dass E= 0,7*1.060.000 + 0,2*0 + 0,1* (2/3*1.000.000)= 808.666,66
Oder wie kann ich das verstehen?
Weil E70% für mich die erwarte Rückzahlung des ganzen Betrags ist, und der Erwartungswert von E10% ist für mich ausgehend von der Dichtefunktion 2/3 also (2/3*1.000.000)
Das Ergebnis ergibt für mich aber noch nicht so richtig Sinn. Bitte nochmal um Hilfe.
- lsd03
- Grünschnabel

- Beiträge: 6
- Registriert: Sa 11. Nov 2023, 11:02
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Re: Data Science Klausuraufgabe
lsd03 hat geschrieben:Bedeutet das dann, dass E= 0,7*1.060.000 + 0,2*0 + 0,1* (2/3*1.000.000)= 808.666,66
Vielleicht ist das mein Fehler, ich hatte oben falsch geschrieben, dass die Schuld des Kreditnehmers der Kredit plus 6% sei. Das ist natürlich falsch. Die Schuld des Kreditgebers ist der Kredit plus der Zins, nach dem hier gefragt ist. Da hatte ich Dich wohl auf die falsche Spur gesetzt.
E10% ist für mich ausgehend von der Dichtefunktion 2/3 also (2/3*1.000.000)
"Ist für mich"?
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: Data Science Klausuraufgabe
Ist für mich, soll heißen, dass ich so gerechnet hatte^^
Aber wie gehe ich denn dann vor, unter der Annahme, dass ich falsch gerechnet habe?!
Aber wie gehe ich denn dann vor, unter der Annahme, dass ich falsch gerechnet habe?!
- lsd03
- Grünschnabel

- Beiträge: 6
- Registriert: Sa 11. Nov 2023, 11:02
- Danke gegeben: 1
- Danke bekommen: 0 mal in 0 Post
Thema bewerten: 




 • 6 Beiträge
• Seite 1 von 1
• 6 Beiträge
• Seite 1 von 1
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 3 Gäste


