Ich schreibe gerade an meiner Bachelorthesis und einen Teil davon bildet eine statistische Analyse einer Umfrage. Da ich im Rahmen meines Studiums keinerlei Kontakt zur Statistik hatte (Ich studiere Wirtschaftsrecht) bereitet dieser Teil mir ein wenig Sorgen. Darum war ich in der Bibliothek habe mir Bücher besorgt und auch bereits mehrere Tage im Internet verbracht aber ich bin noch nicht hunderprozentig davon überzeugt, ob das alles richtig ist was ich mache.
Zu meinem Fall:
In dieser Umfrage wird jährlich ein konzernweites Problem abgefragt. Die meisten Fragen sind mit Antwortvorgaben versehen, welche dann automatisch in Punkte umgerechnet werden. Anhand dieser Punkte ergibt sich dann das Gesamtergebnis in Prozent. Da ich überzeugt bin, dass nicht alle Fragen trennscharf sind, also manche Fragen den gleichen Indikator messen und somit aus Effizienzgründen (Die Umfrage wird nur durch CEOs beantwortet) vermieden werden könnten.
Dazu hab ich mir überlegt zunächst eine einfache Korrelationsanalyse zwischen den jeweiligen ausgewählten Fragen zu fahren und diese auf ihre SIgnifikanz im Rahmen eines T-Tests und dem P-Wert zu überprüfen. Besteht also eine signifikante Korreation zwischen zwei Fragen,messen diese den gleichen Indikator und eine Frage kann gestrichen werden. Weisen sie keinen Zusammenhang auf, sind beide Fragen berechtigt. Dies war auch kein Problem, ich habe einfach mit Excel den Korrelationskoeffizient R (=PEARSON) berechnet (Leider bin auf Excel angewiesen, da es auf der Arbeit kein SPSS/R gibt). Also konnte ich die Umfrage um nicht trennscharfen Fragen bereinigen.
Als nächstes hab ich mir überlegt, dass ich den in seinem Umfang nun verschlankten Fragebogen darauf untersuchen möchte, wieviel Einfluss bzw. welche Frage/Variable den größten Einfluss auf das Gesamtergebnis hat und bin dabei auf die Mehrfachregression gestoßen. Zur Mehrfachregression habe ich das Datenanalyse-Tool von Excel benutzt und habe nun Probleme anhand der Zahlen abzulesen, welche Frage den meisten Einfluss hat. Mein Betreuer stellt es sich so vor, dass ich quasi eine Rangreihenfolge nach Einfluss aufs Gesamtergebnis bilde. Soviel mal zur Theorie, ich hoffe ich bin bis hierhin nicht bereits auf dem Holzweg.
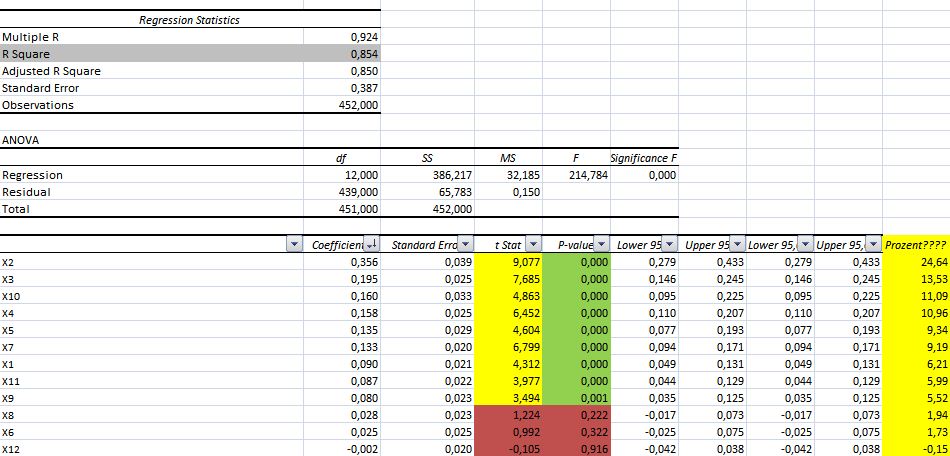
Ich habe dazu mal einen Screenshot eines Beispiels angehängt, vllt. kann mir ja jemand (Bitte mit so wenig Theorie und Formeln wie möglich) erklären, ob und woran ich dies ablesen kann, bzw. welche Werte wichtig für mich sind.
Laut meiner Recherche nimmt man dazu den T-Wert, welchen man mit einer T-Wert-Tabelle und seinem kritischen Punkt abgleicht. Ist dieser größer als der kritische Punkt, dann wird die Nullhypothese verworfen.
Alleine beim Abgleich mit der Tabelle hab ich schon Probleme, eine solche Tabelle hat ja die als eine Achse das Signifikanzniveau alpha (Bei mir 0,05) und die Freiheitsgrade (df). In meinem Beispiel hab ich für df jedoch 3 Auswahlmöglichkeiten:
-Regression 12,000
-Residual 439,000
-Total 451,000
Welchen Wert nehme ich für df? Ich habe mich für Residual entschieden und bekomme dann einen kritischen Wert von ca. 1,965 heraus, diesen vergleiche ich mit meinen berechneten T-Werten und dabei sind 9 von 12 größer als der kritische Wert. Ab jetzt verstehe ich gar nichts mehr
Das Thema Nullhypothese bereitet mir sowieso Verständnisprobleme, da ich zum korrelieren der Daten habe mir eine Liste an Hypothesen aufgeschrieben habe. Als einfaches, nicht umbedingt sinnvolles Beispiel könnte man z.B. zwei Umsatzzahlen aus verschiedenen Jahren korrelieren (Rein logisch müssen die alten Zahlen nicht abgefragt werden aber es ist ein anschauliches Beispiel). Eine Hypothese würde dann lauten "War der Umsatz eines Jahres hoch, ist auch der Umsatz des folgenden Jahres hoch". Eine Nullhypothese sagt ja aus, dass kein Unterschied zwischen zwei Werten besteht (Einfach ausgedrückt). Wäre diese formulierte Hypothese eine Nullhypothese?
Was bedeutet das verwerfen der Nullhypothese aufgrund des T-Werts bei der Regression? Ich wollte ja herausfinden, welche Variable den größten Einfluss auf das Endergebnis hat?
Wie ihr seht steh ich leider total auf dem Schlauch und ich hoffe jmd. erbarmt sich mir zu helfen, da ich mir es aus Büchern und dem Internet einfach nicht selbst erklären kann. Schonmal im Voraus ein dickes Dankeschön, falls sich jmd. die Zeit nimmt mir zu helfen.