STATISTIK-FORUM.de

[AmosOz]

Hallo liebe Forumsmitglieder,

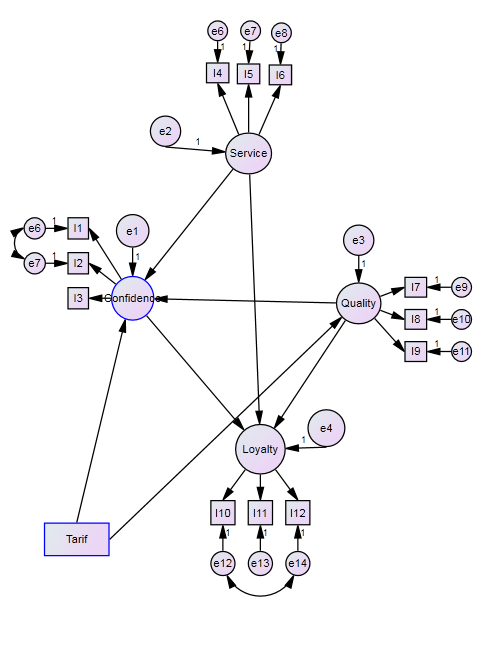
ich habe vor die Auswirkung 2 verschiedene Experimentalbedingungen auf nur zwei meiner Variablen zu messen. Kann ich dann die Experimentalbedinung als manifeste Variable (mit Intervall: 0;1) im SGM nehmen? (siehe Grafik)

Die manifeste Variable braucht auch keinen Fehlerterm, oder?

Wie sieht das mit der latenten exogenen Variable aus, brauche ich da den Fehlerterm?

Besten Danke und Grüße

AO

[Holgonaut]

Hi,

kannst du über die Studie etwas mehr erzählen?

Zu Deinen Fragen: Exogene Variablen haben nie Fehlerterme/varianzen. So auch deine manifesten exogenen nicht.

Und ja, du kannst sie als dummy mit reinnehmen.

Die Messfehler-Korrelationen der zwei Paare von Items weißen darauf hin, dass mit diesen Messmodellen was nicht stimmt. Schau dir noch
mal die items an und überlege noch mal, ob die wirklich alle 3 jeweils dasselbe messen.

Grüße
Holger

[AmosOz]

Hi Holger,

vielen Dank für Dein Feedback! Das ist bisher rein hypothetisch, noch ist nichts erhoben und soll später vielleicht irgendwann einmal dazu beitragen, wie sich verschiedene Tarife auf Kundenzufriedenheit und Kundenbindung auswirken. Im Moment steckt dieser Teil meiner Masterarbeit aber noch in den Kinderschuhen.

Die Messfehler-Korrelationen kommt daher, dass ich einfach ein anderes SGM eines Bekannten verwendet und entsprechend angepasst habe und vergessen habe, diese zu löschen. Dort war die Korrelation denke ich vertretbar, da sich diese Items inhaltlich besonders nahe waren.

Dann ist der Fehlerterm (e2) bei Service auch falsch, da es auch eine exogene Variable ist, oder?

PS: Hast Du vielleicht auch noch einen Literaturtipp für mich,auf den ich mich wegen der Dummy-Variable beziehen kann, warum ich das so und nicht als Multi-Gruppen-Analyse mache?

Merci!

Viele Grüße

AO

[Holgonaut]

Hi,

Die Messfehler-Korrelationen kommt daher, dass ich einfach ein anderes SGM eines Bekannten verwendet und entsprechend angepasst habe und vergessen habe, diese zu löschen. Dort war die Korrelation denke ich vertretbar, da sich diese Items inhaltlich besonders nahe waren.

Items sollten sich "nahe" sein, weil sie den selben Faktor messen. Eine Fehlerkorrelation bedeutet, dass der gemeinsame Faktor die Kovarianz der items nich vollständig erklären kann. Das kann
trivial sein (d.h. alle 3 items messen tatsächlich den existierenden Faktor - nur haben sie einen Begriff gemeinsam); es kann aber auch fundamental sein - d.h. das gesamte Ein-Faktor-Modell ist falsch
und stattdessen wäre ein 2-Faktormodell angemessener (was impliziert, dass der modellierte Faktor nicht existiert).

Und ja, der service-Fehlerterm ist Käse.

Wegen der dummy-Variable siehe:

Russel, D. W., Kahn, J. H., & Altmaier, E. M. (1998). Analyzing data from experimental studies: A latent variable structural equation modeling approach. Journal of Counseling Psychology, 1, 18-29.

Grüße
Holger