Hallo Sghrn,
erstmal entspann Dich mal

Ich hab dir fehlendes Hintergrundwissen unterstellt, nicht dir "alle Fähigkeiten abgesprochen". Das war außerdem als Anregung und Kritik gemeint, nicht Angriff auf Deine Person. Daher kein Grund, so dünnhäutig zu reagieren. Ich kenn Dich und Deine Erfahrung natürlich nicht und kann nur das beurteilen, was du hier tust (Deine Modellspezifikation) und schreibst (v.a. der Satz mit der Haarspalterei). Du hast also das nötige Wissen, ok. Dann erscheint es aber halt seltsam, wie du Dein Modell so spezifizierst und so fundamentale Dinge wie die kausale Spezifikation (und darum geht es bei dem Unterschied zwischen reflektiv und formativ) als Haarspalterei bezeichnest. Und das hab ich (nach wie vor zurecht kritisiert).
Ich befürchte auch du hast meine Antwort zu Punkt e nicht verstanden. Woraus leitest du Dogmatismus hab? Es geht in einem Modell allgemein und bei Messmodellen im Spezifischen darum, dass du DEIN Verständnis von der Welt bzgl. der Variablen und ihrer kausalen Verknüpfung modellierst. Ich wäre jetzt versucht, mich zu wiederholen, deshalb kopier ich den zentralen Satz aus meiner Antwort einfach:
"Stellst du dir deine AV nämlich als eine unbeobachtete singuläres Merkmal vor, dass existiert und Effekte auf andere Variablen hat (u.a. die Masse von Indikatoren) bedeutet das was völlig anders als wenn du sie als Summe all dieser Indikatoren interpretierst. Im ersten Fall machst du implizit die Aussage, dass sie überhaupt existiert - während dies im zweiten Fall nicht der Fall ist (weil DU als Schöpfer sie durch die Summierung quasi ins Leben rufst...."
Und da war einfach ein Widerspruch: Wenn du "Ausmaß" als Summenindex *konzeptualisierst*, aber im Modell als reflektive Variable *spezifizierst*, ist das Modell einfach fundamental falsch. Die darin spezifizierte latente Ausmaß-Variable existiert überhaupt nicht (weil die Indikatoren keinen einzelnen zentralen common cause haben, der sie alle beeinflusst), oder sie existiert zwar, hat aber eine völlig andere Bedeutung. Und damit sind auch alle Effekte der Prädiktoren Murks. Und wenn du dann schreibst, dass du dich in den Folgen von Misspezifikationen auskennst, kann ich nicht kapieren, dass du das als Haarspalterei bezeichnest.
Und nochmal: Ich gebe keinen Weg vor (deshalb kein Dogmatismus), sondern sage nur, dass sich Leute Gedanken machen müssen, wie ihre Vorstellung von der Welt ist und diese exakt umsetzen und testen. Im übrigen machen das auch die Experten falsch. Ich war die letzten beiden Tage auf einer internationalen SEM-Tagung, da hört man schon einiges, was in die selbe problematische Richtung geht.
Wenn du jetzt einen Index aus allen Indikatoren bildest, ist das schon besser. Ich mach das im Zweifel auch so. Es gibt dabei nur eine Gefahr: Wenn du eine UV hast, die einen Effekt auf einen Index hat, dann ist ihr geschätzter Effekt der Mittelwert aller Beziehungen mit allen einzelnen Indikatoren. Das kann übel sein, wenn manche der Beziehungen niedrig oder null sind. Ich würd mir also die einzelnen Beziehungen mal angucken.
Dein quote von Albers und Hildebrandt bezieht sich glaub ich auf die Zusammenfassung von Prädiktoren in Regressionsmodellen, die ich hochproblematisch finde. Dies basiert auf dem fehlen einer realistischen Wissenschaftsorientierung (in der es darum geht, die kauslen Effekte von existierenden Phänomenen zu untersuchen), sondern wird häufig im Rahmen einer reinen auf Prädiktion ausgelegten Auffassung der Regressionsanalyse empfohlen. Aber: Wenn zwei Variablen (die auch wirklich zwei verschiedene Dinge sind) hoch korrelieren, bekommst du bei getrennter Modellierung dennoch unverzerrte Effekte (einzig die Standardfehler werden erhöht). Wenn du sie zusammenaddierst, bekommst du einen Mischmasch der Effekte.
Zur Quote von Hulland (meinst du Holland?): Es sind nicht die Indikatoren, die reflektiv oder formativ sind! Es ist die Struktur der Beziehungen. Ein Item wie "ich bin ordentlich bei der Arbeit" kann gleichzeitig eine reflektive Messung des traits Gewissenhaftigkeit sein oder ein formatives von job performance. Wieder: Es geht darum, sich zu fragen, um was für ein Konstrukt es sich handelt und wie
die Beziehung der Indikatoren zu DIESEM Konstrukt ist.
In diesem Zusammenhang war der Artikel von Wilcox et al. für mich echt ein eye-opener.
Wilcox, J. B., Howell, R. D., & Breivik, E. (2008). Questions about formative measurement. Journal of Business Research, 61, 1219-1228.
In der Literatur wurde über formative Konstrukte so viel Komisches Zeug geschrieben (allem voran von Diamantopolous), dass es sehr viel Verwirrung hierzug gibt. Es gibt auch noch einen schönen Artikel von Howell, Breivik und Wilcox, in dem sie das kritisieren:
Howell, R. D., Breivik, E., & Wilcox, J. B. (2007). Reconsidering formative measurement. Psychological Methods, 12(2), 205-218.
In meinem Modell bleibt auf kausaler/logischer Ebene z.B. unklar, ob z.B. die "Erwartung des Bedankens" durch den Wunsch nach Anerkennung ausgelöst wird, oder ob ob das Erfahren des Danks selbst die Anerkennung ist. Letztlich könnte aber doch beides erklären, wie Internetpiraterie zustande kommt.
In Querschnittsmodellen ist Kausalität meist unklar - dahingehend, dass es immer die Möglichkeiten für alternative Strukturen geben kann: Modelliere DEIN Verständnis und schau, ob es Evidenz dagegen gibt (misfit). Mehr kann man nicht tun.
In meinem Modell bleibt auf kausaler/logischer Ebene z.B. unklar, ob z.B. die "Erwartung des Bedankens" durch den Wunsch nach Anerkennung ausgelöst wird, oder ob ob das Erfahren des Danks selbst die Anerkennung ist. Letztlich könnte aber doch beides erklären, wie Internetpiraterie zustande kommt.
Hier kommen wir zu einem Kern der Konfussion. Wenn du das Konstrukt als *Summe der Teile" konzeptualisierst, dann existiiert dieses Konstrukt außerhalb dieser Bestimmung nicht, denn DU hast es durch die Definition, welche Teile dazu gehören ins Leben gerufen. Wenn du das Konstrukt modellierst, wie es Jahrzehnte in der Literatur gemacht wurde (mit den Indikatoren, die einen Effekt auf eine latente Variable haben und diese hat auch wieder Effekte auf andere outcomes), dann ist es kein formatives Konstrukt, sondern ein ganz gewöhnliches Kausalmodell mit Präditkroen (den "Indikatoren"), einem Mediator (der latenten Variablen) und AVs. Die latente Variable existiert hierbei und könnte auch durch reflektive Indikatoren gemessen werden (siehe Vorschlag von Howell et al.)
In der Literatur werden beide zusammen geworfen (v.a. von den Marketing-Leuten wie Diamantopoulus). D.h. man konzeptualisiert das Konstrukt als in Index (Summe der Teile), aber modelliert es als Kausalmodell.
Zu dem SEM von Dördrechter. Ich kann das natürlich nicht beurteilen. Es kommt wie gesagt auf die Formulierung der items an. Vielleicht hat er ja homogene und kongenerische (reflektive) Messungen von Ausmaß entwickelt? Denk an mein o.g. Beispiel zu job performance: Du könntest formative Items (ich vermeide hier den Begriff Indikator, weil er m.E. falsch ist) entwickeln, die sich auf Determinanten einer allgemeinen Einschätzung der eigenen performance beziehen (ich bin pünktlich, mache gute Produkte, halte deadlines etc.) und du könntest 3 reflektive entwickeln (ich leiste insgeamt gute Arbeit etc.) Letzteres könnte man als reflektives Modell modellieren, ersteres als formatives (oder am besten beide zusammen).
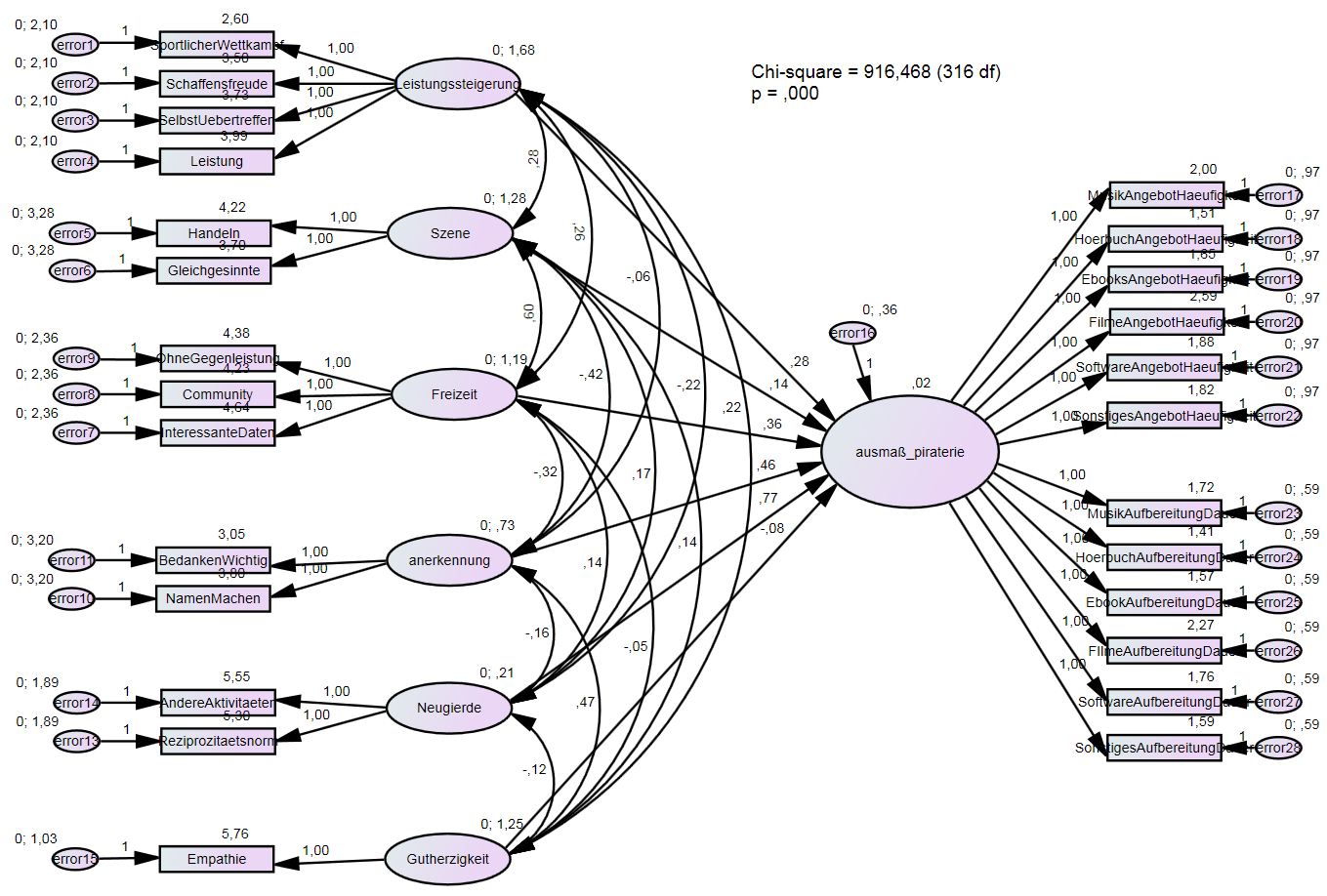
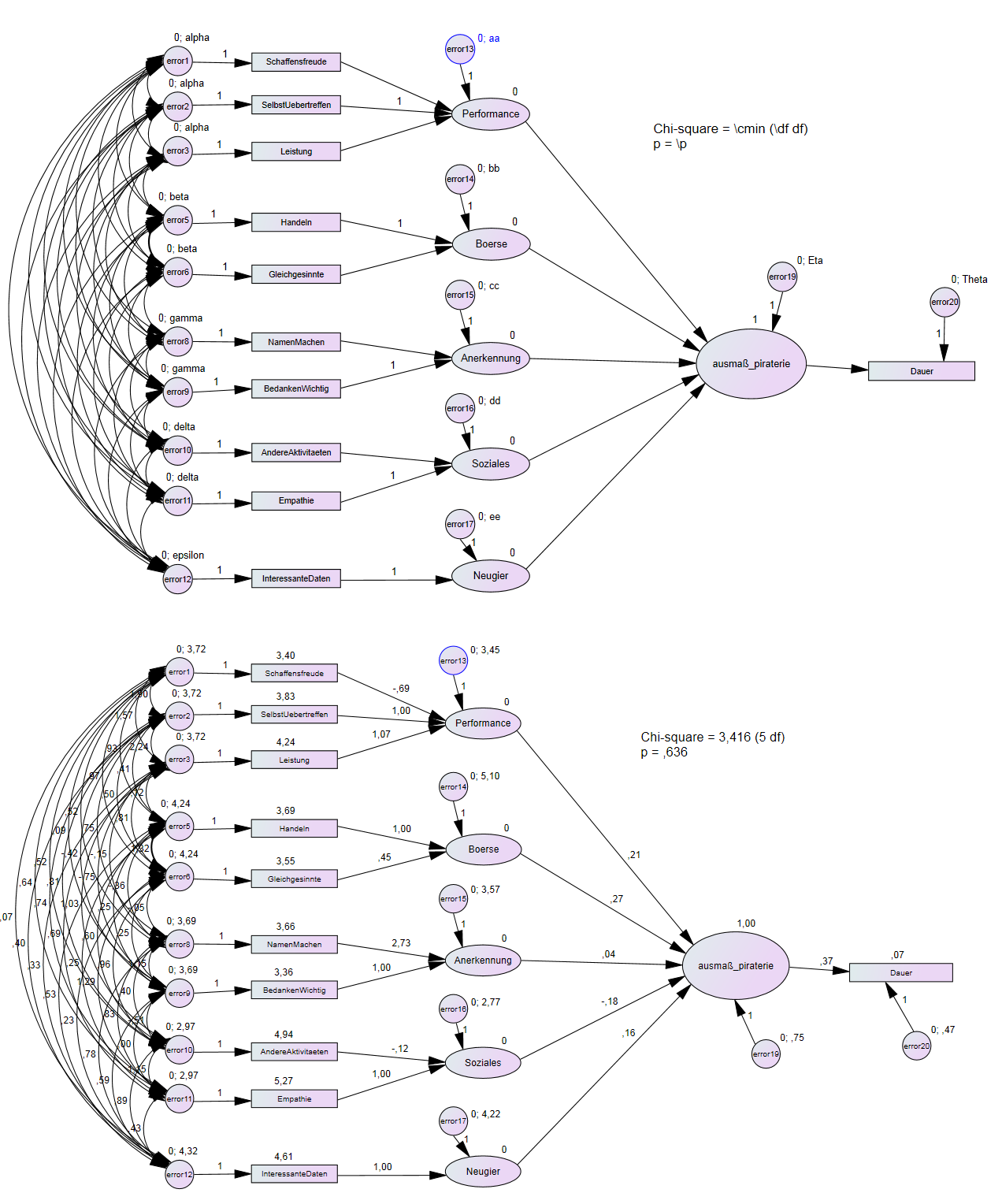
Abgesehen davon ist das Modell von Dördrechter seltsam: In dieser Form wäre es nicht identifiziert, weil die latente Variable im formativen part nur ein outcome hat (sie braucht mindestens 2)...
Ich hoffe, ich bin dir nicht wieder durch irgendwas zu Nahe getreten. Mein Ziel ist es, Deine teilweisen problematischen Auffassungen zu korrigieren und Dein Modell richtig zu spezifizieren. Und Deine Auffassungen sind eben v.a. auch dadurch problematisch, weil du sie aus der Literatur hast, die - wie oben beschrieben - selbst sehr unklar ist (um mal den Begriff Unfug zu vermeiden).
Ich hab das alles in Windeseile runtergeschrieben und hoffe, es war verständlich genug. Wenn nicht, klären wir das

Grüße
Holger