Holger,
ich kann das gerne in verkürzter Form weiter ausführen, möchte aber für eine ausführliche Erklärung auf die angegebene Literatur verweisen.
Betrachten wir zunächst den linearen Fall. Es sei
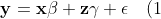)
das "wahre" Modell. Wird stattdessen das Modell
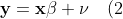)
unter Vernachlässigung von

geschätzt, dann gilt für den geschätzen Koeffizienten
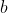
(unter Vernachlässigung der eigentlich nötigen Erwartungswertschreibweise)
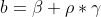
wobei
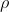
die Korrelation von
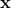
und

widerspiegelt. Ist diese Korrelation
und der Koeffizient
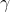
von Null verschieden, ist die Schätzung für
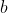
offensichtlich verzerrt (Greene, 2008: 134).
Da in (1) und (2)
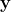
beobachtet ist, können wir die Residualvarianz

bzw.
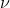
aus den Daten schätzen (wir kennen das Ergebnis als Residuenquadratsumme).
Nun betrachten wir nicht-lineare Modelle (wie Logit-Modelle). Dabei sei
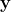
in (1) und (2) eine latente Variable. Wir beobachten in den Daten die Ausprägung Null, falls
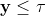
und den Wert Eins, falls
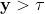
(zur Herleitung des Logit-Modells über eine latente Variable vgl. Long, 1997: 40ff).
Da
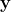
nicht beobachtet ist, können wir die Residualvarianz

bzw.
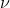
in diesem Fall nicht mehr aus den Daten schätzen. Zur Identifikation des Modells müssen daher zwei Annahmen gemacht werden. Erstens nehmen wir für
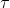
den Wert Null an (auch andere Werte sind möglich, das ist hier irrelevant). Die zweite Annahme betrifft

bzw.
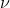
. Hier nehmen wir eine bestimmte Vereilung für die Fehlterme an. Nehmen wir eine standard-logistische Verteilung an, führt das zum Logit-Modell, die Annahme einer standard-Normalverteilung resultiert im Probit Modell (für die Herleitung in wenigen Zeilen vgl. Long, 1997).
Bleiben wir beim Logit-Modell, das in diesem Thread benutzt wurde. Durch die Verteilungsannahme fixieren wir die Residualvarianz auf
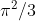
. Das hat Konsequenzen. Wir unterstellen nämlich damit, dass
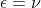
gilt. Wenn

mit
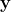
korreliert, wenn also
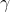
von Null verschieden ist, dann ist diese Unterstellung falsch. Die "wahre" Residualvarianz in (1) ist dann nämlich kleiner als in (2). Da wir die Residualvarianz aber per Annahme fixieren folgt daraus, dass die Varianz von
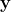
in (1) größer sein muss als in (2). Das ist deshalb so, weil sich die Varianz in
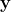
aus einem erklärten und einem unerklärten (residualen) Teil zusammensetzt. Wenn der erklärte Teil größer wird, was der Fall ist, wenn
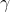
von Null verschieden ist, dann muss bei fixierter Residualvarianz die Gesamtvarianz steigen.
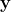
hat in (1) demnach eine andere Metrik als in (2).
Um diesen Umstand in die Modelle zu integrieren schreiben wir die Fehlterme um und bekommen
)
und
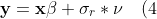)
wobei
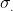
einen Skalierungsfaktor darstellt, der die "wahre" Residualvarianz zu der per Annahme unterstellten ins Verhältnis setzt. In (3) und (4) gilt daher
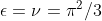
. Aus diesen Überlegungen folgt, dass wir für
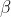
in (3) und (4)
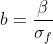
bzw.
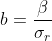
schätzen (Karlson und Holm, 2011; Mood, 2010). Wenn (3) das wahre Modell ist, dann ist die Schätzung von
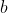
in (4) offensichlich verzerrt. Sie wäre nur dann unverzerrt, wenn
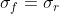
gilt, was wie gezeigt nur dann der Fall ist, wenn
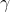
nicht von Null verschieden ist.
Dieses Ergebnis gilt unabhängig von der Korrelation von
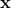
mit

, die wir hier nicht betrachtet haben. Eine mögliche Korrelation spielt natürlich eine zusätzliche Rolle für die Verzerrung, aber dafür möchte ich dann (erneut) auf den exzellenten Aufsatz von Carina Mood (2010) verweisen.
Literatur
Greene,William H. (2008). Econometric Analyses. Pearson.
Long, Scott (Hg.) (1997). Regression Models for Categorical and Limited DependentVariables. Thousand Oaks: Sage Publications.
Karlson, Kristian Bernt und Holm, Anders (2011). Decomposing primary and secondary effects: A new decomposition method. Research in Social Stratification and Mobility, 29(2):221–237.
Mood, Carina (2010). Logistic Regression: Why We Cannot Do What We Think We Can Do, and What We Can Do About It. European Sociological Review, 26(1):67–82.
Ebenfalls
Karlson, Kristian Bernt; Holm, Anders und Breen, Richard (2010). Comparing regression coefficients between models using logit and probit: A new method. URL
http://www.yale.edu/ciqle/Breen_Scaling%20effects.pdfStata is an invented word, not an acronym, and should not appear with all letters capitalized: please write “Stata”, not “STATA”.





