STATISTIK-FORUM.de

[jareeth]

Da in meiner aktuellen Regressionsgleichung die Annahme der Linearität verletzt ist, habe ich eine Transformation einiger Variablen vorgenommen um dies zu ändern.
Nun zu meiner Frage:
Ist es erlaubt jede mögliche Transformation vor zunehmen? Wieso beeinflusst das nicht das Modell, da ja nach der Transformation die Daten der Variable stark verändert sein können?
Der Datenbereich der Variable x auf die sich meine Frage bezieht ist [0,1]. Die von mir vorgeschlagene Transformation ist von x auf 1/((x^2)+0.1)). Das 0.1 noch in den Nenner addiert wird, hat als Begründung, dass die Transformation auch für die Datenpunkte möglich ist, die 0 als Wert haben.
Mit dieser Transformation ist keine Annahme der klassichen linearen Regression mehr verletzt, allerdings stellt sich mir die Frage ob die Transformation die Daten nicht verfälscht?
Bsp:
Ist ein Datenpunkt xi = 0.5 ist dieser nach der Transformation gleich 2,86. Wenn ein Datenpunkt xj allerdings den Wert 0 hat, ist dieser nach der Transformation gleich 10. Hier stimmt also die Relation innerhalb der Daten nicht mehr.

Ist diese Transformation dennoch zulässig?
Sollte ich die Transformation lieber nur auf die Datenpunkte anwenden, die ungleich 0 sind, und die restlichen einfach gleich 0 lassen?

Danke für eure Hilfe, ich bin gerade wegen dieser Frage einfach geblockt an meiner Bachelorarbeit weiterzuarbeiten...

[bele]

Das ist eine krasse Transformation, aber es ist eine monotone Transformation: wenn x größer wird, wird das transformierte x kleiner. Wenn Du beweist, dass ein Prädiktor das transformierte x kleiner macht hast Du auch bewiesen, dass es x größer macht. Genau bis dahin ist die Transformation nützlich, aber Du hast völlig Recht: alles andere ist völlig verdreht. Sätze wie "Ein Anstieg des Prädiktors um eins geht einher mit einem Anstieg von x um..." sind damit sicher nicht möglich. Ob das für Dich und Deine Frage passt musst Du schauen.

Vielleicht führt auch eine nichtlineare Regression (GAM?) zu einem guten Ergebnis mit weniger Knoten im Kopf?

HTH, Bernhard

[jareeth]

Danke für deine schnelle Antwort Bernhard!
Ich fokussiere mich sowieso auf die Interpretation einer anderen Variable, also denkst du ich sollte die Transformation verwenden? Diese transformierte Variable ist am Ende sowieso insignifikant und die Interpretation deshalb zu vernachlässigen.

LG Jareeth

[PonderStibbons]

Da in meiner aktuellen Regressionsgleichung die Annahme der Linearität verletzt ist

Wie wurde das festgestellt? Und wie äußert sich das, welche Form hat die Beziehung?

Ist es erlaubt jede mögliche Transformation vor zunehmen?

Was mathematisch möglich sein mag, ergibt inhaltlich meist keinen Sinn. Wie soll man denn die transformierten
Variablen und deren Beziehungen noch sinnvoll interpretieren?

Was sind das eigentlich für Variablen und wie groß ist die Stichprobe?

Mit freundlichen Grüßen

PonderStibbons

[jareeth]

Ich habe die partiellen Residuen gegen die Kovariablen abgetragen und es sind klare Unterschiede in beiden Funktionen zu sehen (vor allem in der "team" Variable).
Die Graphik mit den partiellen Resiuden: https://1drv.ms/u/s!AkIj1ZNxZc9AgcR8NHQ ... w?e=dUhn0A

Die Stichprobe ist leider mit n = 21 sehr klein, ich habe aber leider nicht mehr Daten finden können und muss jetzt mit den wenigen arbeiten. Einerseits beschreiben die Variablen finanzielle Kennzahlen, andererseits Kompetenzen pro Angestellten in der jeweiligen Kategorie.

LG Jareeth

[jareeth]

Wenn ich nur die eine Variable, die nicht transformiert wird, interpretieren müsste, ist es dann egal wie ich die andere Variable transoformiere? Oder beeinflusst die transformation alle anderen Variablen auch?

[PonderStibbons]

Ich sehe da eigentlich keine Veranlassung, mit Transformationen massiv an den Daten herumzuschrauben.
Mit n=21 lässt sich über Linearität praktisch nichts sagen, auch nach einer Transformation. Vieles kann an
einem bis zwei markant von anderen abweichenden Werten liegen.
Gibt es überhaupt irgendeine theoretische Basis für die Transformationen? Eine Aussage "der
Zusammenhang zwischen den 1/((x^2)+0.1))-transformierten Schulden und der abhängigen Variable
ist b=0,8" wäre vielleicht etwas zu fern liegend. Logarithmieren von UV und AV kann hingegen
oft auch inhaltlich sinnvoll sein, wenn es z.B. um Geld und Güter geht.

Mit dieser Transformation ist keine Annahme der klassischen linearen Regression mehr verletzt,

Das ist mit n=21 eigentlich nicht zu belegen.

Soll es ein Modell werden mit k=9 Prädiktoren bei n=21 Beobachtungen?

Mit freundlichen Grüßen

PonderStibbons

[bele]

Hallo!

Das ist eine schwierige Kiste.

Soll es ein Modell werden mit k=9 Prädiktoren bei n=21 Beobachtungen?

Das macht alles schwierig und eigentlich ist man an der Stelle versucht, es einfach sein zu lassen. Gehen wir mal davon aus, dass das keine Option ist und David gegen Goliath kämpfen muss. So ein Modell hat eigentlich nur eine Chance, wenn die Messfehler klein und die Modellspezifikation korrekt sind. Wenn man glauben würde, dass die korrekte Modellspezifikation ist, und wenn es nicht um die Interpretation von 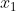geht, sondern das eine echte Kovariate ist, die nur helfen soll, ein 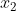besser auszuwerten, dann sollte man das unbedingt tun, dann sollte man diese Transformation vornehmen.

Richtig ist aber auch, dass 21 Beobachtungen zu wenig sind um einem zu sagen, was die korrekte Modellspezifikation ist und welche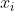 gebraucht werden. Dazu kommt noch dieser etwas beliebig wirkende Wert von 0,1 im Nenner. Warum nicht 1 oder 0,001? Das hat ja enorme Auswirkungen, wenn wird, und wenn das nicht passierte, bräuchte man den Term gar nicht.

Auch die Aussage, dass der zu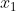 gehörende Koeffizient 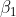sowieso nicht signifikant wird bringt keine Hilfe, da man bei 9 Prädiktoren für 21 Beobachtungen grundsätzlich Nicht-Signifikanz als Normalfall und Signifikanz als sehr bemerkenswertes Ereignis sehen muss.

Ich glaube nicht, dass es eine einfache, korrekte Antwort auf die Frage gibt. Ich sehe zwei mögliche Herangehensweisen:

1. puristisch, wahrscheinlich das, was PonderStibbons im Sinn hat: Wenn es keine theoretische Grundlage für eine Transformation gibt und bei mangelnden Daten keine empirische Grundlage für eine Transformation gibt, dann lass die Transformation weg, rechne ein Standardmodell und komme zu dem Ergebnis, dass nichts signifikant wird. Dann beschreib, dass nichts signifikant geworden ist und erkläre es mit der dünnen Datenlage. Wenn doch etwas signifikant würde steckst Du in Schwierigkeiten, weil Du dann wahrscheinlich eine Effekststärke unterstellen musst, die Dir keiner glaubt.

2. die Datenquetsche: Wenn es auf der Welt nur 21 Datensätze gibt, dann kann man trotzdem versuchen, möglichst viel da herauszuholen. Ich glaube, dazu würde ich die Transformation durchführen und hier tatsächlich auf Bayes-Statistik umsteigen. Das hat zwei Gründe: Erstens ließe sich vielleicht für den einen oder anderen Prädiktor ein tatsächlich informativer Prior beschreiben, was dem ungünstigen -Verhältnis helfen würde. Außerdem könnten gut gewählte Prior-Verteilungen das ganze etwas regularisieren, dass nicht einzelne Daten einzelne Koeffizienten in die Höhe treiben. Zweitens kann man in einer Bayes-Regression beschreiben, wie sich meine Erwartungen an die Bedeutung einzelner Prädiktoren aufgrund der Daten verändert, auch wenn nichts signifikant wird. Man könnte beispielsweise sagen: "Vor der Regression war unsere Erwartung, dass der Koeffizient von 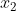positiv ist bei 50%, aufgrund der Daten ist sie auf 85% angestiegen." Sind 85% ein Beweis? Nein. Habe ich damit quantifiziert, was sich in den wenigen, 9-dimensionalen Beobachtungen versteckt? Ja. Die oben verlinkte Grafik könnte zu R passen. In R lässt sich eine lineare Regression als Bayes-Regression mit dem Paket rstanarm und darin der Funktion stan_glm() leicht rechnen - sieht fast so aus wie eine klassische lineare Regression mit lm(). Das ändert natürlich nichts daran, dass man gute Prior-Annahmen formulieren und begründen muss, was sicher nicht banal wird.

JMTC,
Bernhard

[jareeth]

Hallo,
zuerst möchte ich Danke sagen für eure Bemühungen mir weiterzuhelfen!

Ja tatsächlich sind es k = 9 und n = 21

Ihr seid der Meinung, dass durch die geringe Datenmenge in keinem Fall etwas signifikantes resultieren kann, selbst wenn die Tests eine Signifikanz liefern?
Hier ist eine Abbildung der summary(model) meines (nicht transormierten) Modells zu sehen: https://1drv.ms/u/s!AkIj1ZNxZc9AgcUfZN3 ... A?e=MnITJx

Ich habe eben das Problem, dass ich nur den kleinen Datensatz habe und in meiner Arbeit vorankommen muss... Deswegen hätte ich versucht, wenn alle Annahmen erfüllt sind, eine Interpretation des Modells vorzunehmen, und basierend darauf meine Diskussion zu führen. Anschließend natürlich im Limitationsteil auf die geringe Datenmenge und die Interpretationsproblematik einzugehen.

[bele]

Hallo,

ich muss zugeben, ich bin verblüfft und hätte damit nicht gerechnet. Ich habe nicht gesagt, dass da nichts resultieren kann, aber ich habe auch nicht damit gerechnet. So Daten will ich auch mal haben.

Glückwunsch!
Bernhard