PonderStibbons hat geschrieben:Die Variable kannst Du entweder als kategorial auffassen oder
als ordinal. Sind das immer dieselben Leute, oder jahresweise
unterschiedliche Befragte? In letzterem Fall rechnest Du einen
Chi²Test (kategoriale Auffassung), oder einen Mann-Whitney
U-Test (ordinale Auffassung). Falls mehr als 2 Jahre gleichzeitig
betrachtet werden sollen, dann einen Kruskal-Wallis H-Test statt
dem U-Test.
Mit freundlichen Grüßen
P.
1. Es sind jahresweise unterschiedliche Befragte. (Das heisst es könnte theoretisch durch Zufall dazu kommen, dass eine Person zweimal gefragt wird in unterschiedlichen Jahren) denke aber trotzdem dass es als unabhängige Verteilungen zählt.
Stimmt diese Überlegung?
Was ist dann die Aussage wenn ich einen Chi^2 Test mache und was ist die Aussage eines U-Test? respektive: Was untersuche ich dann genau?
Ich habe mir überlegt, dass eben z.B: ein T-Test gar keinen Sinn machen würde, da es ja nicht ein durchschnitt von Prozentzahlen sind sondern einfach eine Prozentzahl. Es gibt ja keine Varianz in den Anteilen sondern es wird einfach jedes Jahr geschaut welcher Anteil sich wo einträgt und dann ist das die Prozentzahl... Deshalb kann man keinen T-Test machen.
(In einer anderen Frage: Wie viel Prozent ihres Vermögen haben Sie in Aktien angelegt? ist es ja schon anders oder? Da habe ich dann eine durchschnittliche Prozentzahl mit einer gewissen Varianz und kann untersuchen ob die Nullhypothese (Die Anteile sind gleich) zu verwerfen ist.
Ich habe jetzt beide Tests einmal durchgeführt.
Einmal habe ich die Variable als Nominal gelassen so wie es war und habe den Chi Quadrat Test gemacht.
(Dabei habe ich in der Zeile das Jahr und in der Spalte die Risikoneigung. Ist das richtig so? oder muss ich das umgekehrt machen?)
Dabei habe ich einen Chiquadratwert von 9.73 erhalten bei 2 Freiheitsgraden --> Asymptotische Signifikanz: 0.08. Heisst das, dass ich die Nullhypothese (dass es keinen unterschied zwischen den beiden Jahren gibt) verwerfen kann? Dieser Test ist ja zweiseitig. Wenn ich aber iwie zeigen möchte, dass die Leute vorallem vermehrt risikoabgeneigt wurden müsste ich doch einen einseitigen Test machen... Geht das?
(EDIT: Oder wird das mit einem U-Test gemacht? Da gibt es ja einen sogenannten mittleren Rang. Heisst das wenn der Rang tief ist, dass dann vermehrt die die Tendenz Risikoabgeneigt gewählt wurde, da dies ja ein kleinerer wert ist (1 anstatt Risikofreudig 3)?)
Für den U-Test habe ich die Variable geändert in Ordinal.
Als Testvariable habe ich die Risikobereitschaft gewählt (1,2 oder 3)
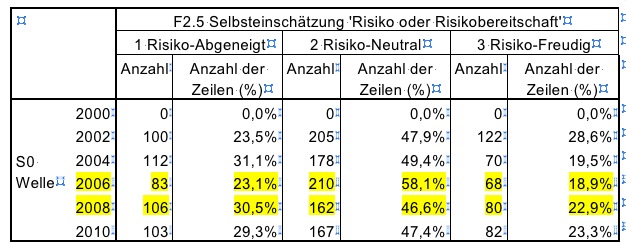
und als Gruppenvariable habe ich das Jahr genommen (2006 und 2008)
Das hat mir eine Asymptotische Signifikanz gegeben von .35. Weshalb ist dieser Wert so viel höher? Sollten nicht beide etwa gleich sein?
Was kann ich daraus schliessen?
Noch eine andere Frage: muss es für diese Tests nicht sein, dass die Variablen normalverteilt sind? (Geht das überhaupt wenn ich nur 3 Kategorien habe?)
Vielleicht kann mir jemand zu diesen vielen Fragen ein paar Antworten geben.
Besten Dank
Gruss radiohead3