Hallo Community,
ich habe 64 Versuche mit drei vierstufigen Faktoren. Der Versuchsplan ist vollfaktoriell, jeder Versuch wurde also nur einmal ausgeführt. Ich habe versucht die Auswertung mit der anovan-Funktion von Matlab durchzuführen, die Prüfgrößen sind dabei alle unendlich. Liegt das daran, dass jeder Versuch nur einmal ausgeführt wurde? Wie kann ich die Signifikanzen der Faktoren trotzdem bestimmen?
Vielen Dank im Voraus für die Antworten!
4^3 vollfaktoriellen Versuchsplan auswerten
- MechIng123
- Grünschnabel

- Beiträge: 6
- Registriert: Mo 18. Mai 2020, 11:51
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Wenn in jeder Zelle des Versuchsplanes n=1 Beobachtung ist, dann hast Du keine Freiheitsgrade und Inferenzstatistik ist weder sinnvoll noch möglich.
Mit freundlichen Grüßen
PonderStibbons
Mit freundlichen Grüßen
PonderStibbons
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11372
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Hi,
danke für die Antwort! Der Haken an der Sache ist, dass es sich um Strömungssimulationen handelt. Wenn ich einen Versuch mit den selben Einstellungen wiederholen würde, würde ich die selben Ergebnisse erhalten. Kann ich trotzdem irgendwie herausbekommen, was für einen Einfluss meine Parameter auf die Zielgrößen haben?
danke für die Antwort! Der Haken an der Sache ist, dass es sich um Strömungssimulationen handelt. Wenn ich einen Versuch mit den selben Einstellungen wiederholen würde, würde ich die selben Ergebnisse erhalten. Kann ich trotzdem irgendwie herausbekommen, was für einen Einfluss meine Parameter auf die Zielgrößen haben?
- MechIng123
- Grünschnabel

- Beiträge: 6
- Registriert: Mo 18. Mai 2020, 11:51
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Kann ich trotzdem irgendwie herausbekommen, was für einen Einfluss meine Parameter auf die Zielgrößen haben?
Was genau meinst Du damit? Die Varianzzerlegung hast Du doch bereits.
Du kannst auch ein Modell rechnen lassen, in dem nur die Haupteffekte
vorhanden sind, ohne die Interaktionen.
Mit freundlichen Grüßen
PonderStibbons
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11372
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Meinst Du ein Regressionsmodell? Kann ich dann anovan darauf anwenden, um die Haupteffekte zu bekommen, oder funktioniert das anders?
- MechIng123
- Grünschnabel

- Beiträge: 6
- Registriert: Mo 18. Mai 2020, 11:51
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Normalerweise erlaubt es eine Statistiksoftware dem Anwender zu bestimmen,
ob Interaktionen bei einer Varianzanalyse eingeschlossen werden oder nicht.
ob Interaktionen bei einer Varianzanalyse eingeschlossen werden oder nicht.
- PonderStibbons
- Foren-Unterstützer

- Beiträge: 11372
- Registriert: Sa 4. Jun 2011, 15:04
- Wohnort: Ruhrgebiet
- Danke gegeben: 51
- Danke bekommen: 2504 mal in 2488 Posts
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Dann ist Matlab wahrscheinlich nicht das richtige Tool. Wie würde ich das denn in R machen? Ein Regressionsmodell mit meinen Daten erstellen und anova darauf anwenden? Aber wie stelle ich da ein, dass Interaktionen nicht eingeschlossen werden?
- MechIng123
- Grünschnabel

- Beiträge: 6
- Registriert: Mo 18. Mai 2020, 11:51
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Kannst Du die Datentabelle als CSV ausgeben und die Datei hier in Code-Tags hineinpasten? Müssen ja nicht die korrekten Werte sein. R Code lässt sich ganz gut in Foren kommunizieren.
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Hallo,
hier mein Datensatz. x1, x2, x3 sind die Einflussgrößen und y1 ist die Zielgröße.
hier mein Datensatz. x1, x2, x3 sind die Einflussgrößen und y1 ist die Zielgröße.
- Code: Alles auswählen
x1 x2 x3 y1
0.5 0.1 1 1.43
0.5 0.1 2 1.21
0.5 0.1 3 1.19
0.5 0.1 5 1.24
0.5 0.25 1 1.56
0.5 0.25 2 1.27
0.5 0.25 3 1.27
0.5 0.25 5 1.34
0.5 0.5 1 1.24
0.5 0.5 2 1.3
0.5 0.5 3 1.43
0.5 0.5 5 1.28
0.5 1 1 1.53
0.5 1 2 1.47
0.5 1 3 1.35
0.5 1 5 1.43
1 0.1 1 1.69
1 0.1 2 1.2
1 0.1 3 1.28
1 0.1 5 1.23
1 0.25 1 1.67
1 0.25 2 1.39
1 0.25 3 1.4
1 0.25 5 1.42
1 0.5 1 1.67
1 0.5 2 1.48
1 0.5 3 1.41
1 0.5 5 1.56
1 1 1 1.65
1 1 2 1.65
1 1 3 1.57
1 1 5 1.6
1.5 0.1 1 1.88
1.5 0.1 2 1.23
1.5 0.1 3 1.21
1.5 0.1 5 1.25
1.5 0.25 1 2.2
1.5 0.25 2 1.56
1.5 0.25 3 1.6
1.5 0.25 5 1.5
1.5 0.5 1 2.11
1.5 0.5 2 1.68
1.5 0.5 3 1.62
1.5 0.5 5 1.68
1.5 1 1 1.79
1.5 1 2 2.04
1.5 1 3 1.86
1.5 1 5 1.86
2 0.1 1 1.99
2 0.1 2 1.21
2 0.1 3 1.27
2 0.1 5 1.35
2 0.25 1 2.04
2 0.25 2 1.63
2 0.25 3 1.42
2 0.25 5 1.54
2 0.5 1 1.99
2 0.5 2 1.83
2 0.5 3 1.82
2 0.5 5 2.1
2 1 1 2.05
2 1 2 1.9
2 1 3 1.8
2 1 5 1.9
- MechIng123
- Grünschnabel

- Beiträge: 6
- Registriert: Mo 18. Mai 2020, 11:51
- Danke gegeben: 2
- Danke bekommen: 0 mal in 0 Post
Re: 4^3 vollfaktoriellen Versuchsplan auswerten
Und sollen die Prädiktoren als metrische Werte oder als nominale Faktoren ins Modell eingehen? Ist x = 2 doppelt soviel wie x = 1 oder soll für beide Stufen ein Koeffizient geschätzt werden?
Hier mal Code für den Fall metrischer Prädiktoren:
Das liefert eine sehr ordentliche Residuenverteilung, alle Prädiktoren sind signifikant, erklärte Varianz 57% für folgendes Modell:
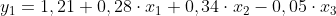
LG,
Bernhard
Hier mal Code für den Fall metrischer Prädiktoren:
- Code: Alles auswählen
# Daten einlesen und der Tabelle den Namen stream zuweisen
stream <- read.table(header = TRUE,
text = "x1 x2 x3 y1
0.5 0.1 1 1.43
0.5 0.1 2 1.21
0.5 0.1 3 1.19
0.5 0.1 5 1.24
0.5 0.25 1 1.56
0.5 0.25 2 1.27
0.5 0.25 3 1.27
0.5 0.25 5 1.34
0.5 0.5 1 1.24
0.5 0.5 2 1.3
0.5 0.5 3 1.43
0.5 0.5 5 1.28
0.5 1 1 1.53
0.5 1 2 1.47
0.5 1 3 1.35
0.5 1 5 1.43
1 0.1 1 1.69
1 0.1 2 1.2
1 0.1 3 1.28
1 0.1 5 1.23
1 0.25 1 1.67
1 0.25 2 1.39
1 0.25 3 1.4
1 0.25 5 1.42
1 0.5 1 1.67
1 0.5 2 1.48
1 0.5 3 1.41
1 0.5 5 1.56
1 1 1 1.65
1 1 2 1.65
1 1 3 1.57
1 1 5 1.6
1.5 0.1 1 1.88
1.5 0.1 2 1.23
1.5 0.1 3 1.21
1.5 0.1 5 1.25
1.5 0.25 1 2.2
1.5 0.25 2 1.56
1.5 0.25 3 1.6
1.5 0.25 5 1.5
1.5 0.5 1 2.11
1.5 0.5 2 1.68
1.5 0.5 3 1.62
1.5 0.5 5 1.68
1.5 1 1 1.79
1.5 1 2 2.04
1.5 1 3 1.86
1.5 1 5 1.86
2 0.1 1 1.99
2 0.1 2 1.21
2 0.1 3 1.27
2 0.1 5 1.35
2 0.25 1 2.04
2 0.25 2 1.63
2 0.25 3 1.42
2 0.25 5 1.54
2 0.5 1 1.99
2 0.5 2 1.83
2 0.5 3 1.82
2 0.5 5 2.1
2 1 1 2.05
2 1 2 1.9
2 1 3 1.8
2 1 5 1.9")
# zur Plausibilitätsprüfung Zusammenfassung der eingelesenen Daten anschauen
summary(stream)
# OLS-Regression mit metrischen Prädiktoren:
mod1 <- lm(y1 ~ x1 +x2 + x3, data = stream)
# 4 diagnostische Plots zu dem Modell (sehen nicht schlecht aus)
plot(mod1)
# Numerische Beschreibung und Analyse des Modells:
summary(mod1)
AIC(mod1)
Das liefert eine sehr ordentliche Residuenverteilung, alle Prädiktoren sind signifikant, erklärte Varianz 57% für folgendes Modell:
- Code: Alles auswählen
> summary(mod1)
Call:
lm(formula = y1 ~ x1 + x2 + x3, data = stream)
Residuals:
Min 1Q Median 3Q Max
-0.48099 -0.10712 -0.01094 0.11079 0.54333
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.21005 0.07867 15.381 < 2e-16 ***
x1 0.27625 0.04189 6.595 1.22e-08 ***
x2 0.34009 0.06854 4.962 6.07e-06 ***
x3 -0.05279 0.01583 -3.334 0.00147 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 0.1873 on 60 degrees of freedom
Multiple R-squared: 0.5691, Adjusted R-squared: 0.5476
F-statistic: 26.41 on 3 and 60 DF, p-value: 5.136e-11
LG,
Bernhard
----
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
`Oh, you can't help that,' said the Cat: `we're all mad here. I'm mad. You're mad.'
`How do you know I'm mad?' said Alice.
`You must be,' said the Cat, `or you wouldn't have come here.'
(Lewis Carol, Alice in Wonderland)
- bele
- Schlaflos in Seattle

- Beiträge: 5944
- Registriert: Do 2. Jun 2011, 23:16
- Danke gegeben: 16
- Danke bekommen: 1405 mal in 1391 Posts
Wer ist online?
Mitglieder in diesem Forum: 0 Mitglieder und 1 Gast


